Rumah >pembangunan bahagian belakang >Tutorial Python >Analisis terperinci Python bagi algoritma carian binari
Analisis terperinci Python bagi algoritma carian binari
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBke hadapan
- 2022-06-28 15:23:462984semak imbas
Artikel ini membawakan anda pengetahuan yang berkaitan tentang python Ia terutamanya mengatur isu yang berkaitan dengan algoritma carian binari, termasuk penerangan algoritma, analisis algoritma, idea algoritma, dsb. Mari kita lihat, harap. ia membantu semua orang.

Pembelajaran yang disyorkan: tutorial video python
1. Penerangan algoritma
Dikotomi adalah satu Kaedah carian yang agak cekap
Ingat kembali permainan kecil teka nombor yang telah anda mainkan sebelum ini Integer positif x kurang daripada 100 diberikan terlebih dahulu, dan anda akan diberi gesaan untuk menilai saiz semasa meneka. proses, dan tanya anda bagaimana Tekanya dengan cepat?
Permainan yang kami mainkan sebelum ini memberi 10 peluang Jika kami mempelajari kaedah carian binari, tidak kira berapa pun nombornya, ia hanya mengambil masa sehingga 7 kali untuk meneka nombor.
2. Analisis algoritma
1.
2. Terdapat keperluan untuk jumlah data.
Jumlah data terlalu kecil untuk sesuai untuk carian binari dan peningkatan kecekapan tidak jelas berbanding dengan traversal langsung.
Carian binari tidak sesuai jika jumlah data terlalu besar, kerana tatasusunan memerlukan ruang storan berterusan Jika jumlah data terlalu besar, ruang memori berterusan untuk menyimpan data berskala besar itu selalunya tidak ditemui . .
3. Idea Algoritma
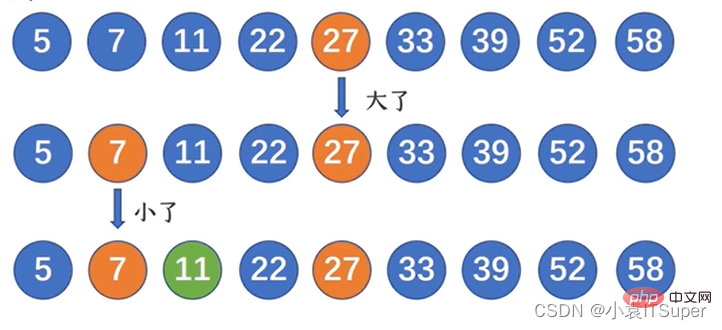
Andaikan terdapat senarai tersusun seperti berikut:
Adakah nombor 11 Dalam senarai ini, apakah nilai indeksnya?
4. Pelaksanaan kod
Pelaksanaan algoritma tulen
Kod pelaksanaan :
arr_list = [5, 7, 11, 22, 27, 33, 39, 52, 58]# 需要查找的数字seek_number = 11# 保存一共查找了几次count = 0# 列表左侧索引left = 0# 列表右侧索引right = len(arr_list) - 1# 当左侧索引小于等于右侧索引时while left arr_list[middle]:
# 左侧索引为中间位置索引+1
left = middle + 1
# 如果查找的数字小于中间位置的数字时
elif seek_number <p>Hasil berjalan: </p><p><img src="https://img.php.cn/upload/article/000/000/067/ab7ca007166584d2196443b3030f239a-4.png" alt="Analisis terperinci Python bagi algoritma carian binari"></p><h2>Pelaksanaan kaedah rekursif</h2><blockquote><p>Satu kiraan pembolehubah ditakrifkan dalam gelung, jika Jika kiraan tidak berubah selepas gelung pertama, ini bermakna input adalah urutan tersusun Pada masa ini, kami terus kembali untuk keluar dari gelung Kerumitan masa pada masa ini ialah O(n)</p></blockquote><p> Kod pelaksanaan: </p><pre class="brush:php;toolbar:false">arr_list = [5, 7, 11, 22, 27, 33, 39, 52, 58]def binary_search(seek_number, left, right):
if left arr_list[middle]:
left = middle + 1
else:
return middle # 进行递归调用
return binary_search(seek_number, left, right)
# 当左侧索引大于右侧索引时,说明没有找到
else:
return -1# 查找的数字seek_number = 11# 列表左侧索引left = 0# 列表右侧索引right = len(arr_list) - 1print("查找的数字:%s,索引为:%s" % (seek_number, binary_search(seek_number, left, right)))Hasil larian:

Pembelajaran yang disyorkan: Tutorial video Python
Atas ialah kandungan terperinci Analisis terperinci Python bagi algoritma carian binari. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!