Apakah pokok binari lengkap dan pokok binari petunjuk? Apakah struktur penyimpanan berurutan mereka?

Dalam artikel lepas, kami mempelajari struktur rantai asas pokok binari dan operasi yang berkaitan dengan pembinaan pokok dan traversal. Hari ini kita belajar beberapa konsep yang berkaitan dengan pokok binari dan bentuk pokok binari yang diubah suai.

Pokok Binari Lengkap

Apakah pokok binari lengkap? Sebelum bercakap tentang pokok binari yang lengkap, mari kita bercakap tentang istilah lain: "pokok binari penuh". Pokok binari seperti yang kami tunjukkan dalam artikel kami sebelum ini ialah "pokok binari penuh". Dalam pokok ini, semua nod mempunyai dua nod anak, tiada nod hanya mempunyai satu nod anak, dan semua nod daun terendah berada pada tahap yang sama Pokok jenis ini dipanggil " "Pokok Binari Penuh", juga dikenali sebagai "Perduaan Sempurna Pokok".

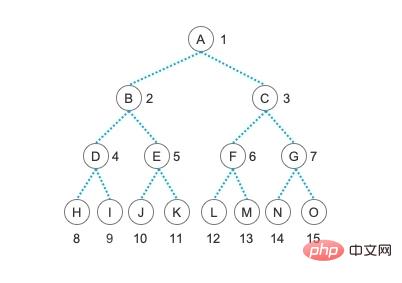
Bukankah ia pokok yang sangat cantik? Ya, pokok binari jenis ini sangat sempurna Ia tidak mempunyai nod tambahan dan tiada nod yang hilang. Walau bagaimanapun, pada hakikatnya, perkara yang sempurna sangat jarang berlaku, dan akan sentiasa ada beberapa kekurangan dalam hidup. Kita cuba untuk tidak membiarkan diri kita terlalu banyak kekurangan, tetapi kita tidak boleh hidup tanpa sebarang kekurangan. Oleh itu, kami membenarkan nod daun muncul pada tahap terendah dan tahap bawah seterusnya, dan nod daun pada tahap terendah tertumpu di bahagian kiri pokok, iaitu, nod daun hanya boleh mempunyai subpokok yang tersisa. pokok sebegitu kurang sedikit Pokok itu dipanggil "pokok binari lengkap". Jangan risau ia tidak sempurna, kerana kehidupan yang sedikit tidak sempurna itu sudah lengkap, jadi "pokok binari lengkap" adalah struktur pokok yang ideal.

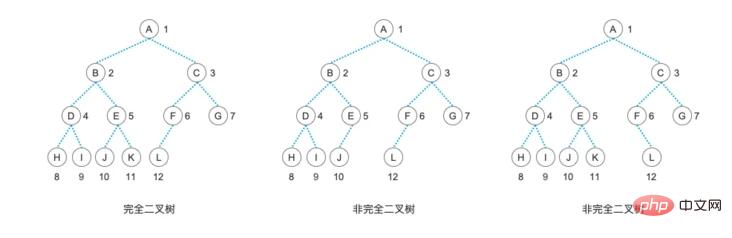
Daripada definisi, kita dapat melihat bahawa "pokok binari penuh" mestilah "pokok binari lengkap", dan nod daun semuanya berada pada satu tahap "lengkap" pokok binari" di mana semua nod mempunyai nod anak kiri dan kanan juga merupakan "pokok binari penuh".

Mengapa kita bercakap tentang "pokok binari penuh" dan "pokok binari lengkap"? Sudah tentu, ia adalah untuk membuka jalan kepada kandungan kami yang seterusnya. Kerana "pokok binari penuh" ialah pokok yang paling sesuai dengan sifat pokok binari. Adakah anda masih ingat lima sifat pokok binari yang diperkenalkan dalam artikel pertama siri pokok? Pada masa itu, kami menggunakan "pokok binari penuh" sebagai contoh untuk menerangkan. Antaranya, Harta 5 adalah asas untuk kita belajar menggunakan struktur berurutan untuk menyimpan pokok binari.

Penyimpanan berjujukan pokok binari

Melalui konsep "pokok binari penuh" dan sifat 5 pokok binari, kita boleh melaksanakan penggunaan tatasusunan untuk menyimpan struktur jujukan.

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];

Saya percaya anda sudah biasa dengannya Dalam artikel sebelumnya, kami menggunakan tatasusunan ini untuk membina pokok rantai, dan tatasusunan ini sebenarnya adalah pokok binari yang disimpan secara linear. Mari kita lihat dengan membandingkan Harta 5 pokok binari.

• Subskrip nod A ialah 1, iaitu akar pokok kita. Nod anaknya ialah B dan C, dan subskrip yang sepadan masing-masing ialah 2 dan 3, iaitu, 1 2 dan 1 2 1.

• Begitu juga, kami memilih satu lagi nod F. Subskripnya ialah 6, jadi subskrip nod anak kirinya ialah 6 2 = 12, sepadan dengan L nod anak kanannya ialah 6 2 1 = 13, sepadan dengan M.

• Sebaliknya, nod induk sesuatu nod ialah i / 2. Mari kita lihat subskrip nod K ialah 11, dan nod induknya ialah 11 / 2. Jika anda menjatuhkan titik perpuluhan, ia adalah kedudukan subskrip 5, iaitu nod E adalah subskrip nod J ialah 10, dan ia nod induk ialah 11/2 Nod ialah 10 / 2, yang juga merupakan nod E dengan indeks 5.

Kini saya rasa semua orang faham cara menggunakan tatasusunan untuk mewakili struktur pokok binari. Lebih-lebih lagi, struktur tatasusunan adalah lebih satu dimensi, yang dapat menggambarkan dengan lebih baik bahawa operasi pokok adalah perwakilan satu dimensi dua dimensi, iaitu penukaran bukan linear kepada linear, supaya kita boleh mengendalikannya dengan mudah. data.

Untuk struktur storan berjujukan, iaitu traversal elemen tatasusunan, bentuk prapesanan, pesanan tengah, pesanan pasca dan susunan lapisan juga boleh digunakan. Walau bagaimanapun, kaedah traversal ini perlu dilalui mengikut Harta 5 pokok binari. Tetapi yang lebih penting, selagi anda memberi saya subskrip, melalui sifat pokok binari, kita boleh dengan mudah mengetahui kedudukan nod bawahan dan nod atasannya, dan kita boleh mendapatkan maklumat nod ini dengan cepat. Ciri utama ini tidak tersedia dalam pokok binari berstruktur rantai.

Bagaimana jika apa yang kita ingin simpan bukan "pokok binari penuh"? Walaupun ia bukan pokok binari yang lengkap, anda hanya perlu menetapkan nod yang sepadan kepada nilai nol. Contohnya:

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

Graf pokok binari yang sepadan dengan struktur pokok ini adalah seperti ini:

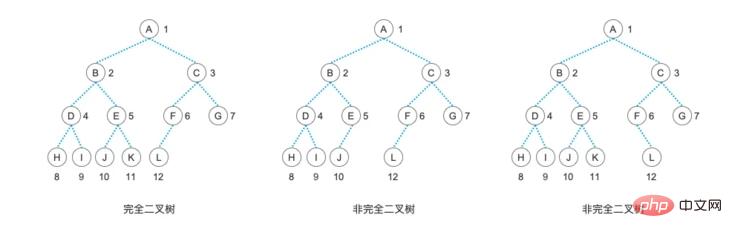
Kemudian dalam kaedah membina rantai pokok, kita Hanya perlu menambah satu lagi penghakiman. Kami boleh menjana pokok binari berantai dengan cepat melalui pokok binari yang disimpan secara berurutan, yang akan memudahkan operasi kami yang seterusnya.

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

Pokok Perduaan Petunjuk

Satu pautan dalam satu lagi, mari kita bincangkan tentang "Pokok Perduaan Petunjuk" seterusnya. Apa ini?

从上面的学习中，我们知道了”满二叉树“和”完全二叉树“。但是这种结构都是非常理想的树结构，不过真实的情况可能大部分都是”理想很丰满，现实很骨感“。很多树并不能形成那样的完全二叉树的形式，更别提”满二叉树“了。而树的遍历又经常会使用栈或者队列来实现，这两种遍历方式基本都是线性的，也就是最好情况下也是 O(n) 的时间复杂度。那么，有没有什么更快一点的方式来提高遍历的效率呢？

我们这样来尝试一下：

• 如果树的叶子结点的左孩子结点为空，就让它指向前驱（上级）结点

• 如果树的叶子结点的右孩子结点为空，就让它指向后继结点

这样有什么好处呢？我们可以避免掉大范围的递归操作，从而加快树的遍历速度。在整个算法中，它并没有什么优势，因为我们需要将一颗树进行线索化，也就是去改变它的叶子结点的左右孩子的指向，这也是一次遍历。但是，如果你的操作是经常需要遍历，而且是来回的多次遍历，那么它的整体性能是要强于普通二叉树的遍历的。因为在一次线索化之后，它的遍历就是在快速的查找叶子结点的基础上进行普通的线性遍历操作，而不是递归操作。

对于线索二叉树来说，我们需要改变树的结点存储数据结构。

// 线索二叉树结点
class TBTNode
{
    public $data;
    public $lTag = 0;
    public $rTag = 0;
    public $lChild;
    public $rChild;
}

我们增加了两个标志位，当 $lTag 或 $rTag 为 1 时，$lChild 或 $rChild 分别指向前驱或后继结点。这样在最后的遍历时，我们就可以快速地通过这个 tag 标志位分辨出结点的指向状态。

然后我们先简单地建立一颗树。使用上一节中的那个示例。

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

$tree = CreateBiTree($treeList, 1);

接下来就是最重要的线索化过程，我们可以建立前序、中序、后序的线索二叉树。对应的，在最后的线索二叉树遍历时获得的结果也将是这三种遍历方式所对应的结果。在这里，我们学习最普遍的也是最经典的”中序线索二叉树“。所以，我们以中序遍历的形式将这颗树线索化。

// 线索化
function InThread(?TBTNode $p, ?TBTNode &$pre)
{
    if ($p) {
        // 递归，左子树线索化
        InThread($p->lChild, $pre);

        if (!$p->lChild) {
            // 建立当前结点的前驱线索
            $p->lChild = $pre;
            $p->lTag = 1;
        }
        if ($pre && !$pre->rChild) {
            // 建立当前结点的后继线索
            $pre->rChild = $p;
            $pre->rTag = 1;
        }
        $pre = $p; // $pre 指向当前的 $p ，作为 $p 将要指向的下一个结点的前驱结点指示指针
        $p = $p->rChild; // $p 指向一个新结点，此时 $pre 和 $p 分别指向的结点形成了一个前驱后继对，为下一次线索化做准备
        
        // 递归，右子树线索化
        InThread($p, $pre);
    }
}

// 创建线索二叉树
function createInThread(TBTNode $root)
{
    $pre = null; // 前驱结点指针
    if($root){
        InThread($root, $pre);
        $pre->rChild = null; // 非空二叉树，线索化
        $pre->rTag = 1; // 后处理中序最后一个结点
    }
}

createInThread($tree);

var_dump($tree);
// object(TBTNode)#1 (5) {
//     ["data"]=>
//     string(1) "A"
//     ["lTag"]=>
//     int(0)
//     ["rTag"]=>
//     int(0)
//     ["lChild"]=>
//     object(TBTNode)#2 (5) {
//       ["data"]=>
//       string(1) "B"
//       ["lTag"]=>
//       int(0)
//       ["rTag"]=>
//       int(0)
//       ["lChild"]=>
//       object(TBTNode)#3 (5) {
//         ["data"]=>
//         string(1) "D"
//         ["lTag"]=>
//         int(1)
//         ["rTag"]=>
//         int(1)
//         ["lChild"]=>
//         NULL
//         ["rChild"]=>
//         *RECURSION*
//       }
//       ……

关于算法的具体步骤在注释中已经写得很详细了。一句话总结就是在中序遍历的过程中，根据结点的信息来确定它的左右孩子的形式，如果有左右孩子就继续，如果没有任一一个孩子的话，就将左右结点指向前驱或者后继。建立之后的线索二叉树就如图所示：

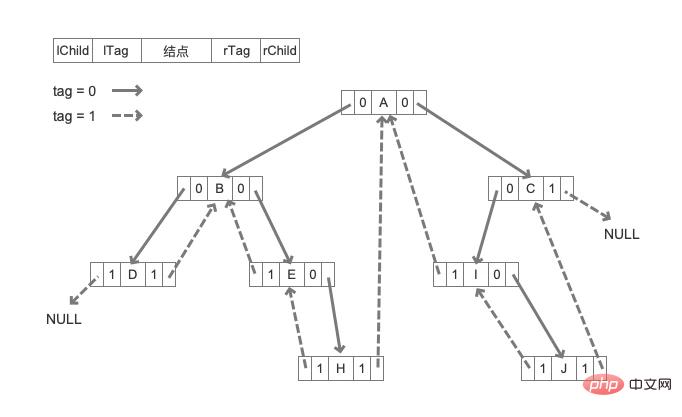
最后就是遍历了。我们需要的是能够快速地获得最左叶子结点的信息，然后就是下一跳的信息，这时，线索的威力就发挥出来了。

// 以 $p 为根的中序线索二叉树中，中序序列下的第一个结点，也就是最左边那个结点
function First(?TBTNode $p){
    while($p->lTag == 0){
        $p = $p->lChild; // 最左下结点（不一定是叶子结点）
    }
    return $p;
}

// 在中序二叉树中，结点 $p 在中序下的后继结点
function NextNode(?TBTNode $p){
    if($p->rTag == 0){
        return First($p->rChild);
    }else{
        return $p->rChild; // 如果 rTag == 1 ，直接返回后继线索
    }
}

// 在中序线索二叉树上进行中序遍历
function Inorder(TBTNode $root){
    //     第一个结点      结点不为空    下一个结点
    for($p = First($root);$p;$p=NextNode($p)){
        echo $p->data, ',';
    }
}

Inorder($tree); // D,B,E,H,A,I,J,C,

当遇到 $lTag 不为 0 的结点时，这个结点就是最左的那个结点了，如果这个不为空的话，【输出】它。接着我们获得下一跳的结点，也就是判断这个结点的右孩子 $rTag 标志，如果是为 0 的，也就是它还有右孩子，【输出】后向下查找，直到找到一个 $rTag 也为 1 的结点，直接返回这个结点的后继，也就是中序遍历的中间那个结点，【输出】它。

最后输出的顺序是不是和我们中序遍历的结果一样呢？注意看代码，在遍历中序线索二叉树的时候，我们没有用一个递归吧，全部是使用的 while() 和 for() 就完成了对这个线索二叉树的遍历。

总结

坚持到现在不容易，不能再小看数据结构了吧？现在还只是树，我们的图都还没开始呢！当然，也不要害怕，一步一步的学，慢慢掌握，不要幻想一口气吃成个胖子。写完这篇文章我也不可能马上就手写出一个中序的线索二叉树来的。大家还是以理解原理为主，如果说真能手写的话，那也是为了面试而去背的或者是为了考研而准备的。这样的小同学在面试中我反而要更多问一些其它的问题，毕竟临时抱佛脚的准备远不如深入理解带来的感悟更能打动人！

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.3完全二叉树、线索二叉树及树的顺序存储结构.php

推荐学习：php视频教程

Atas ialah kandungan terperinci Apakah pokok binari lengkap dan pokok binari petunjuk? Apakah struktur penyimpanan berurutan mereka?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!