Apakah kaedah pengisihan dalam bahasa C?

Kaedah pengisihan bahasa C termasuk: 1. Isih pemilihan mudah, algoritma pengisihan berdasarkan kerumitan masa O(n2); 2. Isih buih; , algoritma pengisihan berdasarkan operasi gabungan 6. Isih cepat, jenis kaedah bahagi dan takluk 7. Isih timbunan, dsb.

Persekitaran pengendalian tutorial ini: sistem Windows 7, versi C 17, komputer Dell G3.

1. Isih pilihan - isihan pilihan ringkas

Isih pilihan ialah algoritma pengisihan yang paling mudah berdasarkan kerumitan masa O(n2) Idea asasnya ialah bermula dari kedudukan i=0 hingga i= n-1 mencari nilai minimum (terbesar) dari kedudukan i ke kedudukan n-1 melalui gelung dalam setiap kali.

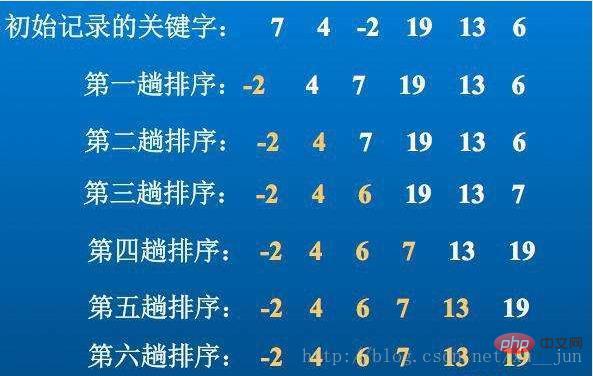
Pelaksanaan algoritma:

void selectSort(int arr[], int n)
{    int i, j , minValue, tmp;    for(i = 0; i < n-1; i++)
    {
        minValue = i;        for(j = i + 1; j < n; j++)
        {            if(arr[minValue] > arr[j])
            {
                minValue = j;
            }
        }        if(minValue != i)
        {
            tmp = arr[i];
            arr[i] = arr[minValue];
            arr[minValue] = tmp;
        }
    }
}void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");
}void main()
{    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    selectSort(arr, 10);
    printArray(arr, 10);    return;
}

Seperti yang ditunjukkan dalam pelaksanaan, kerumitan pengisihan pemilihan mudah ditetapkan pada O(n2), dan setiap dalaman loop finds Cari nilai minimum dalam urutan yang tidak diisih, dan kemudian tukarkannya dengan data semasa. Oleh kerana pemilihan mengisih dengan mencari nilai maksimum, bilangan gelung hampir tetap Kaedah pengoptimuman adalah untuk mencari nilai maksimum dan minimum pada masa yang sama setiap gelung Ini boleh mengurangkan bilangan gelung kepada (n/2 ), cuma tambah dalam gelung Untuk merekodkan nilai maksimum, prinsipnya adalah sama, dan artikel ini tidak akan lagi melaksanakan kaedah ini.

2. Isih gelembung

Isih gelembung berada dalam set tatasusunan yang perlu diisih Apabila susunan pasangan data bertentangan dengan susunan yang diperlukan, data ditukar supaya data yang lebih besar dialihkan kembali , setiap operasi pengisihan meletakkan nombor terbesar pada kedudukan terakhir, seperti berikut:

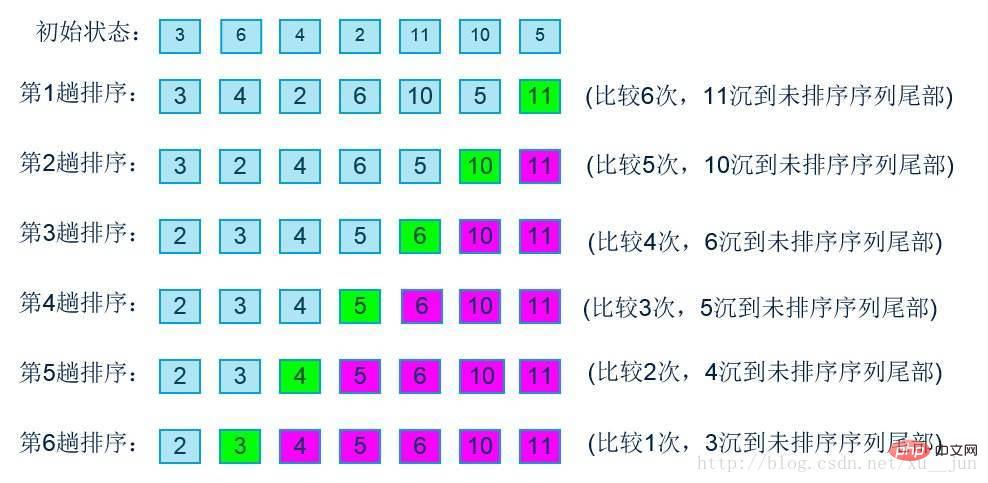
Pelaksanaan algoritma:

void bubbleSort(int arr[], int n)
{    int i, j, tmp;    for(i = 0; i < n - 1; i++)
    {        for(j = 1; j < n; j++)
        {            if(arr[j] < arr[j - 1])
            {
                tmp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = tmp;
            }
        }
    }
}void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");
}void main()
{    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    bubbleSort(arr, 10);
    printArray(arr, 10);    return;
}

Di atas adalah yang paling mudah Dalam pelaksanaan Algoritma boleh dioptimumkan daripada sekurang-kurangnya dua mata:
1) Untuk gelung luar, jika urutan semasa sudah teratur, iaitu, tiada pertukaran akan dilakukan, seterusnya gelung harus dilonjak keluar terus.
2) Apabila nilai maksimum selepas gelung dalam sudah teratur, gelung tidak perlu dilakukan lagi.

Pelaksanaan kod yang dioptimumkan:

void bubbleSort_1(int arr[], int n)
{    int i, nflag, tmp;    do
    {
        nflag = 0;        for(i = 0; i < n - 1; i++)
        {            if(arr[i] > arr[i + 1])
            {
                tmp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = tmp;
                nflag = i + 1;
            }
        }
        n = nflag;
    }while(nflag);
}

Seperti di atas, apabila nflag ialah 0, ini bermakna tiada pertukaran telah berlaku dalam kitaran ini, urutan adalah teratur dan tidak perlu gelung sekali lagi. Jika nflag>0, ia direkodkan Pada kedudukan di mana pertukaran terakhir berlaku, urutan selepas kedudukan ini semuanya teratur dan kitaran tidak akan diteruskan lagi.

3. Isih Sisipan - Isih Sisipan Mudah

Isih sisipan adalah untuk memasukkan rekod ke dalam urutan yang telah dipesan dan mendapatkan urutan tertib dengan elemen baharu tambah satu Elemen pertama dianggap sebagai urutan tertib Bermula dari elemen kedua, urutan tertib yang lengkap diperoleh dengan memasukkan satu demi satu Proses penyisipan adalah seperti berikut:

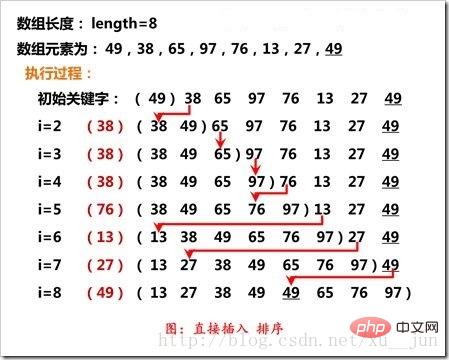
. Seperti yang ditunjukkan dalam rajah, Dalam isihan sisipan, elemen ke-i dibandingkan dengan elemen sebelumnya yang bersebelahan Jika susunan isihan diterbalikkan, elemen ke-i ditukar dengan elemen sebelumnya, dan gelung diteruskan sehingga yang sesuai. kedudukan dicapai.

Pelaksanaan algoritma:

void insertSort(int arr[], int n)
{    int i, j, tmp;    for(i = 1; i < n; i++)
    {        for(j = i; j > 0; j--)
        {            if(arr[j] < arr[j-1])
            {
                tmp = arr[j];
                arr[j] = arr[j-1];
                arr[j-1] = tmp;
            }            else
            {                break;
            }
        }
    }    return;
}void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");    return;
}void main()
{    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    insertSort(arr, 10);
    printArray(arr, 10);    return;
}

Seperti yang dinyatakan di atas, pengisihan pemilihan sentiasa algoritma O(n2) tetap dalam apa jua keadaan dan algoritma sisipan juga merupakan algoritma O(n2). , tetapi boleh dilihat bahawa apabila ia sudah dipesan, sisipan boleh melompat keluar dari gelung secara langsung Dalam kes yang melampau (disusun sepenuhnya) isihan sisipan boleh menjadi algoritma O(n). Walau bagaimanapun, dalam kes ujian yang benar-benar tidak teratur, berbanding dengan jenis pemilihan dalam artikel ini, didapati bahawa jenis sisipan berjalan lebih lama daripada jenis pemilihan dalam kes jujukan yang sama. Ini kerana setiap gelung luar daripada isihan pemilihan hanya sepadan dengan kebanyakan Nilai yang dipilih ditukar, manakala pengisihan sisipan memerlukan pertukaran berterusan dengan elemen bersebelahan untuk mencari kedudukan yang sesuai bagi pertukaran juga mempengaruhi masa berjalan, jadi titik ini dioptimumkan di bawah:

Selepas pengoptimuman:

void insertSort_1(int arr[], int n)
{    int i, j, tmp, elem;    for(i = 1; i < n; i++)
    {
        elem = arr[i];        for(j = i; j > 0; j--)
        {            if(elem < arr[j-1])
            {
                arr[j] = arr[j-1];
            }            else
            {                break;
            }
        }
        arr[j] = elem;
    }    return;
}

Kod yang dioptimumkan menyimpan cache nilai yang perlu dimasukkan, menggerakkan elemen selepas kedudukan sisipan ke belakang dengan satu dan menukar tiga tugasan pertukaran kepada satu tugasan untuk mengurangkan masa pelaksanaan.

4. Isih sisipan - Isih bukit

Idea asas Isih Bukit ialah terlebih dahulu mengambil integer d1 kurang daripada n sebagai kenaikan pertama dan kumpulkan semua elemen. Semua rekod yang jaraknya adalah gandaan d1 diletakkan dalam kumpulan yang sama. Mula-mula lakukan pengasingan sisipan terus dalam setiap kumpulan kemudian, ambil kenaikan kedua d2

1) Pengisihan sisipan dilakukan pada item yang hampir telah diisih. kecekapan adalah tinggi, iaitu kecekapan pengisihan linear boleh dicapai.

2)但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

排序过程如下：

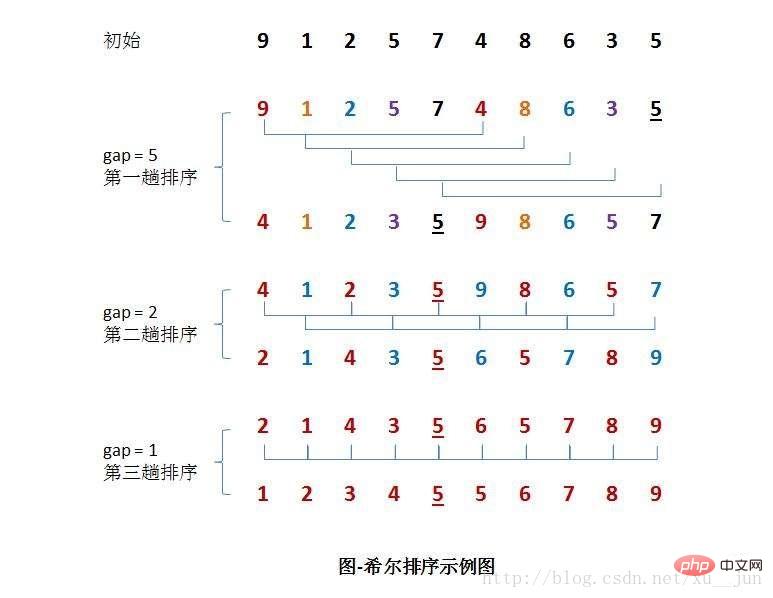
算法实现：基于一种简单的增量分组方式｛n/2,n/4,n/8……,1｝

void shellSort(int arr[], int n)
{    int i, j, elem;    int k = n/2;    while(k>=1)
    {        for(i = k; i < n; i ++)
        {
            elem = arr[i];            for(j = i; j >= k; j-=k)
            {                if(elem < arr[j-k])
                {
                    arr[j] = arr[j-k];
                }                else
                {                    break;
                }
            }
            arr[j] = elem;
        }
        k = k/2;
    }
}void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");    return;
}void main()
{    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    shellSort(arr, 10);
    printArray(arr, 10);    return;
}

5.归并排序

归并排序是基于归并操作的一种排序算法，归并操作的原理就是将一组有序的子序列合并成一个完整的有序序列，即首先需要把一个序列分成多个有序的子序列，通过分解到每个子序列只有一个元素时，每个子序列都是有序的，在通过归并各个子序列得到一个完整的序列。

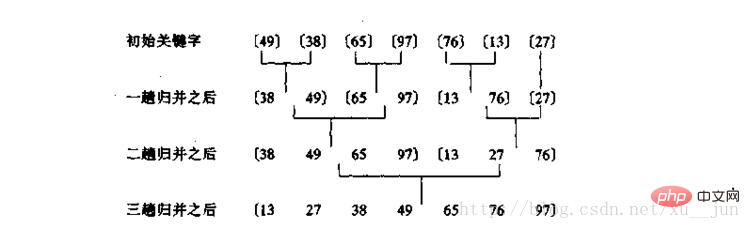
合并过程：

把序列中每个单独元素看作一个有序序列，每两个单独序列归并为一个具有两个元素的有序序列，每两个有两个元素的序列归并为一个四个元素的序列依次类推。两个序列归并为一个序列的方式：因为两个子序列都是有序的（假设由小到大），所有每个子序列最左边都是序列中最小的值，整个序列最小值只需要比较两个序列最左边的值，所以归并的过程不停取子序列最左边值中的最小值放到新的序列中，两个子序列值取完后就得到一个有序的完整序列。

归并的算法实现：

void merge(int arr[], int l, int mid, int r)
{    int len,i, pl, pr;    int *tmp = NULL;

    len = r - l + 1;
    tmp = (int*)malloc(len * sizeof(int));  //申请存放完整序列内存
    memset(tmp, 0x0, len * sizeof(int));

    pl = l;
    pr = mid + 1;
    i  = 0;    while(pl <= mid && pr <= r)  //两个子序列都有值，比较最小值
    {        if(arr[pl] < arr[pr])
        { 
            tmp[i++] = arr[pl++];
        }        else
        {
            tmp[i++] = arr[pr++];
        }
    }    while(pl <= mid)        //左边子序列还有值，直接拷贝到新序列中
    {
        tmp[i++] = arr[pl++];
    }    while(pr <= r)      //右边子序列还有值
    {
        tmp[i++] = arr[pr++];
    }    for(i = 0; i < len; i++)
    {
        arr[i+l] = tmp[i];
    }    free(tmp);    return;
}

归并的迭代算法：

迭代算法如上面所说，从单个元素开始合并，子序列长度不停增加直到得到一个长度为n的完整序列。

#include<stdio.h>#include<stdlib.h>#include<string.h>void merge(int arr[], int l, int mid, int r)
{    int len,i, pl, pr;    int *tmp = NULL;

    len = r - l + 1;
    tmp = (int*)malloc(len * sizeof(int));  //申请存放完整序列内存
    memset(tmp, 0x0, len * sizeof(int));

    pl = l;
    pr = mid + 1;
    i  = 0;    while(pl <= mid && pr <= r)  //两个子序列都有值，比较最小值
    {        if(arr[pl] < arr[pr])
        {

            tmp[i++] = arr[pl++];
        }        else
        {
            tmp[i++] = arr[pr++];
        }
    }    while(pl <= mid)        //左边子序列还有值，直接拷贝到新序列中
    {
        tmp[i++] = arr[pl++];
    }    while(pr <= r)      //右边子序列还有值
    {
        tmp[i++] = arr[pr++];
    }    for(i = 0; i < len; i++)
    {
        arr[i+l] = tmp[i];
    }    free(tmp);    return;

}int min(int x, int y)
{    return (x > y)? y : x;
}/*
归并完成的条件是得到子序列长度等于n，用sz表示当前子序列的长度。从1开始每次翻倍直到等于n。根据上面归并的方法，从i=0开始分组，下一组坐标应该i + 2*sz，第i组第一个元素为arr[i],最右边元素应该为arr[i+2*sz -1]，遇到序列最右边元素不够分组的元素个数时应该取n-1,中间的元素为arr[i+sz -1],依次类推进行归并得到完整的序列
*/void mergeSortBu(int arr[], int n)
{    int sz, i, mid,l, r;    for(sz = 1; sz < n; sz+=sz)
    {        for(i = 0; i < n - sz; i += 2*sz)
        {
            l = i;
            r = i + sz + sz;
            mid = i + sz -1;
            merge(arr, l, mid, min(r-1, n-1));
        }
    }    return;
}void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");    return;
}void main()
{    int arr[10] = {2,5,6,4,3,7,9,8,1,0};
    printArray(arr, 10);
    mergeSortBu(arr, 10);
    printArray(arr, 10);    return;
}

另一种是通过递归的方式，递归方式可以理解为至顶向下的操作，即先将完整序列不停分解为子序列，然后在将子序列归并为完整序列。

递归算法实现：

void mergeSort(int arr[], int l, int r)
{    if(l >= r)
    {
        return;
    }    int mid = (l + r)/2;
    mergeSort(arr, l, mid);
    mergeSort(arr, mid+1, r);
    merge(arr, l, mid, r);
    return;
}

对于归并算法大家可以考虑到由于子序列都是有序的，所有如果左边序列的最大值都比右边序列的最小值小，那么整个序列就是有序的，不需要进行merge操作，因此可以在每次merge操作加一个if(arr[mid] > arr[mid+1])判断进行优化,这种优化对于近乎有序的序列非常有效果，不过对于一般的情况会有一次判断的额外开销，可以根据具体情况处理。

6.快速排序

快速排序跟归并排序类似属于分治法的一种，基本思想是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

排序过程如图：

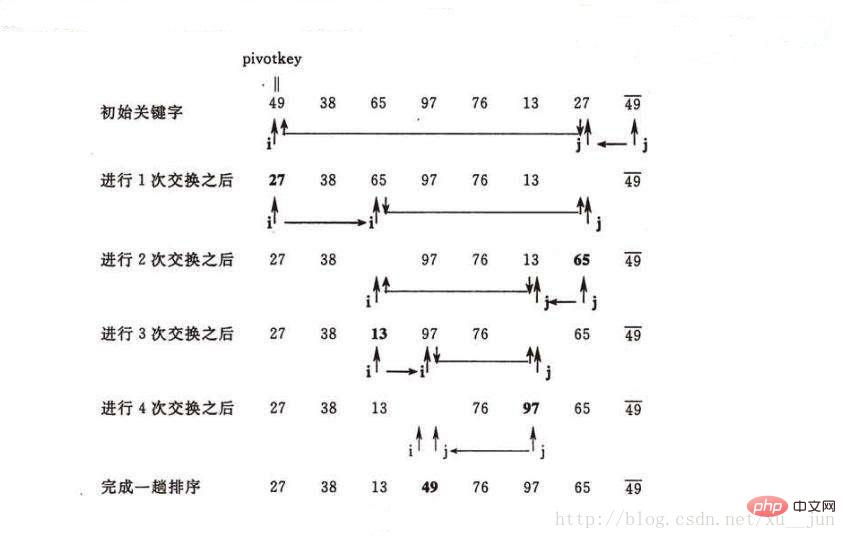
因此，快速排序每次排序将一个序列分为两部分，左边部分都小于等于右边部分，然后在递归对左右两部分进行快速排序直到每部分元素个数为1时则整个序列都是有序的，因此快速排序主要问题在怎样将一个序列分成两部分，其中一部分所有元素都小于另一部分，对于这一块操作我们叫做partition,原理是先选取序列中的一个元素做参考量，比它小的都放在序列左边，比它大的都放在序列右边。

算法实现：

快速排序-单路快排：

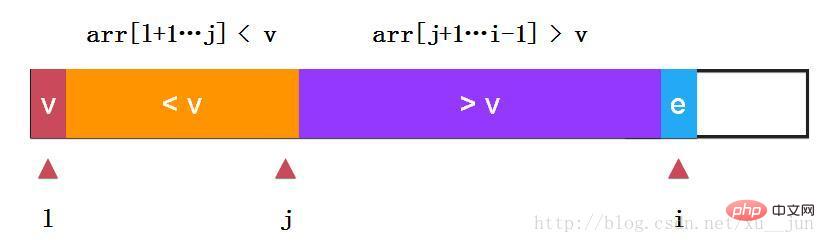
如上：我们选取第一个元素v作为参考量及arr[l],定义j变量为两部分分割哨兵，变量i从l+1开始遍历每个变量，如果当前变量e > v则i++检测下一个元素，如果当前变量e v

代码实现：

#include <stdio.h>void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");    return;
}void swap(int *a, int *b)
{    int tmp;

    tmp = *a;
    *a  = *b;
    *b  = tmp;    return;
}//arr[l+1...j] < arr[l], arr[j+1,..i)>arr[l]static int partition(int arr[], int l, int r)
{    int i, j;
    i = l + 1;
    j = l;    while(i <= r)
    {        if(arr[i] > arr[l])
        {
            i++;
        }        else
        {
            swap(&arr[j + 1], &arr[i]);
            i++;
            j++;
        }
    }
    swap(&arr[l], &arr[j]);    return j;
}static void _quickSort(int arr[], int l, int r)
{    int key;    if(l >= r)
    {        return;
    }
    key = partition(arr, l, r);
    _quickSort(arr, l, key - 1);
    _quickSort(arr, key + 1, r);
}void quickSort(int arr[], int n)
{
    _quickSort(arr, 0, n - 1);    return;
}void main()
{    int arr[10] = {1,5,9,8,7,6,3,4,0,2};

    printArray(arr, 10);
    quickSort(arr, 10);
    printArray(arr, 10);
}

因为有变量i从左到右依次遍历序列元素，所有这种方式叫单路快排，不过细心的同学可以发现我们忽略了考虑e等于v的情况，这种快排方式一大缺点就是对于高重复率的序列即大量e等于v的情况会退化为O（n2）算法，原因在大量e等于v的情况划分情况会如下图两种情况：

解决这种问题的一另种方法：

快速排序-两路快排：

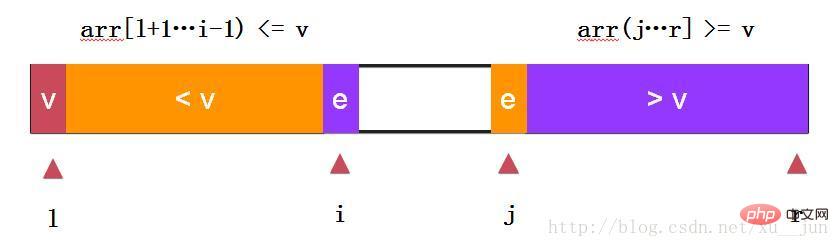
两路快排通过i和j同时向中间遍历元素，e==v的元素分布在左右两个部分，不至于在多重复元素时划分严重失衡。依旧去第一个元素arr[l]为参考量，始终保持arr[l+1….i) =arr[l]原则.

代码实现：

//arr[l+1....i) <=arr[l], arr(j...r] >=arr[l]static int partition2(int arr[], int l, int r)
{    int i, j;

    i = l + 1 ;
    j = r;    while(i <= j)
    {        while(i <= j && arr[j] > arr[l])         /*注意arr[j] >arr[l] 不是arr[j] >= arr[l]*/
        {
            j--;
        }        while(i <= j && arr[i] < arr[l])
        {
            i++;
        }        if(i < j)
        {
            swap(&arr[i], &arr[j]);
            i++;
            j--;
        }
    }
    swap(&arr[j],&arr[l]);    return j;
}

针对重复元素比较多的情况还有一种实现方式：

快速排序-三路快排：

三路快排是在两路快排的基础上对e==v的情况做单独的处理，对于重复元素非常多的情况优势很大：

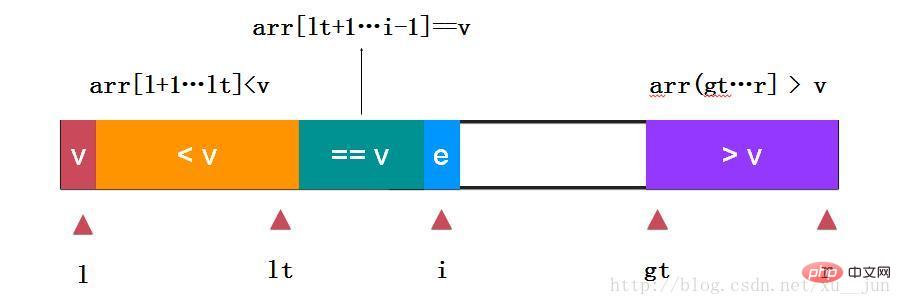
如上：取arr[l]为参考量，定义变量lt为小于v和等于v的分割点，变量i为遍历指针，gt为大于v和未遍历元素分割点，gt指向未遍历元素，边界条件跟个人定义有关本文始终保持arr[l+1…lt] v的状态。

代码实现：

#include <stdio.h>void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");    return;
}
void swap(int *a, int *b)
{    int tmp;

    tmp = *a;    *a  = *b;    *b  = tmp;    return;
}

static void _quickSort3(int arr [ ],int l,int r)
{    int i, lt, gt;    if(l >= r)
    {        return;
    }
    i = l + 1;    lt = l;    gt = r ;    while(i <= gt)
    {        if(arr[i] < arr[l])
        {
            swap(&arr[lt + 1], &arr[i]);            lt ++;
            i++;
        }        else if(arr[i] > arr[l])
        {
            swap(&arr[i], &arr[gt]);            gt--;
        }        else
        {
            i++;
        }
    }

    swap(&arr[l], &arr[gt]);
    _quickSort3(arr, l, lt);
    _quickSort3(arr, gt + 1, r);    return;
}

void quickSort(int arr[], int n)
{
    _quickSort3(arr, 0, n - 1);    return;
}

void main()
{    int arr[10] = {1,5,9,8,7,6,3,4,0,2};

    printArray(arr, 10);
    quickSort(arr, 10);
    printArray(arr, 10);
}

三路快排在重复率比较高的情况下比前两种有较大优势，但就完全随机情况略差于两路快排，可以根据具体情况进行合理选择，另外本文在选取参考值时为了方便一直选择第一个元素为参考值，这种方式对于近乎有序的序列算法会退化到O（n2），因此一般选取参考值可以随机选择参考值或者其他选择参考值的方法然后再与arr[l]交换，依旧可以使用相同的算法。

7.堆排序

堆其实一种树形结构，以二叉堆为例，是一颗完全二叉树（即除最后一层外每个节点都有两个子节点，且非满的二叉树叶节点都在最后一层的左边位置），二叉树满足每个节点都大于等于他的子节点(大顶堆)或者每个节点都小于等于他的子节点（小顶堆），根据堆的定义可以得到堆满足顶点一定是整个序列的最大值（大顶堆）或者最小值（小顶堆）。如下图：

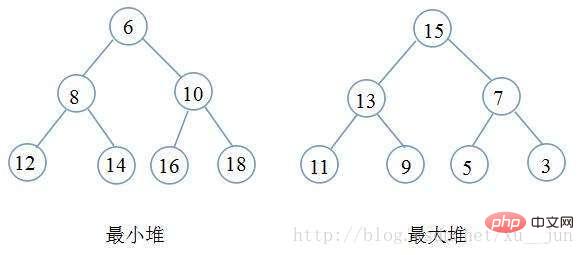
堆排序就是一种基于堆得选择排序，先将需要排序的序列构建成堆，在每次选取堆顶点的最大值和最小值知道完成整个堆的遍历。

用数组表示堆：

二叉堆作为树的一种，通常用结构体表示，为了排序的方便，我们通常使用数组来表示堆，如下图：

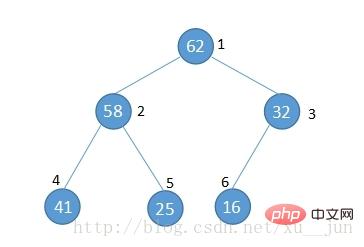
将一个堆按图中的方式按层编号可以得到如下结论：

1）节点的父节点编号满足parent(i) = i/2

2）节点的左孩子编号满足 left child (i) = 2*i

3）节点右孩子满足 right child (i) = 2*i + 1

由于数组编号是从0开始对上面结论修改得到：

parent(i) = (i-1)/2

left child (i) = 2*i + 1

right child (i) = 2*i + 2

堆的两种操作方式：

根据堆的主要性质（父节点大于两个子节点或者小于两个子节点），可以得到堆的两种主要操作方式，以大顶堆为例：

a）如果子节点大于父节点将子节点上移（shift up）

b）如果父节点小于两个子节点中的最大值则父节点下移（shift down）

shift up:

如果往已经建好的堆中添加一个元素，如下图，此时不再满足堆的性质，堆遭到破坏，就需要执行shift up 操作将添加的元素上移调整直到满足堆的性质。

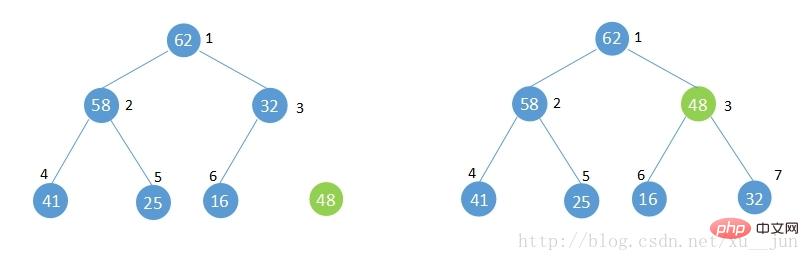
调整堆的方法：

1）7号位新增元素48与其父节点[i/2]=3比较大于父节点的32不满足堆性质，将其与父节点交换。

2）此时新增元素在3号位，再与3号位父节点[i/2]=1比较，小于1号位的62满足堆性质，不再交换，如果此步骤依旧不满足堆性质则重复1步骤直到满足堆的性质或者到根节点。

3）堆调整完成。

代码实现：

代码中基于数组实现，数组下表从0开始，父子节点关系如用数组表示堆

/*parent(i) = (i-1)/2
  left child  (i) = 2*i + 1
  right child (i) = 2*i + 2*/void swap(int *a, int *b)
{    int tmp;

    tmp = *a;    *a  = *b;    *b  = tmp;    return;
}

 void shiftUp(int arr[], int n, int k)
 {    while((k - 1)/2 >= 0 && arr[k] > arr[(k - 1)/2])
    {
        swap(&arr[k], &arr[(k-1)/2]);
        k = (k - 1)/2;
    }    return;
 }

shift down: 

与shift up相反，如果从一个建好的堆中删除一个元素，此时不再满足堆的性质，此时应该怎样来调整堆呢？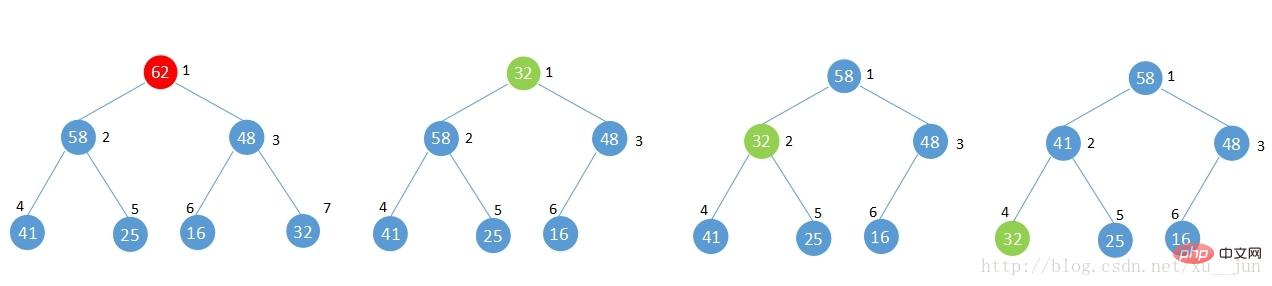

如上图，将堆中根节点元素62删除调整堆的步骤为：

1）将最后一个元素移到删除节点的位置

2）与删除节点两个子节点中较大的子节点比较，如果节点小于较大的子节点，与子节点交换，否则满足堆性质，完成调整。

3）重复步骤2，直到满足堆性质或者已经为叶节点。

4）完成堆调整

代码实现：

 void shiftDown(int arr[], int n, int k)
 {    int j = 0 ;     while(2*k + 1 < n)
     {
        j = 2 *k + 1;    //标记两个子节点较大的节点，初始为左节点
        if (j + 1 < n && arr[j] < arr[j+1])
        {
            j ++;   
        }        if(arr[k] < arr[j])
        {
            swap(&arr[k], &arr[j]);
            k = j;
        }        else
        {            break;
        }
     }     return;
 }

知道了上面两种堆的操作后，堆排序的过程就非常简单了

1）首先将待排序序列建成堆，由于最后一层即叶节点没有子节点所以可以看成满足堆性质的节点，第一个可能出现不满足堆性质的节点在第一个父节点的位置，假设最后一个叶子节点为（n - 1） 则第一个父节点位置为(n-1-1)/2,只需要依次对第一个父节点之前的节点执行shift down操作到根节点后建堆完成。

2）建堆完成后（以大顶堆为例）第一个元素arr[0]必定为序列中最大值，将最大值提取出来（与数组最后一个元素交换），此时堆不再满足堆性质，再对根节点进行shift down操作，依次循环直到根节点，排序完成。

代码实现：

#include/*parent(i) = (i-1)/2
  left child  (i) = 2*i + 1
  right child (i) = 2*i + 2*/void swap(int *a, int *b)
{    int tmp;

    tmp = *a;    *a  = *b;    *b  = tmp;    return;
}

 void shiftUp(int arr[], int n, int k)
 {    while((k - 1)/2 >= 0 && arr[k] > arr[(k - 1)/2])
    {
        swap(&arr[k], &arr[(k-1)/2]);
        k = (k - 1)/2;
    }    return;
 }

 void shiftDown(int arr[], int n, int k)
 {    int j = 0 ;     while(2*k + 1 < n)
     {
        j = 2 *k + 1;        if (j + 1 < n && arr[j] < arr[j+1])
        {
            j ++;   
        }        if(arr[k] < arr[j])
        {
            swap(&arr[k], &arr[j]);
            k = j;
        }        else
        {            break;
        }
     }     return;
 }

 void heapSort(int arr[], int n)
 {    int i = 0;    for(i = (n - 1 -1)/2; i >=0; i--)
    {
        shiftDown(arr, n, i);
    }    for(i = n - 1; i > 0; i--)
    {
        swap(&arr[0], &arr[i]);
        shiftDown(arr, i, 0);
    }    return;
 }

 void printArray(int arr[], int n)
{    int i;    for(i = 0; i < n; i++)
    {        printf("%d ", arr[i]);
    }    printf("\n");    return;
}
 void main()
{    int arr[10] = {1,5,9,8,7,6,3,4,0,2};

    printArray(arr, 10);
    heapSort(arr, 10);
    printArray(arr, 10);
}

推荐教程：《C#》

Atas ialah kandungan terperinci Apakah kaedah pengisihan dalam bahasa C?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!