Penjelasan terperinci tentang traversal pokok binari dan kaedah operasi logik

Pertama sekali, kami masih perlu menjelaskan bahawa kandungan utama yang kami kaji adalah pokok binari, kerana pokok binari adalah aplikasi pokok yang paling tipikal Sama ada peperiksaan atau temu duga, ia mesti diketahui dan mesti -mempelajari kandungan.

Pertama sekali, sebelum mempelajari operasi pokok, kita mesti faham terlebih dahulu bahawa inti operasi pokok ialah "traversal". Kenapa awak cakap macam tu? Tidak seperti susunan dan barisan, struktur pokok sebenarnya tidak lagi berbentuk satu dimensi Ia mempunyai cabang, sudut yang berbeza, dan yang lebih penting, ia mempunyai konsep hierarki.

Perkara dalam ruang satu dimensi ialah "garisan" biasa kami, yang hanya mempunyai panjang tetapi tiada ketinggian, dan panjang ini adalah satu-satunya dimensi Tindanan dan barisan adalah satu dimensi. Pokoknya berbeza kerana konsep hierarki, ia mempunyai "ketinggian", iaitu, ia telah dinaik taraf kepada konsep dua dimensi. Sama seperti kumpulan kata nama yang diperkenalkan dalam artikel sebelum ini, terdapat konsep "ketinggian (kedalaman) pokok".

Selepas dapat melintasi pokok, kita boleh menambah, memadam, mengubah suai dan operasi lain pada nod pokok berdasarkan traversal ini semuanya berdasarkan traversal tentang timbunan dan barisan Sebenarnya, bukankah operasi logik mereka juga bermula dengan traversal? Sama ada ia muncul atau memasuki tindanan atau nyah gilir atau beratur, kita semua berdasarkan peraturan traversal tetap (FILO, FIFO).

Untuk perkara dua dimensi, cara melintasinya adalah perkara utama. Kita hanya perlu melintasi struktur data satu dimensi secara berurutan, tetapi keputusan data dua dimensi tidak boleh hanya dilalui satu demi satu mengikut tertib, kerana terdapat hubungan hierarki antara nod, jadi kita perlu mempertimbangkan arus Jika nod tidak mempunyai nod anak, apakah yang perlu kita lakukan semasa operasi traversal?

Mujurlah kita belajar ilmu ini dengan berdiri di atas bahu gergasi. Ramai warga emas telah merumuskan beberapa kaedah rentas pokok yang sangat mudah untuk kita. Mari kita keluar dari jalan dahulu, mari kita lihat cara membina pokok, iaitu pokok binari yang kami tunjukkan dalam artikel sebelumnya.

Struktur storan berantai pokok binari

Menggunakan storan pokok binari berantai adalah sangat mudah dan sangat visual Kawan, mari letakkan penyimpanan berurutan binari pokok.

class BiTree
{
    public $data;
    public $lChild;
    public $rChild;
}

Sebenarnya, dalam simpanan rantai, kami menggunakan nod satu demi satu untuk menyelamatkan pokok. Setiap nod pokok binari mempunyai medan data, iaitu atribut data. Dua atribut lain boleh dianggap sebagai dua penunjuk bercabang, iaitu nod anak kiri lChild dan nod anak kanan rChild nod ini.

Membandingkan tindanan dan baris gilir, kami hanya menggantikan nod seterusnya dengan nod anak kiri dan kanan Pada dasarnya, ia tidak jauh berbeza dengan tindanan dan baris gilir. Secara terang-terangan, dari perspektif struktur data, kami masih menggunakan storan satu dimensi untuk mewakili konsep dua dimensi, dan transformasi konsep ini memerlukan kami bermula dari perspektif pemahaman konsep.

Pembinaan pokok binari

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i])) {
        return null;
    }
    $t = new BiTree();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

Dengan kaedah yang begitu mudah, kita boleh melengkapkan penubuhan pokok binari berantai. Rakan-rakan, sila lihat dengan teliti, operasi membina pokok yang ringkas ini sebenarnya mengandungi banyak misteri:

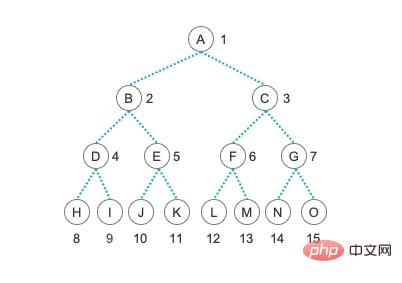
• Kami menggunakan tatasusunan untuk mewakili setiap nod pokok dalam urutan, contohnya, masukkan A dalam jujukan , B, C, D, E... (Kami akan melihatnya sekali lagi dalam simpanan berjujukan pokok)

• Kandungan yang ditetapkan ialah data langganan $i semasa , sila ambil perhatian bahawa kami Operasi rekursif dilakukan apabila memberikan nilai ​​​​kepada kanak-kanak kiri dan kanan

• Apabila mempelajari tindanan, kami mengetahui bahawa "rekursi" ialah jenis tindanan operasi, jadi dalam kod ini, kita membina pokok dalam bentuk tindanan

• Adakah anda perasan i 2 dan i 2 1 setiap kali? Sila semak sifat pokok binari 5

Akhir sekali, kami menguji sama ada kaedah ini berjaya membina struktur pokok yang dipautkan.

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];

$tree = CreateBiTree($treeList, 1);
print_r($tree);

// BiTree Object
// (
//     [data] => A
//     [lChild] => BiTree Object
//         (
//             [data] => B
//             [lChild] => BiTree Object
//                 (
//                     [data] => D
//                     [lChild] => BiTree Object
//                         (
//                             [data] => H
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => I
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//             [rChild] => BiTree Object
//                 (
//                     [data] => E
//                     [lChild] => BiTree Object
//                         (
//                             [data] => J
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => K
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//         )

//     [rChild] => BiTree Object
//         (
//             [data] => C
//             [lChild] => BiTree Object
//                 (
//                     [data] => F
//                     [lChild] => BiTree Object
//                         (
//                             [data] => L
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => M
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//             [rChild] => BiTree Object
//                 (
//                     [data] => G
//                     [lChild] => BiTree Object
//                         (
//                             [data] => N
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                     [rChild] => BiTree Object
//                         (
//                             [data] => O
//                             [lChild] =>
//                             [rChild] =>
//                         )

//                 )

//         )

// )

Kandungan yang dicetak sepatutnya sangat jelas, bukan? Nod A mempunyai dua nod anak kiri dan kanan, iaitu B dan C, nod B mempunyai dua anak kiri dan kanan, masing-masing D dan E, dan seterusnya. Struktur akhir adalah sama seperti struktur rajah pokok binari kami di atas. Di sini, kita juga perlu memberi perhatian kepada fakta bahawa untuk tatasusunan yang diluluskan, kita memberikan elemen pertama, iaitu, data dengan 0 subskrip, kosong, dan membina pokok bermula dari elemen kedua, iaitu elemen dengan 1 subskrip. Ini juga untuk dapat menggunakan Harta 5 pokok binari secara intuitif dan mudah untuk membina pokok ini dengan cepat.

二叉树的遍历

说完二叉树的建树了，其实我们就已经接触到了一种二叉树的遍历形式。注意看我们建树方法中的代码，我们是先给结点的 data 赋值，然后建立这个结点的左、右孩子结点，并为它们赋值后再继续使用同样的操作一路建立完成所有的结点。现在，我们将这个操作反过来，不是建立结点，而是读取这些结点的内容，先读取结点的内容，然后再读取这个结点左右孩子结点的内容，这就是“先序遍历”。

先序遍历

/**
 * 前序遍历
 */
function PreOrderTraverse(?BiTree $t)
{
    if ($t) {
        echo $t->data, ',';
        PreOrderTraverse($t->lChild);
        PreOrderTraverse($t->rChild);
    }
}

PreOrderTraverse($tree);

// A,B,D,H,I,E,J,K,C,F,L,M,G,N,O,

是不是很神奇？就连建树我们竟然也使用的是同一种遍历的方法，可以看出对于二叉树这种复杂的数据结构来说，遍历的重要作用了吧。

大家可以看一个遍历读取出来的结点顺序，貌似和我们输入的顺序不一样呀！没错，先序遍历是通过递归，先按一个方向走到底，当这个结点没有子结点之后，通过递归栈的特性再向上弹出。并且在遍历孩子结点之前先输出当前这个结点的内容。注意，这一句话很重要！所以我们的顺序就是 A,B,D,H ，当 H 没有子结点之后，我们就回到父结点 D 再进入它的右子结点 I ，具体顺序可以参考下图：

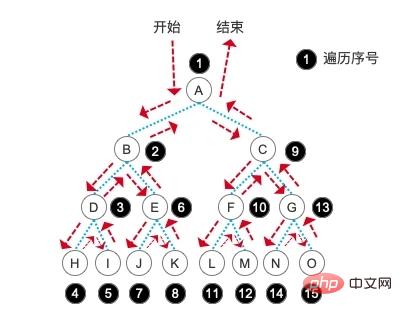
我们代码中的先序遍历和先序建树的结点顺序是完全不一样的，这一点也是要搞清楚的。建树的过程我们根据二叉树的 性质5 直接为它指定了数据下标。而在遍历过程中则是一个结点一个结点的去扫描遍历整颗树的。

中序遍历

顾名思义，中序遍历其实就是在遍历完左孩子结点之后再输出当前这个结点的内容，所以我们只需要微调先序遍历的代码即可。

/**
 * 中序遍历
 */
function InOrderTraverse(?BiTree $t)
{
    if ($t) {
        InOrderTraverse($t->lChild);
        echo $t->data, ',';
        InOrderTraverse($t->rChild);
    }
}

InOrderTraverse($tree);

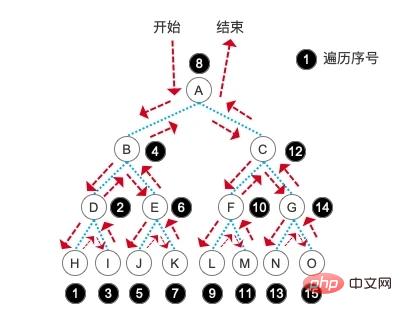
// H,D,I,B,J,E,K,A,L,F,M,C,N,G,O,

中序遍历的步骤就是我们会直接先走到最左边的子结点，当遇到最后一个结点时，输出内容，也就是图中的 H 结点，接着回到它的父结点 D 结点，这时根据中序的原理输出 D ，再进入它的右孩子结点并输出 I 。

D 结点的子树及它本身遍历完成后，返回 D 结点的上级结点 B 结点，输出 B ，然后进入 B 结点的右孩子结点 E 。再次进入到 E 的最左孩子结点 J ，然后参考 D 结点的遍历形式完成整颗树的遍历。具体顺序参考下图：

后序遍历

在学习了先序和中序之后，从名字就可以看出来后序就是在遍历完一个结点的左右孩子之后最后输出这个结点的内容，代码当然也是简单地微调一下就可以了。

/**
 * 后序遍历
 */
function PostOrderTraverse(?BiTree $t)
{
    if ($t) {
        PostOrderTraverse($t->lChild);
        PostOrderTraverse($t->rChild);
        echo $t->data, ',';
    }
}

PostOrderTraverse($tree);

// H,I,D,J,K,E,B,L,M,F,N,O,G,C,A,

具体原理就不详细说明了，相信在学习了先序和中序之后，你一定能马上想明白后序遍历到底是什么意思了。直接上图：

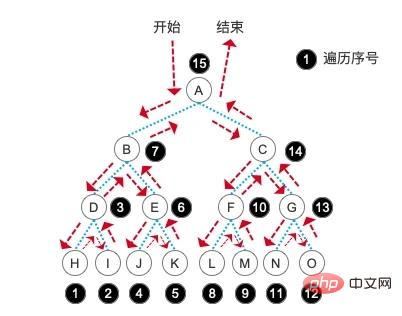
层序遍历

最后，我们要讲的就是层序遍历。既然有“层”这个关键字了，相信大家马上就能联想到，是不是一层一层地去遍历啊！没错，层序遍历就是这个意思，我们按照树的层次，一层一层地输出相应的结点信息。需要注意的，在这里我们会用到队列，而不是栈了。

/**
 * 层序遍历
 */
$q = InitLinkQueue();
function LevelOrderTraverse(?BiTree $t)
{
    global $q;
    if (!$t) {
        return;
    }

    EnLinkQueue($q, $t);
    $node = $q;
    while ($node) {
        $node = DeLinkQueue($q);
        if ($node->lChild) {
            EnLinkQueue($q, $node->lChild);
        }
        if ($node->rChild) {
            EnLinkQueue($q, $node->rChild);
        }
        echo $node->data, ',';
    }
}

LevelOrderTraverse($tree);

// A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,

InitLinkQueue() EnLinkQueue() 、 EnLinkQueue() 这些都是我们之前学习队列的时候所写的对于队列的逻辑操作方法。是不是很开心呀，之前的知识又用上了。层序遍历的核心思想就是运用队列的概念，遇到一个结点，就把这个结点入队，然后判断它是否有子结点，然后相继把子结点入队。

每遍历一个结点，就把队首的结点出队，这样就完成了按树的层次遍历的能力。文字说明还是太抽象，我们还是通过图片来展示这一过程：

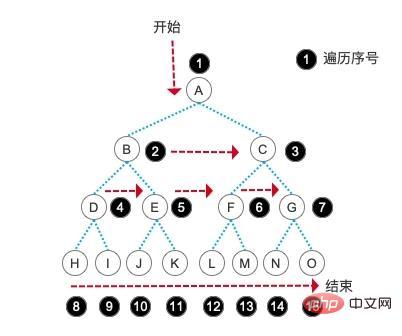
大家有没有发现，层序遍历的输出结果就和我们建树时的数组顺序完全相同了。很好玩吧，所以说代码的世界总是有无穷的乐趣等着我们去发现哦！

总结

今天的内容有没有懵圈？如果懵圈了就多找资料好好研究一下，先序、中序、后序都是利用栈来进行树的结点遍历的，而层序遍历则是利用了队列。一环套一环呀，前面学习的内容都派上用场了吧！不过这只是个开始，在学习图的时候，我们会在深度遍历和广度遍历中再次看到栈和队列的身影，它们可都是亲戚哦。

这四种遍历方式在考试和面试中也是经常出现的，不管是它们的原理还是画图或者是根据图形来写出各种遍历的顺序，都是非常常见的考核内容，所以大家在这篇文章入门的基础上还是要更加深入的去根据一些教材来深入的理解这几种遍历，熟练的掌握它们。

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.2二叉树的遍历及逻辑操作.php

推荐学习：php视频教程

Atas ialah kandungan terperinci Penjelasan terperinci tentang traversal pokok binari dan kaedah operasi logik. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!