Rumah >hujung hadapan web >tutorial js >实现js的双线性插值和双三次插值法
实现js的双线性插值和双三次插值法
- coldplay.xixike hadapan
- 2021-01-25 09:39:233003semak imbas

免费学习推荐:js视频教程
- 介绍
- 双线性插值
- 原理
- 双三次插值法
- 原理
- js实现
介绍
在网页中利用canvas进行绘图时,遇到一个问题,原始的数据分辨率很小,而图片要放大到整个网页,所以需要把数据进行插值放大。学习了双线性插值和三次内插法插值,两种方式实现效果不同,都用js代码实现了一下,下面给大家分享一下
双线性插值
原理
双线性插值即在x和y两个方向上,对数据各进行一次线性插值。
原始数据的矩阵,即一个二维数组,大小为a*b,目标矩阵大小为m*n,m、n比a、b可以大(放大),也可以小(缩小),当然比例也可以不一样, 取决于你插值后的数据需要多大。
基本思想为,遍历目标矩阵的坐标,如x*y这个点,找到这个点在原始矩阵中对应的位置,称为映射点,然后找到这个映射点P在原始矩阵中周围的四个点,然后根据映射点P到这个四个点的x和y方向上的坐标的距离,进行两次线性插值,得到映射点的值即可。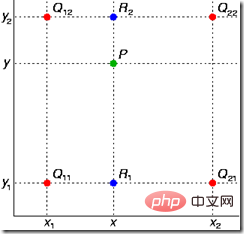
如上图所示,p点为目标矩阵中x*y点在原始矩阵中映射的位置,它周围最近的有Q12,Q11,Q21,Q22四个点,现在x方向进行线性插值,得到R1和R2两个点的值,再在y方向进行一次线性插值,得到P点的值。
注意:用双线性插值放大数据后,如果放大倍数过大,生成图片后发现有着明显的马赛克现象
实现代码参考后面js代码
双三次插值法
原理
双三次插值又称立方卷积插值。三次卷积插值是一种更加复杂的插值方式。该算法利用待采样点周围16个点的灰度值作三次插值,不仅考虑到4 个直接相邻点的灰度影响,而且考虑到各邻点间灰度值变化率的影响。具体的原理可参考下面博客:
参考这里的博客
基本原理就是,先找到目标矩阵中点在源数据矩阵中的映射点P,然后找到P点周围16个点,然后根据P点坐标距离16个点的x和y方向的距离,利用BiCubic函数算出每个点的权重,最后每个点乘以权重后,加起来即可得到P的值。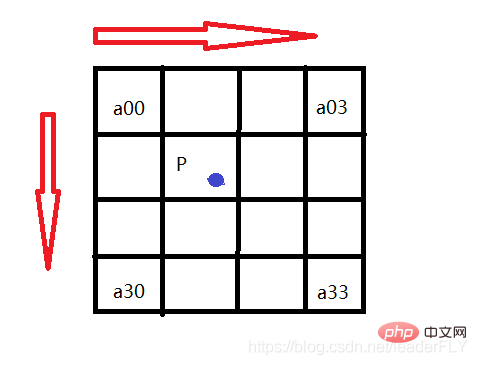
BiCubic函数: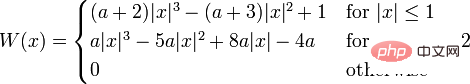
其中,a取-0.5时,BiCubic函数具有如下形状: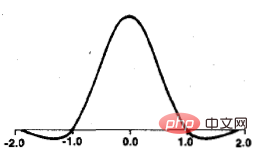
取a=-0.5时,放大的数据挺好,生成的图片非常平滑,也保留了很多细节。
具体为什么要用这个函数,我也没有深入研究,不过利用该方法放大数据后,生成图片效果很好,没有马赛克现象
js实现
/**
* 数据处理工具类(也可以自己直接定义方法,不用class)
*/class DataUtil {
constructor() {}}/**
* 数据插值
* @param w 目标矩阵宽度
* @param h 目标矩阵高度
* @param data 源数据矩阵(二维数组)
* @param type 插值方式,1:双线性插值,2:双三次插值法
*/DataUtil.scaleData = function(w, h, data, type = 2) {
let t1 = new Date().getTime();
let dw = data[0].length;
let dh = data.length;
let resData = new Array(h);
for (let j = 0; j < h; j++) {
let line = new Array(w);
for (let i = 0; i < w; i++) {
let v;
if (type === 2) {
// 双三次插值法
v = DataUtil.cubicInterpolation(w, h, i, j, data);
} else if (type === 1) {
// 双线性插值
v = DataUtil.interpolation(w, h, i, j, data);
} else {
throw new Error('scale data, type not supported(type must be 1 or 2)');
}
line[i] = Math.round(v);
}
resData[j] = line;
}
let t2 = new Date().getTime();
console.log("数据插值耗时:", (t2 - t1));
return resData;}/**
* 双线性插值
* @param sw 目标矩阵的宽度
* @param sh 目标矩阵的高度
* @param x_ 目标矩阵中的x坐标
* @param y_ 目标矩阵中的y坐标
* @param data 源数据矩阵(二维数组)
*/DataUtil.interpolation = function(sw, sh, x_, y_, data) {
let t1 = new Date().getTime();
let w = data[0].length;
let h = data.length;
let x = (x_ + 0.5) * w / sw - 0.5;
let y = (y_ + 0.5) * h / sh - 0.5;
let x1 = Math.floor(x);
let x2 = Math.floor(x + 0.5);
let y1 = Math.floor(y);
let y2 = Math.floor(y + 0.5);
x1 = x1 < 0 ? 0 : x1;
y1 = y1 < 0 ? 0 : y1;
x1 = x1 < w - 1 ? x1 : w - 1;
y1 = y1 < h - 1 ? y1 : h - 1;
x2 = x2 < w - 1 ? x2 : w - 1;
y2 = y2 < h - 1 ? y2 : h - 1;
// 取出原矩阵中对应四个点的值
let f11 = data[y1][x1];
let f21 = data[y1][x2];
let f12 = data[y2][x1];
let f22 = data[y2][x2];
// 计算该点的值
let xm = x - x1;
let ym = y - y1;
let r1 = (1 - xm) * f11 + xm * f21;
let r2 = (1 - xm) * f12 + xm * f22;
let value = (1-ym) * r1 + ym * r2;
return value;}/**
* 双三次插值法
* @param sw 目标矩阵的宽度
* @param sh 目标矩阵的高度
* @param x_ 目标矩阵中的x坐标
* @param y_ 目标矩阵中的y坐标
* @param data 源数据矩阵(二维数组)
*/DataUtil.cubicInterpolation = function (sw, sh, x_, y_, data) {
let w = data[0].length;
let h = data.length;
// 计算缩放后坐标对应源数据上的坐标
let x = x_ * w / sw;
let y = y_ * h / sh;
// 计算x和y方向的最近的4*4的坐标和权重
let wcx = DataUtil.getCubicWeight(x);
let wcy = DataUtil.getCubicWeight(y);
// 权重
let wx = wcx.weight;
let wy = wcy.weight;
// 坐标
let xs = wcx.coordinate;
let ys = wcy.coordinate;
let val = 0;
// 遍历周围4*4的点,根据权重相加
for (let j = 0; j < 4; j++) {
let py = ys[j];
py = py < 0 ? 0 : py;
py = py > h - 1 ? h - 1 : py;
for (let i = 0; i < 4; i++) {
let px = xs[i];
px = px < 0 ? 0 : px;
px = px > w - 1 ? w - 1 : px;
// 该点的值
let dv = data[py][px];
// 该点的权重
let w_x = wx[i];
let w_y = wy[j];
// 根据加权加起来
val += (dv * w_x * w_y);
}
}
return val;}/**
* 双三次插值法中,基于BiCubic基函数,计算源坐标v,最近的4*4的坐标和坐标对应的权重
* @param v 目标矩阵中坐标对应在源矩阵中坐标值
*/DataUtil.getCubicWeight = function (v){
let a = -0.5;
// 取整
let nv = Math.floor(v);
// 坐标差值集合
let xList = new Array(4);
// 坐标集合
let xs = new Array(4);
// 最近的4个坐标差值
xList[0] = nv - v - 1;
xList[1] = nv - v
xList[2] = nv - v + 1;
xList[3] = nv - v + 2;
//
xs[0] = nv - 1;
xs[1] = nv;
xs[2] = nv + 1;
xs[3] = nv + 2;
// 计算权重
let ws = new Array(4);
for (let i = 0; i < 4; i++) {
let val = Math.abs(xList[i]);
let w = 0;
// 基于BiCubic基函数的双三次插值
if (val <= 1) {
w = (a + 2) * val * val * val - (a + 3) * val * val + 1;
} else if (val < 2) {
w = a * val * val * val - 5 * a * val * val + 8 * a * val - 4 * a;
}
ws[i] = w;
}
return {
weight: ws,
coordinate: xs };}
相关免费学习推荐:javascript(视频)
Atas ialah kandungan terperinci 实现js的双线性插值和双三次插值法. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

