java面试中常见的数组题目汇总（二）

1、斐波那契数列

【题目】

大家都知道斐波那契数列，现在要求输入一个整数 n，请你输出斐波那契数列的第 n 项（从 0 开始，第 0 项为 0）。

（视频教程推荐：java课程）

【代码】

package swear2offer.array;


public class FeiBoNaQi {

    /**
     * 大家都知道斐波那契数列，现在要求输入一个整数 n，
     * 请你输出斐波那契数列的第 n 项（从 0 开始，第 0 项为 0）。
     * 0,1,1,2,3,5
     * n<=39
     * */
    public int Fibonacci(int n) {
        if (n == 0) return 0;

        if (n == 1 || n== 2) return 1;

        return Fibonacci(n-1) + Fibonacci(n-2);
    }

    /**
     * 非递归方式，递归的数据结构使用的栈，那就是使用栈的方式
     * */
    public int NoRecursive(int n) {
        if (n>2) {
            int[] a = new int[n+1];
            a[0] = 0;
            a[1] = 1;
            a[2] = 1;

            for (int i=3; i<=n; i++) {
                a[i] = a[i-1] + a[i-2];
            }

            return a[n];
        } else {
            if (n == 0) return 0;
            else return 1;
        }
    }

    public static void main(String[] args) {
        System.out.println(new FeiBoNaQi().Fibonacci(39));
        System.out.println(new FeiBoNaQi().Fibonacci(39));
    }
}

2、矩形覆盖

【题目】

我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形，总共有多少种方法？

比如 n=3 时，2*3 的矩形块有 3 种覆盖方法：

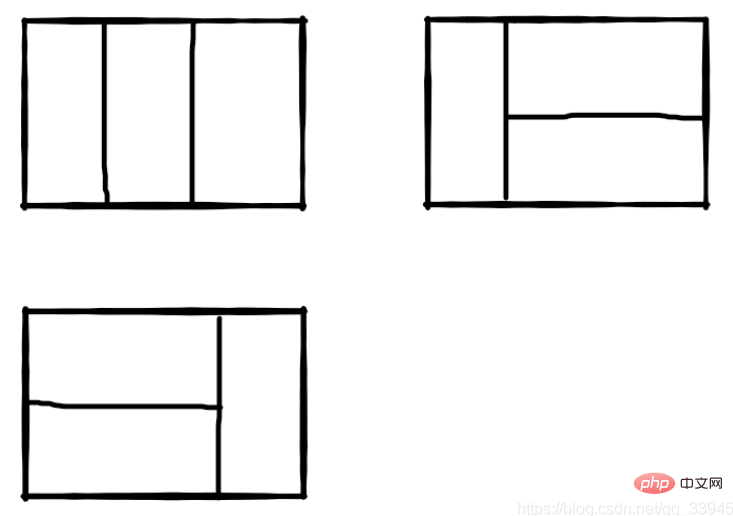
代码：

package swear2offer.array;

public class Rectangle {

    /**
     * f[0] = 0;
     * f[1] = 1;
     * f[2] = 2;
     * f[3] = 3;
     * f[4] = 5;
     * f[5] = 8;
     * f[n] = f[n-1] + f[n-2]
     * */

    public int RectCover(int target) {

        if (target < 4) return target;

        int[] f = new int[target + 1];
        int i;
        for (i=0; i<4; i++) f[i] = i;

        for (i=4; i<=target; i++) {
            f[i] = f[i-1] + f[i-2];
        }

        return f[target];
    }



    public static void main(String[] args) {
        System.out.println(new Rectangle().RectCover(5));
    }
}

【思考】

最直白的结题方式就是找规律，从总结的规律可以看出这是斐波那契数列的实现方式；另一种就是根据题意来解答，求n的方法，这类问题很容易想到是从n-1来求解，而第一个块是横（f[n-2]）是竖(f[n-1])，分别对应不同的情况

（更多相关面试题推荐：java面试题及答案）

3、二进制中 1 的个数

【题目】

输入一个整数，输出该数二进制表示中 1 的个数。其中负数用补码表示。

【代码】

package swear2offer.array;

public class Binary {

    /**
     * 输入一个整数，输出该数二进制表示中 1 的个数。其中负数用补码表示。
     * */
    public int NumberOf1(int n) {
        int count;
        count = 0;

        while(n != 0) {
            n = n & (n-1);// 与操作就是二进制的操作，适用原码和补码
            count ++;
        }

        return count;
    }
}

【思考】

负数的反码： 符号位不变,其余各位按位取反负数的补码：在其反码的基础上+1

如果一个整数不为 0，那么这个整数至少有一位是 1。如果我们把这个整数减 1，那么原来处在整数最右边的 1 就会变为 0，原来在 1 后面的所有的 0 都会变成 1 (如果最右边的 1 后面还有 0 的话)。其余所有位将不会受到影响。

举个例子：一个二进制数 1100，从右边数起第三位是处于最右边的一个 1。减去 1 后，第三位变成 0，它后面的两位 0 变成了 1，而前面的 1 保持不变，因此得到的结果是 1011. 我们发现减 1 的结果是把最右边的一个 1 开始的所有位都取反了。这个时候如果我们再把原来的整数和减去 1 之后的结果做与运算，从原来整数最右边一个 1 那一位开始所有位都会变成 0。如 1100&1011=1000. 也就是说，把一个整数减去 1，再和原整数做与运算，会把该整数最右边一个 1 变成 0. 那么一个整数的二进制有多少个 1，就可以进行多少次这样的操作。

4、数值的整数次方

【题目】

给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent。求 base 的 exponent 次方。
保证 base 和 exponent 不同时为 0

【代码】

package swear2offer.array;

public class Power {

    public double Power(double base, int exponent) {

        if (base == 0) return 0;
        if (exponent == 0) return 1;

        int count;
        boolean flag;
        double temp;

        count = 1;
        temp = base;
        flag = true;// 标记正负

        if (exponent < 0){
            exponent = -exponent;
            flag = false;
        }

        while (count < exponent) {
            base *= temp;
            count ++;
        }

        if (flag) {
            return base;
        } else {
            return 1/base;
        }

    }

    public static void main(String[] args) {
        System.out.println(new Power().Power(2,-3));
    }

}

【思考】

本题难度并不大，算法也不是很复杂，但是边边角角很容易遗漏，

第一点就是exponent的正负，很容易就漏掉负数的情况

其次，base==0和exponent==0的情况是不一样的

最后，base累乘的时候，是不能用本身的，因为base是不断变大的。

5、调整数组顺序使奇数位于偶数前面

【题目】

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

【代码】

package swear2offer.array;

import java.util.Arrays;

public class OddEven {

    /**
     * 输入一个整数数组，实现一个函数来调整该数组中数字的顺序，
     * 使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，
     * 并保证奇数和奇数，偶数和偶数之间的相对位置不变。
     *
     * 时空复杂度较高的算法：
     * 新建一个数组b，用来保存奇数，在重新变量一次，保存偶数
     * 时空复杂度0(n)
     * */
    public void reOrderArray1(int [] array) {
        int n,i,j;
        n = array.length;

        int[] b = new int[n];

        j = 0;// 用来保存数组B的下标
        for (i=0; i<n; i++) {
            if (array[i]%2 != 0) {
                b[j] = array[i];
                j ++;
            }
        }
        for (i=0; i<n; i++) {
            if (array[i]%2 == 0){
                b[j] = array[i];
                j++;
            }
        }

        for (i=0; i<n; i++) {
            array[i] = b[i];
        }
    }

    /**
     * 采用的冒泡交换以及快速排序的思想：
     * 设定两个游标，游标分别用来标记奇数和偶数的下标，然后交换二者
     * 注意交换二者是无法保证顺序的，交换的ij之间还有进行平移。
     * */
    public void reOrderArray(int [] array) {

        int n,i,j,temp,p;

        n = array.length;
        i = 0;
        j = 0;
        while (i<n && j<n) {
            // i标记偶数下标
            while (i<n) {
                if (array[i]%2 ==0){
                    break;
                } else {
                    i++;
                }
            }
            j = i;
            // j标记奇数下标
            while (j<n) {
                if (array[j]%2 !=0){
                    break;
                } else {
                    j++;
                }
            }
            if (i<n && j<n) {
                // 此时ij已经在遇到的第一个偶数和奇数停下，把ij之间的内容平移
                temp = array[j];
                for (p=j; p>i; p--) {
                    array[p] = array[p-1];
                }
                array[i] = temp;
                // 此时把i,j标记到 未交换前的偶数位置的下一个
                i ++;
                j = i;
            }
        }
    }

    public static void main(String[] args) {
        int[] a = {1,4,6,3,2,5,8};
        int[] b = {2,4,6,1,3,5,7};
        new OddEven().reOrderArray(b);
        System.out.println(Arrays.toString(b));
    }
}

【思考】

显然，创建新数组的方式，是一种取巧的方式，题目要求是需要在本数组上进行操作，第二种方式就是采用在本数组上进行操作的，而这种双游标递进的方式跟快速排序的思想很接近。

相关推荐：java入门

Atas ialah kandungan terperinci java面试中常见的数组题目汇总（二）. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!