基于PHP实现的多元线性回归模拟曲线算法php技巧

这篇文章主要介绍了基于PHP实现的多元线性回归模拟曲线算法,结合具体实例形式分析了多元线性回归模拟曲线算法的原理与相关php实现技巧,需要的朋友可以参考下

本文实例讲述了基于PHP实现的多元线性回归模拟曲线算法。分享给大家供大家参考，具体如下：

多元线性回归模型： y = b1x1 + b2x2 + b3x3 +...... +bnxn;

我们根据一组数据： 类似 arr_x = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]]; arr_y = [5, 10, 15]; 我们最后要求出的是一个数组，包含了从b1 到bn；

方法：利用最小二乘法

公式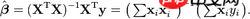：我们只用公式的前半部分，也就是用矩阵来计算

式中的X就是arr_x，二维数组我们可以把它看成是一个矩阵，式中的y就是arr_y，也把它看成一个矩阵(5, 10, 15) ,不过应该是竖着写的。

然后可以根据公式我们会发现要用到矩阵的相乘，转置，求逆；所以下面的代码一一给出：

public function get_complement($data, $i, $j) {
  /* x和y为矩阵data的行数和列数 */
  $x = count($data);
  $y = count($data[0]);
  /* data2为所求剩余矩阵 */
  $data2 =[];
  for ($k = 0; $k < $x -1; $k++) {
    if ($k < $i) {
      for ($kk = 0; $kk < $y -1; $kk++) {
        if ($kk < $j) {
          $data2[$k][$kk] = $data[$k][$kk];
        } else {
          $data2[$k][$kk] = $data[$k][$kk +1];
        }
      }
    } else {
      for ($kk = 0; $kk < $y -1; $kk++) {
        if ($kk < $j) {
          $data2[$k][$kk] = $data[$k +1][$kk];
        } else {
          $data2[$k][$kk] = $data[$k +1][$kk +1];
        }
      }
    }
  }
  return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data) {
  $ans = 0;
  if (count($data[0]) === 2) {
    $ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
  } else {
    for ($i = 0; $i < count($data[0]); $i++) {
      $data_temp = $this->get_complement($data, 0, $i);
      if ($i % 2 === 0) {
        $ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
      } else {
        $ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
      }
    }
  }
  return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data) {
  $m = count($data);
  $n = count($data[0]);
  $data2 =[];
  for ($i = 0; $i < $m; $i++) {
    for ($j = 0; $j < $n; $j++) {
      if (($i + $j) % 2 === 0) {
        $data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
      } else {
        $data2[$i][$j] = - $this->cal_det($this->get_complement($data, $i, $j));
      }
    }
  }
  return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data) {
  $i = count($data);
  $j = count($data[0]);
  $data2 =[];
  for ($k2 = 0; $k2 < $j; $k2++) {
    for ($k1 = 0; $k1 < $i; $k1++) {
      $data2[$k2][$k1] = $data[$k1][$k2];
    }
  }
  /*将矩阵转置便可得到伴随矩阵*/
  return $data2;
}
/*求矩阵的逆，输入参数为原矩阵*/
public function inv($data) {
  $m = count($data);
  $n = count($data[0]);
  $data2 =[];
  $det_val = $this->cal_det($data);
  $data2 = $this->ajoint($data);
  for ($i = 0; $i < $m; $i++) {
    for ($j = 0; $j < $n; $j++) {
      $data2[$i][$j] = $data2[$i][$j] / $det_val;
    }
  }
  return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2) {
  /*$data1 为左乘矩阵*/
  $m1 = count($data1);
  $n1 = count($data1[0]);
  $m2 = count($data2);
  $n2 = count($data2[0]);
  $data_new =[];
  if ($n1 !== $m2) {
    return false;
  } else {
    for ($i = 0; $i <= $m1 -1; $i++) {
      for ($k = 0; $k <= $n2 -1; $k++) {
        $data_new[$i][$k] = 0;
        for ($j = 0; $j <= $n1 -1; $j++) {
          $data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
        }
      }
    }
  }
  return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y) {
  $final =[];
  $arr_x_t = $this->trans($arr_x);
  $result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
  foreach ($result as $key => $val) {
    foreach ($val as $_k => $_v) {
      $final[] = $_v;
    }
  }
  return $final;
}

最后的getParams()方法就是最后求b参数数组的方法，传入一个二维数组arr_x， 和一个一维数组arr_y就可以了。

这一般用于大数据分析，根据大数据来模拟和预测下面的发展和走势。

PS：这里为大家推荐两款相关模拟曲线工具供大家参考：

在线多项式曲线及曲线函数拟合工具：
http://tools.jb51.net/jisuanqi/create_fun

在线绘制多项式/函数曲线图形工具：
http://tools.jb51.net/jisuanqi/fun_draw

您可能感兴趣的文章:

PHP双向链表定义与用法示例php技巧

PHP运用foreach神奇的转换数组(实例讲解)php实例

基于php双引号中访问数组元素报错的解决方法php技巧

Atas ialah kandungan terperinci 基于PHP实现的多元线性回归模拟曲线算法php技巧. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!