Rumah >pembangunan bahagian belakang >tutorial php >php堆排序详解
php堆排序详解
- 小云云asal
- 2018-03-29 11:35:262297semak imbas
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值,即A[PARENT[i]] >= A[i]。在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的要求可知,最大的值一定在堆顶。
堆的定义
一个完全二叉树中,任意父结点总是大于或等于(小于或等于)任何一个子节点,则为大顶堆(小顶堆)。
堆的数组存储方式
完全二叉树适合采用顺序存储的方式,因此一个数组可以看成一个完全二叉树。
节点编号:树根起,自上层到下层,每层从左至右,给所有结点顺序编号,能得到一个反映整个二叉树结构的线性序列。
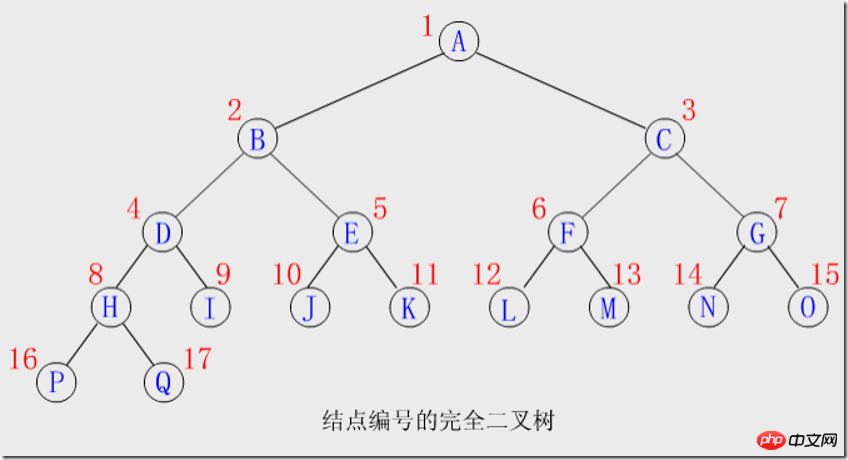
编号特点:
从一个结点的编号就可推得其双亲,左、右孩子,兄弟等结点的编号。假设编号为i的结点是ki(1≤i≤n),则有:
①若i>1,则ki的双亲编号为i/2;若i=1,则Ki是根结点,无双亲。
②若2i≤n,则Ki的左孩子的编号是2i;否则,Ki无左孩子,即Ki必定是叶子。因此完全二叉树中编号i>n/2的结点必定是叶结点。
③若2i+1≤n,则Ki的右孩子的编号是2i+1;否则,Ki无右孩子。
注:ki(0≤i≤n)满足数组下标时,则可能的左右孩子分别为2i+1、2i+2。
堆排序的思想(以大顶堆为例)
利用堆顶记录的是最大关键字这一特性,每一轮取堆顶元素放入有序区,就类似选择排序每一轮选择一个最大值放入有序区,可以把堆排序看成是选择排序的改进。
将初始待排序关键字序列(R0,R1,R2....Rn)构建成大顶堆,此堆为初始的无序区;
将堆顶元素R[0]与最后一个元素R[n]交换,此时得到新的无序区(R0,R1,R2,......Rn-1)和新的有序区(Rn);
由于交换后新的堆顶R[0]可能违反堆的性质,因此需要对当前无序区(R0,R1,R2,......Rn-1)调整为新堆。
不断重复此2、3步骤直到有序区的元素个数为n-1,则整个排序过程完成。
算法分析
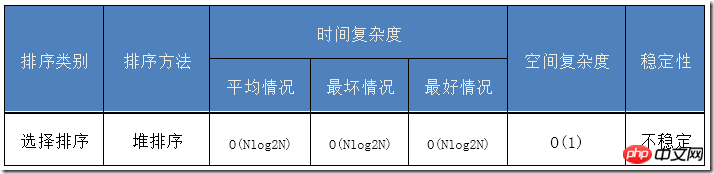
筛选算法
//最难理解的地方
目标:一个所有子树都为堆的完全二叉树。意思就是这个二叉树只差跟节点不满足堆的结构。//很重要,很重要,很重要
如下图:
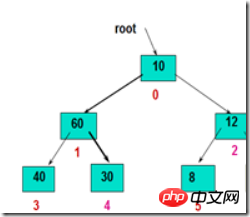
方法:首先将root和它的左右子树的根结点进行比较,把最大的元素交换到root节点;然后顺着被破坏的路径一路调整下去,直至叶子结点,就得到新的堆。
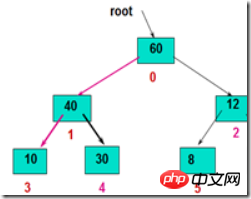
运用:1.在上文提到的堆排序思想,2-3步骤中将无序区调整为堆的时候用到。
2.初始化堆
初始化堆
从最后一个非叶子节点i(i=n/2,n为节点个数)开始,将以i为根节点的二叉树通过筛选调整为堆。以第一张图为例,编号顺序为8、7、6...1。
从最后一个非叶子节就保证了筛选算法的正确性,因为筛选算法的目标是一个所有子树都为堆的完全二叉树。
php实现堆排序:
<?php
//堆排序,对简单排序的改进
function swap(array &$arr,$a,$b)
{
$temp=$arr[$a];
$arr[$a]=$arr[$b];
$arr[$b]=$temp;
}
//调整$arr[$start]的关键字,$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树)
//注意:这里节点s的左右孩子是 2*s +1 和 2*s+2(数组开始下标为0时)
function HeapAdjust(array &$arr $start $end)
{
$temp= $arr[$start];
//沿关键字较大的孩子节点向下筛选
//左右孩子计算 (这里数组的开始下标为0)
//左边孩子 2*$start+1,右边孩子 2*$start+2
for ($j=2*$start+1; $j <=$end; $j=2*$j+1) {
if ($j !=$end &&$arr[$j] <$arr[$j+1]) {
$j++; //转化为右边孩子
}
if ($temp >=$arr[$j]) {
break; //已经满足大根堆
}
//将根节点设置为子节点的较大值
$arr[$start]=$arr[$j];
//继续往下
$start=$j;
}
$arr[$start] =$temp;
}
function HeapSort(array &$arr)
{
$count=count($arr);
//先将数据结构造成大根堆 (由于是完全二叉树,所以这里用floor($count/2-1),下标小于或等于这个数的节点都是有孩子的节点)
for ($i=floor($count /2)-1; $i >=0 ; $i--) {
HeapAdjust($arr,$i,$count);
}
for ($i=$count-1; $i >=0 ; $i--) {
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr,0,$i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新数($arr[0...$i-1])重新调整为大根堆
HeapAdjust($arr,0,$i-1);
}
}
$arr=array(4,1,5,9);
HeapSort($arr);
v相关推荐:
Atas ialah kandungan terperinci php堆排序详解. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Cara menggunakan cURL untuk melaksanakan permintaan Dapatkan dan Hantar dalam PHP
- Cara menggunakan cURL untuk melaksanakan permintaan Dapatkan dan Hantar dalam PHP
- Cara menggunakan cURL untuk melaksanakan permintaan Dapatkan dan Hantar dalam PHP
- Cara menggunakan cURL untuk melaksanakan permintaan Dapatkan dan Hantar dalam PHP
- Semua simbol ungkapan dalam ungkapan biasa (ringkasan)

