Python中基本且又常用的算法

这篇文章主要学习Python常用算法，Python常用排序算法，具有一定的参考价值，感兴趣的小伙伴们可以参考一下

本节内容

算法定义
时间复杂度
空间复杂度
常用算法实例

1.算法定义

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。

一个算法应该具有以下七个重要的特征：

①有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止；

②确切性(Definiteness)：算法的每一步骤必须有确切的定义；

③输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输     入是指算法本身定出了初始条件；

④输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没       有输出的算法是毫无意义的；

⑤可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行       的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）；

⑥高效性(High efficiency)：执行速度快，占用资源少；

⑦健壮性(Robustness)：对数据响应正确。

2. 时间复杂度

计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间,时间复杂度常用大O符号（大O符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；在计算机科学中，它在分析算法复杂性的方面非常有用。）表述，使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。

大O，简而言之可以认为它的含义是“order of”（大约是）。

无穷大渐近

大O符号在分析算法效率的时候非常有用。举个例子，解决一个规模为 n 的问题所花费的时间（或者所需步骤的数目）可以被求得：T(n) = 4n^2 - 2n + 2。
当 n 增大时，n^2; 项将开始占主导地位，而其他各项可以被忽略——举例说明：当 n = 500，4n^2; 项是 2n 项的1000倍大，因此在大多数场合下，省略后者对表达式的值的影响将是可以忽略不计的。

数学表示扫盲贴 python算法表示概念扫盲教程

一、计算方法

1.一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。
一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2.一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f（n），因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，所以f（n）越小，算法的时间复杂度越低，算法的效率越高。
在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

3.常见的时间复杂度

按数量级递增排列，常见的时间复杂度有：
常数阶O(1),  对数阶O(log2n),  线性阶O(n),  线性对数阶O(nlog2n),  平方阶O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k), 指数阶O(2^n) 。
其中，

1.O(n)，O(n^2)， 立方阶O(n^3),...， k次方阶O(n^k) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度。。。。
2.O(2^n)，指数阶时间复杂度，该种不实用
3.对数阶O(log2n),   线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高

例：算法：

 for（i=1;i<=n;++i）
 {
 for(j=1;j<=n;++j)
 {
 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
 for(k=1;k<=n;++k)
 c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
 }
 }

  则有 T（n）= n^2+n^3，根据上面括号里的同数量级，我们可以确定 n^3为T（n）的同数量级
  则有f（n）= n^3，然后根据T（n）/f（n）求极限可得到常数c
  则该算法的 时间复杂度：T（n）=O（n^3)

四、 定义：如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)，它是n的某一函数 T(n)称为这一算法的“时间复杂性”。

当输入量n逐渐加大时，时间复杂性的极限情形称为算法的“渐近时间复杂性”。

我们常用大O表示法表示时间复杂性，注意它是某一个算法的时间复杂性。大O表示只是说有上界，由定义如果f(n)=O(n)，那显然成立f(n)=O(n^2)，它给你一个上界，但并不是上确界，但人们在表示的时候一般都习惯表示前者。

此外，一个问题本身也有它的复杂性，如果某个算法的复杂性到达了这个问题复杂性的下界，那就称这样的算法是最佳算法。

“大O记法”：在这种描述中使用的基本参数是 n，即问题实例的规模，把复杂性或运行时间表达为n的函数。这里的“O”表示量级 (order)，比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”记法 O ( f(n) )表示当 n增大时，运行时间至多将以正比于 f(n)的速度增长。

这种渐进估计对算法的理论分析和大致比较是非常有价值的，但在实践中细节也可能造成差异。例如，一个低附加代价的O(n2)算法在n较小的情况下可能比一个高附加代价的 O(nlogn)算法运行得更快。当然，随着n足够大以后，具有较慢上升函数的算法必然工作得更快。

O(1)

Temp=i;i=j;j=temp;                   

以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=O(1)。如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。

O(n^2)

2.1. 交换i和j的内容

     sum=0；                 （一次）
     for(i=1;i759cb33400b3e1b7405dece1101b3a40左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

例如：求下面树的三种遍历

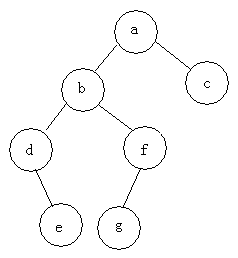
前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

二叉树的类型

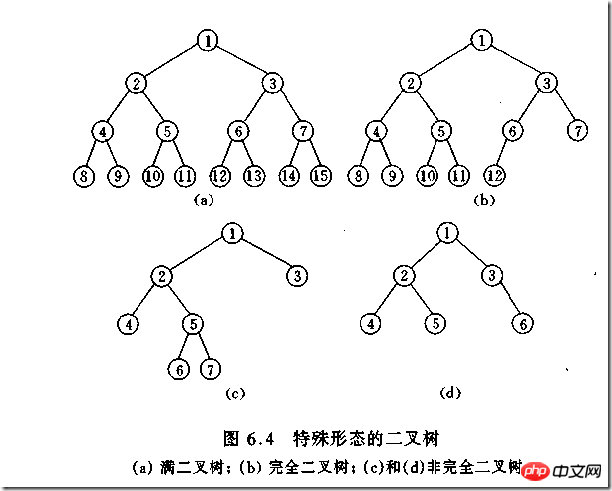
(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

如何判断一棵树是完全二叉树？按照定义

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

如何判断平衡二叉树？

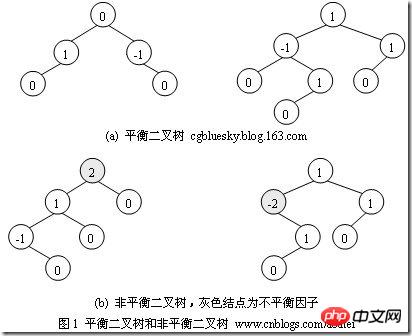
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1

二叉树遍历实现

class TreeNode(object):
 def __init__(self,data=0,left=0,right=0):
 self.data = data
 self.left = left
 self.right = right
 
class BTree(object):
 def __init__(self,root=0):
 self.root = root
 
 
 def preOrder(self,treenode):
 if treenode is 0:
 return
 print(treenode.data)
 self.preOrder(treenode.left)
 self.preOrder(treenode.right)
 def inOrder(self,treenode):
 if treenode is 0:
 return
 self.inOrder(treenode.left)
 print(treenode.data)
 self.inOrder(treenode.right)
 
 def postOrder(self,treenode):
 if treenode is 0:
 return
 self.postOrder(treenode.left)
 self.postOrder(treenode.right)
 print(treenode.data)
if __name__ == '__main__':
 n1 = TreeNode(data=1)
 n2 = TreeNode(2,n1,0)
 n3 = TreeNode(3)
 n4 = TreeNode(4)
 n5 = TreeNode(5,n3,n4)
 n6 = TreeNode(6,n2,n5)
 n7 = TreeNode(7,n6,0)
 n8 = TreeNode(8)
 root = TreeNode('root',n7,n8)
 
 bt = BTree(root)
 print("preOrder".center(50,'-'))
 print(bt.preOrder(bt.root))
 
 print("inOrder".center(50,'-'))
 print (bt.inOrder(bt.root))
 
 print("postOrder".center(50,'-'))
 print (bt.postOrder(bt.root))

堆排序

堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
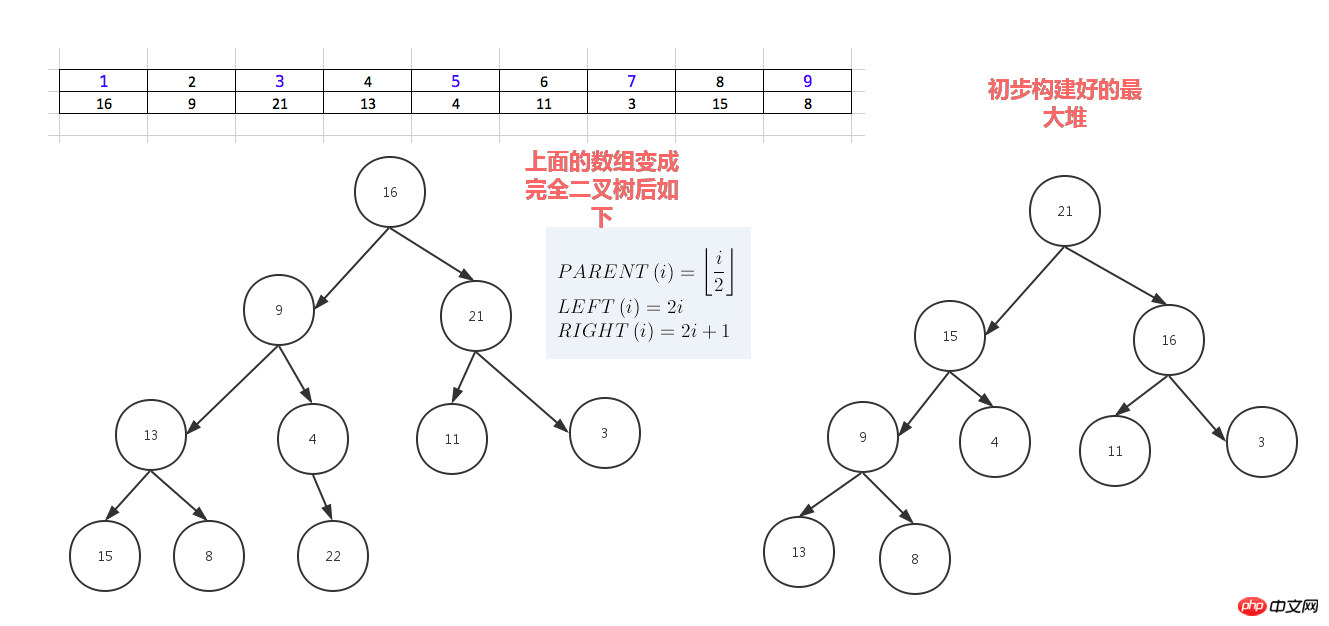
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
 root = node
 #print(root,2*root+1,end)
 while True:
 # 从root开始对最大堆调整
 
 child = 2 * root +1 #left child
 if child > end:
 #print('break',)
 break
 print("v:",root,arr[root],child,arr[child])
 print(arr)
 # 找出两个child中交大的一个
 if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
 child += 1 #设置右边为大
 
 if arr[root] < arr[child]:
 # 最大堆小于较大的child, 交换顺序
 tmp = arr[root]
 arr[root] = arr[child]
 arr[child]= tmp
 
 # 正在调整的节点设置为root
 #print("less1:", arr[root],arr[child],root,child)
 
 root = child #
 #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
 #print("less2:", arr[root],arr[child],root,child)
 else:
 # 无需调整的时候, 退出
 break
 #print(arr)
 print(&#39;-------------&#39;)
 
def heap_sort(arr):
 # 从最后一个有子节点的孩子还是调整最大堆
 first = len(arr) // 2 -1
 for i in range(first, -1, -1):
 sift_down(arr, i, len(arr) - 1)
 #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
 print(&#39;--------end---&#39;,arr)
 # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
 for end in range(len(arr) -1, 0, -1):
 arr[0], arr[end] = arr[end], arr[0]
 sift_down(arr, 0, end - 1)
 #print(arr)
def main():
 # [7, 95, 73, 65, 60, 77, 28, 62, 43]
 # [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
 array = [16,9,21,13,4,11,3,22,8,7,15,29]
 #array = []
 #for i in range(2,5000):
 # #print(i)
 # array.append(random.randrange(1,i))
 
 print(array)
 start_t = time.time()
 heap_sort(array)
 end_t = time.time()
 print("cost:",end_t -start_t)
 print(array)
 #print(l)
 #heap_sort(l)
 #print(l)
 
 
if __name__ == "__main__":
 main()

人类能理解的版本

dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]

for i in range(len(dataset)-1,0,-1):
 print("-------",dataset[0:i+1],len(dataset),i)
 #for index in range(int(len(dataset)/2),0,-1):
 for index in range(int((i+1)/2),0,-1):
 print(index)
 p_index = index

 l_child_index = p_index *2 - 1
 r_child_index = p_index *2
 print("l index",l_child_index,'r index',r_child_index)
 p_node = dataset[p_index-1]
 left_child = dataset[l_child_index]

 if p_node < left_child: # switch p_node with left child
 dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
 #if r_child_index < len(dataset[0:i]): #avoid right out of list index range
 #print(left_child)
 right_child = dataset[r_child_index]
 print(p_index,p_node,left_child,right_child)

 # if p_node < left_child: #switch p_node with left child
 # dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
 # # redefine p_node after the switch ,need call this val below
 # p_node = dataset[p_index - 1]
 #
 if p_node < right_child: #swith p_node with right child
 dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 else:
 print("p node [%s] has no right child" % p_node)


 #最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆

 print("switch i index", i, dataset[0], dataset[i] )
 print("before switch",dataset[0:i+1])
 dataset[0],dataset[i] = dataset[i],dataset[0]
 print(dataset)

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

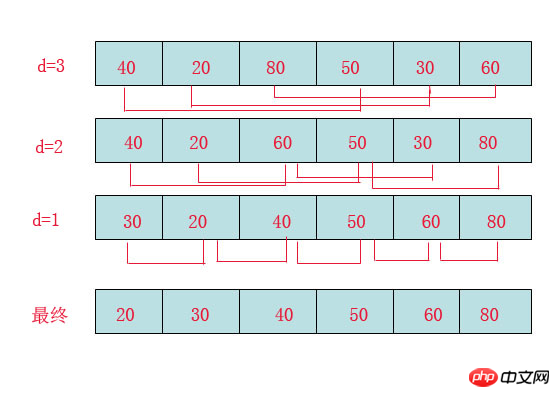
首先要明确一下增量的取法：

第一次增量的取法为： d=count/2;

第二次增量的取法为: d=(count/2)/2;

最后一直到: d=1;

看上图观测的现象为：

d=3时：将40跟50比，因50大，不交换。

              将20跟30比，因30大，不交换。

              将80跟60比，因60小，交换。

d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

              将20跟50比，不交换，继续将50跟80比，不交换。

d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

希尔排序代码

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
 print("---step ---", step)
 #对分组数据进行插入排序

 for index in range(0,len(source)):
 if index + step < len(source):
 current_val = source[index] #先记下来每次大循环走到的第几个元素的值
 if current_val > source[index+step]: #switch
 source[index], source[index+step] = source[index+step], source[index]

 step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
 for index in range(1, len(source)):
 current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
 position = index

 while position > 0 and source[
  position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
 source[position] = source[position - 1] # 把左边的一个元素往右移一位
 position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

 source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
 print(source)

t_end = time.time() - t_start

print("cost:",t_end)

Atas ialah kandungan terperinci Python中基本且又常用的算法. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!