PHP Master | Struktur Data untuk PHP Devs: Grafik

Takeaways Key

• Grafik adalah pembinaan matematik yang digunakan untuk memodelkan hubungan antara pasangan kunci/nilai dan mempunyai banyak aplikasi dunia nyata seperti pengoptimuman rangkaian, penghalaan lalu lintas, dan analisis rangkaian sosial. Mereka terdiri daripada simpang (nod) dan tepi (garisan) yang menghubungkannya, yang boleh diarahkan atau tidak diarahkan, dan berwajaran atau tidak berat.
• Grafik boleh diwakili dalam dua cara: sebagai matriks adjacency atau senarai adjacency. Senarai adjacency lebih cekap ruang, terutamanya untuk graf jarang di mana kebanyakan pasang simpang tidak berkaitan, manakala matriks adjacency memudahkan carian yang lebih cepat.
• Aplikasi biasa teori graf adalah mencari bilangan hop paling sedikit (iaitu, jalan terpendek) antara dua nod. Ini boleh dicapai dengan menggunakan carian terlebih dahulu, yang melibatkan melintasi tahap graf dengan tahap dari nod akar yang ditetapkan. Proses ini memerlukan mengekalkan giliran nod yang tidak disahkan.
Algoritma Dijkstra digunakan secara meluas untuk mencari jalan terpendek atau paling optimum antara dua nod dalam graf. Ini melibatkan memeriksa setiap kelebihan di antara semua pasangan yang mungkin, bermula dari nod sumber, dan mengekalkan set simpul yang dikemas kini dengan jarak keseluruhan terpendek sehingga nod sasaran dicapai.

Dalam salah satu artikel terdahulu saya memperkenalkan anda kepada struktur data pokok. Sekarang saya ingin meneroka struktur yang berkaitan - graf. Grafik mempunyai beberapa aplikasi dunia nyata, seperti pengoptimuman rangkaian, penghalaan lalu lintas, dan analisis rangkaian sosial. PageRank Google, carian graf Facebook, dan cadangan Amazon dan Netflix adalah beberapa contoh aplikasi yang didorong oleh graf. Dalam artikel ini saya akan meneroka dua masalah biasa di mana graf digunakan-bilangan hop dan masalah terpendek. Grafik adalah pembinaan matematik yang digunakan untuk memodelkan hubungan antara pasangan kunci/nilai. Grafik terdiri daripada satu set simpang (nod) dan nombor sewenang -wenang tepi (baris) yang menghubungkannya. Tepi ini boleh diarahkan atau tidak diarahkan. Kelebihan yang diarahkan hanyalah kelebihan antara dua simpul, dan kelebihan A → B tidak dianggap sama dengan B → a. Kelebihan yang tidak diarahkan tidak mempunyai orientasi atau arah; Edge A-B bersamaan dengan B-A. Struktur pokok yang kita pelajari pada masa lalu boleh dianggap sebagai jenis graf yang tidak diarahkan, di mana setiap puncak disambungkan ke sekurang -kurangnya satu puncak lain dengan jalan yang mudah. Graf juga boleh ditimbang atau tidak berat. Graf berwajaran, atau rangkaian, adalah satu di mana berat atau nilai kos diberikan kepada setiap bahagiannya. Graf berwajaran biasanya digunakan dalam menentukan laluan yang paling optimum, paling sesuai, atau laluan "kos" terendah antara dua mata. Arahan memandu Googlemap adalah contoh yang menggunakan graf berwajaran.

bilangan hop paling sedikit

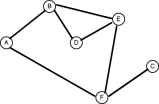
Permohonan teori graf yang biasa adalah mencari bilangan hop paling sedikit di antara dua nod. Seperti pokok, graf boleh dilalui dalam salah satu daripada dua cara: kedalaman pertama atau terlebih dahulu. Kami meliputi carian mendalam pertama dalam artikel sebelumnya, jadi mari kita lihat carian lebar pertama. Pertimbangkan graf berikut:

Demi kesederhanaan, mari kita anggap bahawa graf adalah

tidak diarahkan - iaitu, tepi di mana -mana arah adalah sama. Tugas kami adalah untuk mencari bilangan hop paling sedikit di antara dua nod. Dalam carian terlebih dahulu, kita bermula pada nod akar (atau mana-mana nod yang ditetapkan sebagai akar), dan bekerja di bawah tahap pokok mengikut tahap. Untuk melakukan itu, kita memerlukan giliran untuk mengekalkan senarai nod yang tidak disokong supaya kita dapat mundur dan memprosesnya selepas setiap peringkat. Algoritma Umum kelihatan seperti ini: Tetapi bagaimana kita tahu nod mana yang bersebelahan, apatah lagi tidak disahkan, tanpa melintasi graf pertama? Ini membawa kita kepada masalah bagaimana struktur data graf boleh dimodelkan.

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

mewakili graf

Secara umumnya terdapat dua cara untuk mewakili graf: sama ada sebagai matriks adjacency atau senarai adjacency. Grafik di atas diwakili sebagai senarai adjacency kelihatan seperti ini:

Diwakili sebagai matriks, graf kelihatan seperti ini, di mana 1 menunjukkan "kejadian" kelebihan antara 2 simpang:

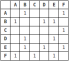
Senarai adjacency adalah lebih cekap ruang, terutamanya untuk graf jarang di mana kebanyakan pasang simpang tidak berkaitan, manakala matriks adjacency memudahkan carian yang lebih cepat. Pada akhirnya, pilihan perwakilan bergantung kepada jenis operasi grafik yang diperlukan. Mari kita gunakan senarai adjacency untuk mewakili graf:

Dan sekarang, mari kita lihat apa pelaksanaan algoritma carian umum terlebih dahulu seperti:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Menjalankan contoh berikut, kami mendapat:

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

Jika kami telah menggunakan timbunan dan bukannya barisan, traversal menjadi carian mendalam-pertama.

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

Mencari laluan terpendek

Satu lagi masalah biasa ialah mencari jalan yang paling optimum antara dua nod. Terdahulu saya menyebut arahan memandu Googlemap sebagai contoh ini. Aplikasi lain termasuk perjalanan perjalanan perjalanan, pengurusan lalu lintas jalan raya, dan penjadualan kereta api/bas. Salah satu algoritma yang paling terkenal untuk menangani masalah ini dicipta pada tahun 1959 oleh seorang saintis komputer berusia 29 tahun dengan nama Edsger W. Dijkstra. Secara umum, penyelesaian Dijkstra melibatkan memeriksa setiap kelebihan di antara semua pasangan yang mungkin bermula dari nod sumber dan mengekalkan satu set simpul yang dikemas kini dengan jarak singkat sehingga nod sasaran dicapai, atau tidak tercapai, mengikut mana -mana yang mungkin berlaku. Terdapat beberapa cara untuk melaksanakan penyelesaian, dan sememangnya, selama bertahun -tahun berikutan 1959 banyak penambahbaikan - menggunakan Minheaps, Priorityqueues, dan Fibonacci Heaps - dibuat untuk algoritma asal Dijkstra. Beberapa prestasi yang lebih baik, sementara yang lain direka untuk menangani kekurangan dalam penyelesaian Dijkstra kerana ia hanya berfungsi dengan graf berwajaran positif (di mana berat adalah nilai positif). Berikut adalah contoh graf berwajaran (positif):

Kita boleh mewakili graf ini sebagai senarai adjacency, seperti berikut:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Dan inilah pelaksanaan menggunakan Priorityqueue untuk mengekalkan senarai semua simpang "tidak dapat dioptimumkan":

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

Seperti yang anda dapat lihat, penyelesaian Dijkstra hanyalah variasi carian terlebih dahulu! Menjalankan contoh berikut menghasilkan hasil berikut:

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

Ringkasan

Dalam artikel ini saya telah memperkenalkan asas -asas teori graf, dua cara mewakili graf, dan dua masalah asas dalam penerapan teori graf. Saya telah menunjukkan kepada anda bagaimana carian terlebih dahulu digunakan untuk mencari bilangan hop paling sedikit di antara mana-mana dua nod, dan bagaimana penyelesaian Dijkstra digunakan untuk mencari jalan terpendek antara dua nod. imej melalui Fotolia

Soalan Lazim (Soalan Lazim) Mengenai Grafik Dalam Struktur Data

Apakah perbezaan antara graf dan pokok dalam struktur data? Pokok adalah sejenis graf, tetapi tidak semua graf adalah pokok. Pokok adalah graf yang disambungkan tanpa sebarang kitaran. Ia mempunyai struktur hierarki dengan nod akar dan nod kanak -kanak. Setiap nod di dalam pokok mempunyai jalan yang unik dari akar. Sebaliknya, graf boleh mempunyai kitaran dan strukturnya lebih kompleks. Ia boleh disambungkan atau terputus dan nod boleh mempunyai pelbagai laluan di antara mereka. senarai. Matriks adjacency adalah saiz 2D saiz V x V di mana v ialah bilangan simpul dalam graf. Sekiranya terdapat kelebihan antara simpang I dan J, maka sel di persimpangan baris I dan Lajur J akan menjadi 1, jika tidak, senarai adjacency adalah pelbagai senarai yang dipautkan. Indeks array mewakili puncak dan setiap elemen dalam senarai yang dipautkannya mewakili simpang lain yang membentuk kelebihan dengan puncak.

Apakah jenis graf dalam struktur data? adalah beberapa jenis graf dalam struktur data. Grafik mudah adalah graf tanpa gelung dan tidak lebih daripada satu kelebihan antara dua titik. Multigraf boleh mempunyai pelbagai tepi antara simpang. Grafik lengkap adalah graf mudah di mana setiap pasangan simpul disambungkan oleh kelebihan. Graf berwajaran memberikan berat kepada setiap kelebihan. Grafik yang diarahkan (atau digraph) mempunyai tepi dengan arah. Titik tepi dari satu puncak ke yang lain.

Apakah aplikasi grafik dalam sains komputer?

Grafik digunakan dalam banyak aplikasi dalam sains komputer. Mereka digunakan dalam rangkaian sosial untuk mewakili hubungan antara orang. Mereka digunakan dalam merangkak web untuk melawat laman web dan membina indeks carian. Mereka digunakan dalam algoritma penghalaan rangkaian untuk mencari jalan terbaik antara dua nod. Mereka digunakan dalam biologi untuk memodelkan dan menganalisis rangkaian biologi. Mereka juga digunakan dalam simulasi grafik komputer dan fizik.

Apakah algoritma traversal graf? (BFS). DFS meneroka sejauh mungkin di sepanjang setiap cawangan sebelum mundur. Ia menggunakan struktur data stack. BFS meneroka semua simpul pada kedalaman sekarang sebelum pergi ke peringkat seterusnya. Ia menggunakan struktur data giliran.

Bagaimana untuk melaksanakan graf di Java? Setiap kunci dalam hashmap adalah puncak dan nilainya adalah senarai yang berkaitan yang mengandungi simpang yang disambungkan ke.

Apakah graf bipartite? dibahagikan kepada dua set disjoint sedemikian rupa sehingga setiap kelebihan menghubungkan puncak dalam satu set ke puncak dalam set yang lain. Tiada kelebihan menghubungkan simpul dalam set yang sama.

Apakah subgraph? Ia mempunyai beberapa (atau semua) simpul grafik asal dan beberapa (atau semua) tepi graf asal.

Apakah kitaran dalam graf? jalan yang bermula dan berakhir di puncak yang sama dan mempunyai sekurang -kurangnya satu kelebihan.

simpang berturut -turut disambungkan oleh kelebihan.

Atas ialah kandungan terperinci PHP Master | Struktur Data untuk PHP Devs: Grafik. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!