1. Definisi
Notasi matematik yang menerangkan had atas masa pelaksanaan atau penggunaan ruang bagi algoritma. Ia dilambangkan sebagai O(f(n)), dengan f(n) ialah fungsi yang mewakili masa atau ruang sebagai fungsi saiz input n .
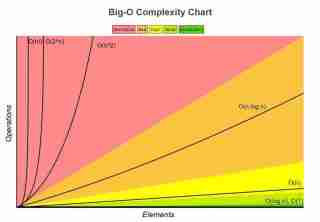
Maklumat lanjut layari: http://bigocheatsheet.com
2. Tujuan
- Perbandingan Algoritma: Membolehkan anda membandingkan algoritma yang berbeza dan memilih yang paling berkesan untuk masalah tertentu.
- Skalabiliti: Membantu meramalkan cara algoritma akan bertindak apabila jumlah data meningkat.
3. Analisis Kerumitan
- Kes Terburuk: Merujuk kepada senario di mana algoritma mengambil masa yang lebih lama atau menggunakan lebih banyak sumber. Big O selalunya merujuk kepada kes ini.
- Kes Terbaik dan Purata Kes: Walaupun penting, ia digunakan kurang kerap untuk tatatanda Big O.
4. Angkasa vs. Masa
- Kerumitan Tempoh: Merujuk kepada masa yang diambil untuk algoritma dilaksanakan.
- Kerumitan Angkasa: Merujuk kepada jumlah memori tambahan yang digunakannya. Ia boleh mempunyai tatatanda seperti O(1) (ruang malar) atau O(n) (ruang linear).
Contoh:
import timeit
import matplotlib.pyplot as plt
import cProfile
# O(1)
def constant_time_operation():
return 42
# O(log n)
def logarithmic_time_operation(n):
count = 0
while n > 1:
n //= 2
count += 1
return count
# O(n)
def linear_time_operation(n):
total = 0
for i in range(n):
total += i
return total
# O(n log n)
def linear_logarithmic_time_operation(n):
if n
<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/173189059010897.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Notación Big O - Python"></p>
<p>Ingat bahawa tidak cukup hanya menggunakan tatatanda besar atau, walaupun ini adalah langkah pertama, terdapat cara lain untuk mengoptimumkan ingatan, contohnya penggunaan <strong>slot</strong>, cache, benang, selari, proses, dsb.</p>
<p>Terima kasih kerana membaca!!<br>
Sokong saya dengan bertindak balas dan memberi pendapat anda.</p>
Atas ialah kandungan terperinci Notasi O Besar - Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Python vs C: Lengkung pembelajaran dan kemudahan penggunaanApr 19, 2025 am 12:20 AM
Python vs C: Lengkung pembelajaran dan kemudahan penggunaanApr 19, 2025 am 12:20 AMPython lebih mudah dipelajari dan digunakan, manakala C lebih kuat tetapi kompleks. 1. Sintaks Python adalah ringkas dan sesuai untuk pemula. Penaipan dinamik dan pengurusan memori automatik menjadikannya mudah digunakan, tetapi boleh menyebabkan kesilapan runtime. 2.C menyediakan kawalan peringkat rendah dan ciri-ciri canggih, sesuai untuk aplikasi berprestasi tinggi, tetapi mempunyai ambang pembelajaran yang tinggi dan memerlukan memori manual dan pengurusan keselamatan jenis.
 Python vs C: Pengurusan dan Kawalan MemoriApr 19, 2025 am 12:17 AM
Python vs C: Pengurusan dan Kawalan MemoriApr 19, 2025 am 12:17 AMPython dan C mempunyai perbezaan yang signifikan dalam pengurusan dan kawalan memori. 1. Python menggunakan pengurusan memori automatik, berdasarkan pengiraan rujukan dan pengumpulan sampah, memudahkan kerja pengaturcara. 2.C memerlukan pengurusan memori manual, memberikan lebih banyak kawalan tetapi meningkatkan risiko kerumitan dan kesilapan. Bahasa mana yang harus dipilih harus berdasarkan keperluan projek dan timbunan teknologi pasukan.
 Python untuk pengkomputeran saintifik: rupa terperinciApr 19, 2025 am 12:15 AM
Python untuk pengkomputeran saintifik: rupa terperinciApr 19, 2025 am 12:15 AMAplikasi Python dalam pengkomputeran saintifik termasuk analisis data, pembelajaran mesin, simulasi berangka dan visualisasi. 1.Numpy menyediakan susunan pelbagai dimensi yang cekap dan fungsi matematik. 2. Scipy memanjangkan fungsi numpy dan menyediakan pengoptimuman dan alat algebra linear. 3. Pandas digunakan untuk pemprosesan dan analisis data. 4.Matplotlib digunakan untuk menghasilkan pelbagai graf dan hasil visual.
 Python dan C: Mencari alat yang betulApr 19, 2025 am 12:04 AM
Python dan C: Mencari alat yang betulApr 19, 2025 am 12:04 AMSama ada untuk memilih Python atau C bergantung kepada keperluan projek: 1) Python sesuai untuk pembangunan pesat, sains data, dan skrip kerana sintaks ringkas dan perpustakaan yang kaya; 2) C sesuai untuk senario yang memerlukan prestasi tinggi dan kawalan asas, seperti pengaturcaraan sistem dan pembangunan permainan, kerana kompilasi dan pengurusan memori manualnya.
 Python untuk sains data dan pembelajaran mesinApr 19, 2025 am 12:02 AM
Python untuk sains data dan pembelajaran mesinApr 19, 2025 am 12:02 AMPython digunakan secara meluas dalam sains data dan pembelajaran mesin, terutamanya bergantung pada kesederhanaannya dan ekosistem perpustakaan yang kuat. 1) PANDAS digunakan untuk pemprosesan dan analisis data, 2) Numpy menyediakan pengiraan berangka yang cekap, dan 3) SCIKIT-Learn digunakan untuk pembinaan dan pengoptimuman model pembelajaran mesin, perpustakaan ini menjadikan Python alat yang ideal untuk sains data dan pembelajaran mesin.
 Pembelajaran Python: Adakah 2 jam kajian harian mencukupi?Apr 18, 2025 am 12:22 AM
Pembelajaran Python: Adakah 2 jam kajian harian mencukupi?Apr 18, 2025 am 12:22 AMAdakah cukup untuk belajar Python selama dua jam sehari? Ia bergantung pada matlamat dan kaedah pembelajaran anda. 1) Membangunkan pelan pembelajaran yang jelas, 2) Pilih sumber dan kaedah pembelajaran yang sesuai, 3) mengamalkan dan mengkaji semula dan menyatukan amalan tangan dan mengkaji semula dan menyatukan, dan anda secara beransur-ansur boleh menguasai pengetahuan asas dan fungsi lanjutan Python dalam tempoh ini.
 Python untuk Pembangunan Web: Aplikasi UtamaApr 18, 2025 am 12:20 AM
Python untuk Pembangunan Web: Aplikasi UtamaApr 18, 2025 am 12:20 AMAplikasi utama Python dalam pembangunan web termasuk penggunaan kerangka Django dan Flask, pembangunan API, analisis data dan visualisasi, pembelajaran mesin dan AI, dan pengoptimuman prestasi. 1. Rangka Kerja Django dan Flask: Django sesuai untuk perkembangan pesat aplikasi kompleks, dan Flask sesuai untuk projek kecil atau sangat disesuaikan. 2. Pembangunan API: Gunakan Flask atau DjangorestFramework untuk membina Restfulapi. 3. Analisis Data dan Visualisasi: Gunakan Python untuk memproses data dan memaparkannya melalui antara muka web. 4. Pembelajaran Mesin dan AI: Python digunakan untuk membina aplikasi web pintar. 5. Pengoptimuman Prestasi: Dioptimumkan melalui pengaturcaraan, caching dan kod tak segerak
 Python vs C: Meneroka Prestasi dan KecekapanApr 18, 2025 am 12:20 AM
Python vs C: Meneroka Prestasi dan KecekapanApr 18, 2025 am 12:20 AMPython lebih baik daripada C dalam kecekapan pembangunan, tetapi C lebih tinggi dalam prestasi pelaksanaan. 1. Sintaks ringkas Python dan perpustakaan yang kaya meningkatkan kecekapan pembangunan. 2. Ciri-ciri jenis kompilasi dan kawalan perkakasan meningkatkan prestasi pelaksanaan. Apabila membuat pilihan, anda perlu menimbang kelajuan pembangunan dan kecekapan pelaksanaan berdasarkan keperluan projek.


Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Dreamweaver Mac版
Alat pembangunan web visual

Muat turun versi mac editor Atom
Editor sumber terbuka yang paling popular

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

MinGW - GNU Minimalis untuk Windows
Projek ini dalam proses untuk dipindahkan ke osdn.net/projects/mingw, anda boleh terus mengikuti kami di sana. MinGW: Port Windows asli bagi GNU Compiler Collection (GCC), perpustakaan import yang boleh diedarkan secara bebas dan fail pengepala untuk membina aplikasi Windows asli termasuk sambungan kepada masa jalan MSVC untuk menyokong fungsi C99. Semua perisian MinGW boleh dijalankan pada platform Windows 64-bit.





