Pokok Rentang Minimum

Pokok rentang minimum graf ialah pokok rentang dengan jumlah pemberat minimum.

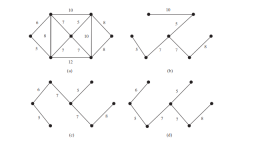
Sebuah graf mungkin mempunyai banyak pokok rentang. Katakan bahawa tepi ditimbang. Pokok rentang minimum mempunyai jumlah berat minimum. Sebagai contoh, pokok-pokok dalam Rajah di bawah b, c, d ialah pokok merentang untuk graf dalam Rajah a. Pokok dalam Rajah c dan d ialah pokok rentang minimum.

Masalah mencari pokok rentang minimum mempunyai banyak aplikasi. Pertimbangkan sebuah syarikat yang mempunyai cawangan di banyak bandar. Syarikat itu ingin memajak talian telefon untuk menghubungkan semua cawangan bersama-sama. Syarikat telefon mengenakan jumlah wang yang berbeza untuk menghubungkan pasangan bandar yang berbeza. Terdapat banyak cara untuk menghubungkan semua cawangan bersama-sama. Cara paling murah ialah mencari pokok spanning dengan jumlah kadar minimum.

Algoritma Pokok Spanning Minimum

Bagaimana anda mencari pokok rentang minimum? Terdapat beberapa algoritma yang terkenal untuk melakukannya. Bahagian ini memperkenalkan algoritma Prim. Algoritma Prim bermula dengan pokok rentang T yang mengandungi bucu arbitrari. Algoritma mengembangkan pokok dengan menambah berulang kali bucu dengan kejadian tepi kos terendah ke bucu yang sudah ada dalam pokok. Algoritma Prim ialah algoritma tamak, dan ia diterangkan dalam kod di bawah.

Input: A connected undirected weighted G = (V, E) with non-negative weights
 Output: MST (a minimum spanning tree)
 1 MST minimumSpanningTree() {
 2 Let T be a set for the vertices in the spanning tree;
 3 Initially, add the starting vertex to T;
 4
 5 while (size of T 



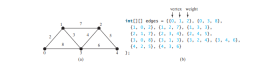
<p>Algoritma bermula dengan menambah titik permulaan ke dalam <strong>T</strong>. Ia kemudian menambah bucu secara berterusan (sebut <strong>v</strong>) daripada <strong>V – T</strong> ke dalam <strong>T</strong>. <strong>v</strong> ialah bucu yang bersebelahan dengan bucu dalam <strong>T</strong> dengan berat terkecil di tepi. Contohnya, terdapat lima tepi yang menyambungkan bucu dalam <strong>T</strong> dan <strong>V – T</strong> seperti yang ditunjukkan dalam Rajah di bawah, dan (<strong>u</strong>, <strong>v</strong> ) ialah yang mempunyai berat paling kecil.</p>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172557408574612.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Minimum Spanning Trees"></p>

<p>Pertimbangkan graf dalam Rajah di bawah. Algoritma menambah bucu kepada <strong>T</strong> dalam susunan ini:</p>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172557408660759.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Minimum Spanning Trees"></p>

<ol>
<li>Tambahkan bucu <strong>0</strong> pada <strong>T</strong>.</li>
<li>Tambah bucu <strong>5</strong> ke <strong>T</strong>, kerana <strong>Tepi(5, 0, 5)</strong> mempunyai berat terkecil antara semua tepi yang bersampingan dengan bucu dalam <strong>T</strong>, seperti yang ditunjukkan dalam Rajah a. Garis anak panah dari <strong>0</strong> hingga <strong>5</strong> menunjukkan bahawa <strong>0</strong> ialah induk kepada <strong>5</strong>.</li>
<li>Tambah bucu <strong>1</strong> ke <strong>T</strong>, kerana <strong>Tepi(1, 0, 6)</strong> mempunyai berat terkecil antara semua tepi yang bersampingan dengan bucu dalam <strong>T</strong>, seperti yang ditunjukkan dalam Rajah b.</li>
<li>Tambah bucu <strong>6</strong> ke <strong>T</strong>, kerana <strong>Tepi(6, 1, 7)</strong> mempunyai berat terkecil antara semua tepi yang bersampingan dengan bucu dalam <strong>T</strong>, seperti yang ditunjukkan dalam Rajah c.</li>
<li>Tambah bucu <strong>2</strong> ke <strong>T</strong>, kerana <strong>Tepi(2, 6, 5)</strong> mempunyai berat terkecil antara semua tepi yang bersampingan dengan bucu dalam <strong>T</strong>, seperti yang ditunjukkan dalam Rajah d.</li>
<li>Tambah bucu <strong>4</strong> ke <strong>T</strong>, kerana <strong>Tepi(4, 6, 7)</strong> mempunyai berat terkecil antara semua tepi yang bersampingan dengan bucu dalam <strong>T</strong>, seperti yang ditunjukkan dalam Rajah e.</li>
<li>Tambah bucu <strong>3</strong> ke <strong>T</strong>, kerana <strong>Tepi(3, 2, 8)</strong> mempunyai berat terkecil antara semua tepi yang bersampingan dengan bucu dalam <strong>T</strong>, seperti yang ditunjukkan dalam Rajah f.</li>
</ol>

<p>Pokok rentang minimum tidak unik. Sebagai contoh, kedua-dua (c) dan (d) dalam Rajah di bawah adalah pokok rentang minimum untuk graf dalam Rajah a. Walau bagaimanapun, jika pemberat berbeza, graf mempunyai pokok rentang minimum yang unik.</p>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172557408958347.jpg?x-oss-process=image/resize,p_40" class="lazy" alt="Minimum Spanning Trees"></p>

<p>Anggap bahawa graf bersambung dan tidak berarah. Jika graf tidak disambungkan atau diarahkan, algoritma tidak akan berfungsi. Anda boleh mengubah suai algoritma untuk mencari hutan merentang untuk sebarang graf tidak terarah. Hutan merentang ialah graf di mana setiap komponen yang disambungkan ialah pokok.</p>

<h2>
  
  
  Refining Prim’s MST Algorithm
</h2>

<p>To make it easy to identify the next vertex to add into the tree, we use <strong>cost[v]</strong> to store the cost of adding a vertex <strong>v</strong> to the spanning tree <strong>T</strong>. Initially <strong>cost[s]</strong> is <strong>0</strong> for a starting vertex and assign infinity to <strong>cost[v]</strong> for all other vertices. The algorithm repeatedly finds a vertex <strong>u</strong> in <strong>V – T</strong> with the smallest <strong>cost[u]</strong> and moves <strong>u</strong> to <strong>T</strong>. The refined version of the alogrithm is given in code below.<br>
</p>

<pre class="brush:php;toolbar:false">Input: A connected undirected weighted G = (V, E) with non-negative weights
Output: a minimum spanning tree with the starting vertex s as the root
 1 MST getMinimumSpanngingTree(s) {
 2 Let T be a set that contains the vertices in the spanning tree;
 3 Initially T is empty;
 4 Set cost[s] = 0; and cost[v] = infinity for all other vertices in V;
 5
 6 while (size of T  w(u, v)) { // Adjust cost[v]
11 cost[v] = w(u, v); parent[v] = u;
12 }
13 }
14 }

Implementation of the MST Algorithm

The getMinimumSpanningTree(int v) method is defined in the WeightedGraph class. It returns an instance of the MST class, as shown in Figure below.

The MST class is defined as an inner class in the WeightedGraph class, which extends the Tree class, as shown in Figure below.

The Tree class was shown in Figure below. The MST class was implemented in lines 141–153 in WeightedGraph.java.

The refined version of the Prim’s algoruthm greatly simplifies the implementation. The getMinimumSpanningTree method was implemented using the refined version of the Prim’s algorithm in lines 99–138 in Listing 29.2. The getMinimumSpanningTree(int startingVertex) method sets cost[startingVertex] to 0 (line 105) and cost[v] to infinity for all other vertices (lines 102–104). The parent of startingVertex is set to -1 (line 108). T is a list that stores the vertices added into the spanning tree (line 111). We use a list for T rather than a set in order to record the order of the vertices added to T.

Initially, T is empty. To expand T, the method performs the following operations:

1. Find the vertex u with the smallest cost[u] (lines 118–123 and add it into T (line 125).
2. After adding u in T, update cost[v] and parent[v] for each v adjacent to u in V-T if cost[v] > w(u, v) (lines 129–134).

After a new vertex is added to T, totalWeight is updated (line 126). Once all vertices are added to T, an instance of MST is created (line 137). Note that the method will not work if the graph is not connected. However, you can modify it to obtain a partial MST.

The MST class extends the Tree class (line 141). To create an instance of MST, pass root, parent, T, and totalWeight (lines 144-145). The data fields root, parent, and searchOrder are defined in the Tree class, which is an inner class defined in AbstractGraph.

Note that testing whether a vertex i is in T by invoking T.contains(i) takes O(n) time, since T is a list. Therefore, the overall time complexity for this implemention is O(n3).

The code below gives a test program that displays minimum spanning trees for the graph in Figure below and the graph in Figure below a, respectively.

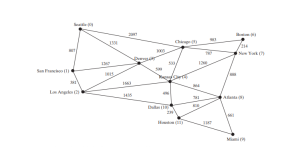
package demo;

public class TestMinimumSpanningTree {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<string> graph1 = new WeightedGraph(vertices, edges);
        WeightedGraph<string>.MST tree1 = graph1.getMinimumSpanningTree();
        System.out.println("Total weight is " + tree1.getTotalWeight());
        tree1.printTree();

        edges = new int[][]{
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };

        WeightedGraph<integer> graph2 = new WeightedGraph(edges, 5);
        WeightedGraph<integer>.MST tree2 = graph2.getMinimumSpanningTree(1);
        System.out.println("\nTotal weight is " + tree2.getTotalWeight());
        tree2.printTree();
    }

}

</integer></integer></string></string>

Total weight is 6513.0
Root is: Seattle
Edges: (Seattle, San Francisco) (San Francisco, Los Angeles)
(Los Angeles, Denver) (Denver, Kansas City) (Kansas City, Chicago)
(New York, Boston) (Chicago, New York) (Dallas, Atlanta)
(Atlanta, Miami) (Kansas City, Dallas) (Dallas, Houston)

Total weight is 14.0
Root is: 1
Edges: (1, 0) (3, 2) (1, 3) (2, 4)

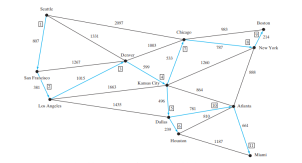
Atur cara mencipta graf berwajaran untuk Rajah di atas dalam baris 27. Ia kemudian memanggil getMinimumSpanningTree() (baris 28) untuk mengembalikan MST yang mewakili pokok rentang minimum untuk graf. Menyebut printTree() (baris 30) pada objek MST memaparkan tepi dalam pokok. Ambil perhatian bahawa MST ialah subkelas Pokok. Kaedah printTree() ditakrifkan dalam kelas Tree.

Ilustrasi grafik bagi pokok rentang minimum ditunjukkan dalam Rajah di bawah. Bucu ditambahkan pada pokok dalam susunan ini: Seattle, San Francisco, Los Angeles, Denver, Kansas City, Dallas, Houston, Chicago, New York, Boston, Atlanta dan Miami.

Atas ialah kandungan terperinci Pokok Rentang Minimum. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!