Mencari Laluan Terpendek

Laluan terpendek antara dua bucu ialah laluan dengan jumlah berat minimum.
Memandangkan graf dengan pemberat bukan negatif di tepi, algoritma terkenal untuk mencari laluan terpendek antara dua bucu ditemui oleh Edsger Dijkstra, seorang saintis komputer Belanda. Untuk mencari laluan terpendek dari bucu s ke bucu v, algoritma Dijkstra mencari laluan terpendek dari s ke semua bucu. Jadi algoritma Dijkstra dikenali sebagai sumber tunggal algoritma laluan terpendek. Algoritma menggunakan kos[v] untuk menyimpan kos laluan terpendek dari bucu v ke bucu sumber s. kos[s] ialah 0. Pada mulanya tetapkan infiniti kepada kos[v] untuk semua bucu lain. Algoritma berulang kali mencari bucu u dalam V – T dengan kos[u] terkecil dan bergerak u ke T .

Algoritma diterangkan dalam kod di bawah.

Input: a graph G = (V, E) with non-negative weights
Output: a shortest path tree with the source vertex s as the root
 1 ShortestPathTree getShortestPath(s) {
 2 Let T be a set that contains the vertices whose
 3 paths to s are known; Initially T is empty;
 4 Set cost[s] = 0; and cost[v] = infinity for all other vertices in V;
 5
 6 while (size of T  cost[u] + w(u, v)) {
11 cost[v] = cost[u] + w(u, v); parent[v] = u;
12 }
13 }
14 }

Algoritma ini sangat serupa dengan Prim untuk mencari pokok rentang minimum. Kedua-dua algoritma membahagikan bucu kepada dua set: T dan V - T. Dalam kes algoritma Prim, set T mengandungi bucu yang telah ditambahkan pada pokok. Dalam kes Dijkstra, set T mengandungi bucu yang laluan terpendeknya ke sumber telah ditemui. Kedua-dua algoritma berulang kali mencari bucu daripada V – T dan menambahnya pada T. Dalam kes algoritma Prim, bucu adalah bersebelahan dengan beberapa bucu dalam set dengan berat minimum di tepi. Dalam algoritma Dijkstra, bucu bersebelahan dengan beberapa bucu dalam set dengan jumlah kos minimum kepada sumber.

Algoritma bermula dengan menetapkan kos[s] kepada 0 (baris 4), menetapkan kos[v] kepada infiniti untuk semua bucu lain. Ia kemudian menambah bucu secara berterusan (katakan u) daripada V – T ke T dengan terkecil kos[u] (baris 7– 8), seperti yang ditunjukkan dalam Rajah di bawah a. Selepas menambah u pada T, algoritma mengemas kini kos[v] dan ibu bapa[v] untuk setiap v bukan dalam T jika (u, v) berada dalam T dan kos[v] > kos[u] + w(u, v) (baris 10–11).

Mari kita menggambarkan algoritma Dijkstra menggunakan graf dalam Rajah di bawah a. Katakan puncak sumber ialah 1. Oleh itu, kos[1] = 0 dan kos untuk semua bucu lain pada mulanya ialah ∞, seperti ditunjukkan dalam Rajah di bawah b. Kami menggunakan ibu bapa[i] untuk menandakan ibu bapa i dalam laluan. Untuk kemudahan, tetapkan induk nod sumber kepada -1.

Pada mulanya ditetapkan T adalah kosong. Algoritma memilih puncak dengan kos terkecil. Dalam kes ini, bucu ialah 1. Algoritma menambah 1 kepada T, seperti yang ditunjukkan dalam Rajah di bawah a. Selepas itu, ia melaraskan kos untuk setiap bucu bersebelahan dengan 1. Kos untuk bucu 2, 0, 6 dan 3 dan ibu bapa mereka kini dikemas kini, seperti yang ditunjukkan, seperti ditunjukkan dalam Rajah di bawah b.

Bucu 2, 0, 6 dan 3 bersebelahan dengan bucu sumber dan bucu 2 ialah yang dalam V-T dengan kos terkecil, jadi tambah 2 kepada T, seperti yang ditunjukkan dalam Rajah di bawah dan kemas kini kos dan induk untuk bucu dalam V-T dan bersebelahan dengan 2. kos[0] kini dikemas kini kepada 6 dan induknya ditetapkan kepada 2. Garis anak panah dari 1 hingga 2 menunjukkan bahawa 1 ialah induk kepada 2 selepas 2 ditambah ke dalam T.

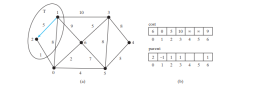
Kini T mengandungi {1, 2}. Puncak 0 ialah satu dalam V-T dengan kos terkecil, jadi tambahkan 0 kepada T, seperti ditunjukkan dalam Rajah di bawah dan kemas kini kos dan induk untuk bucu dalam V-T dan bersebelahan dengan 0 jika berkenaan. kos[5] kini dikemas kini kepada 10 dan induknya ditetapkan kepada 0 dan kos[6] kini dikemas kini kepada 8 dan induknya ditetapkan kepada 0.

Kini T mengandungi {1, 2, 0}. Puncak 6 ialah satu dalam V-T dengan kos terkecil, jadi tambah 6 kepada T, seperti yang ditunjukkan dalam Rajah di bawah dan kemas kini kos dan induk untuk bucu dalam V-T dan bersebelahan dengan 6 jika berkenaan.

Kini T mengandungi {1, 2, 0, 6}. Puncak 3 atau 5 ialah satu dalam V-T dengan kos terkecil. Anda boleh menambah sama ada 3 atau 5 ke dalam T. Mari kita tambahkan 3 kepada T, seperti yang ditunjukkan dalam Rajah di bawah dan kemas kini kos dan induk untuk bucu dalam V-T dan bersebelahan dengan 3 jika berkenaan. kos[4] kini dikemas kini kepada 18 dan induknya ditetapkan kepada 3.

Kini T mengandungi {1, 2, 0, 6, 3}. Puncak 5 ialah satu dalam V-T dengan kos terkecil, jadi tambah 5 kepada T, seperti ditunjukkan dalam Rajah di bawah dan kemas kini kos dan induk untuk bucu dalam V-T dan bersebelahan dengan 5 jika berkenaan. kos[4] kini dikemas kini kepada 10 dan induknya ditetapkan kepada 5.

Kini T mengandungi {1, 2, 0, 6, 3, 5}. Puncak 4 ialah satu dalam V-T dengan kos terkecil, jadi tambahkan 4 kepada T, seperti ditunjukkan dalam Rajah di bawah.

Seperti yang anda boleh lihat, algoritma pada dasarnya mencari semua laluan terpendek dari puncak sumber, yang menghasilkan pokok yang berakar pada puncak sumber. Kami memanggil pokok ini pokok laluan terpendek sumber tunggal (atau ringkasnya pokok laluan terpendek). Untuk memodelkan pokok ini, tentukan kelas bernama ShortestPathTree yang memanjangkan kelas Tree, seperti ditunjukkan dalam Rajah di bawah. ShortestPathTree ditakrifkan sebagai kelas dalaman dalam WeightedGraph dalam baris 200–224 dalam WeightedGraph.java.

Kaedah getShortestPath(int sourceVertex) telah dilaksanakan dalam baris 156–197 dalam WeightedGraph.java. Kaedah menetapkan kos[sourceVertex] kepada 0 (baris 162) dan kos[v] kepada infiniti untuk semua bucu lain (baris 159–161). Induk sourceVertex ditetapkan kepada -1 (baris 166). T ialah senarai yang menyimpan bucu yang ditambahkan ke dalam pepohon laluan terpendek (baris 169). Kami menggunakan senarai untuk T dan bukannya satu set untuk merekodkan susunan bucu yang ditambahkan pada T.

Pada mulanya, T kosong. Untuk mengembangkan T, kaedah melaksanakan operasi berikut:

1. Find the vertex u with the smallest cost[u] (lines 175–181) and add it into T (line 183).
2. After adding u in T, update cost[v] and parent[v] for each v adjacent to u in V-T if cost[v] > cost[u] + w(u, v) (lines 186–192).

Once all vertices from s are added to T, an instance of ShortestPathTree is created (line 196).

The ShortestPathTree class extends the Tree class (line 200). To create an instance of ShortestPathTree, pass sourceVertex, parent, T, and cost (lines 204–205). sourceVertex becomes the root in the tree. The data fields root, parent, and searchOrder are defined in the Tree class, which is an inner class defined in AbstractGraph.

Note that testing whether a vertex i is in T by invoking T.contains(i) takes O(n) time, since T is a list. Therefore, the overall time complexity for this implemention is O(n^3).

Dijkstra’s algorithm is a combination of a greedy algorithm and dynamic programming. It is a greedy algorithm in the sense that it always adds a new vertex that has the shortest distance to the source. It stores the shortest distance of each known vertex to the source and uses it later to avoid redundant computing, so Dijkstra’s algorithm also uses dynamic programming.

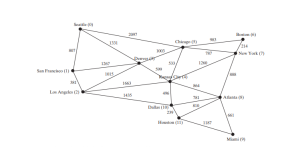
The code below gives a test program that displays the shortest paths from Chicago to all other cities in Figure below and the shortest paths from vertex 3 to all vertices for the graph in Figure below a, respectively.

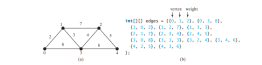
package demo;

public class TestShortestPath {

    public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<string> graph1 = new WeightedGraph(vertices, edges);
        WeightedGraph<string>.ShortestPathTree tree1 = graph1.getShortestPath(graph1.getIndex("Chicago"));
        tree1.printAllPaths();

        // Display shortest paths from Houston to Chicago       
        System.out.println("Shortest path from Houston to Chicago: ");
        java.util.List<string> path = tree1.getPath(graph1.getIndex("Houston"));
        for(String s: path) {
            System.out.print(s + " ");
        }

        edges = new int[][]{
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };

        WeightedGraph<integer> graph2 = new WeightedGraph(edges, 5);
        WeightedGraph<integer>.ShortestPathTree tree2 = graph2.getShortestPath(3);
        System.out.println("\n");
        tree2.printAllPaths();
    }

}

</integer></integer></string></string></string>

All shortest paths from Chicago are:
A path from Chicago to Seattle: Chicago Seattle (cost: 2097.0)
A path from Chicago to San Francisco:
Chicago Denver San Francisco (cost: 2270.0)
A path from Chicago to Los Angeles:
Chicago Denver Los Angeles (cost: 2018.0)
A path from Chicago to Denver: Chicago Denver (cost: 1003.0)
A path from Chicago to Kansas City: Chicago Kansas City (cost: 533.0)
A path from Chicago to Chicago: Chicago (cost: 0.0)
A path from Chicago to Boston: Chicago Boston (cost: 983.0)
A path from Chicago to New York: Chicago New York (cost: 787.0)
A path from Chicago to Atlanta:
Chicago Kansas City Atlanta (cost: 1397.0)
A path from Chicago to Miami:
Chicago Kansas City Atlanta Miami (cost: 2058.0)
A path from Chicago to Dallas: Chicago Kansas City Dallas (cost: 1029.0)
A path from Chicago to Houston:
Chicago Kansas City Dallas Houston (cost: 1268.0)
Shortest path from Houston to Chicago:
Houston Dallas Kansas City Chicago

All shortest paths from 3 are:
A path from 3 to 0: 3 1 0 (cost: 5.0)
A path from 3 to 1: 3 1 (cost: 3.0)
A path from 3 to 2: 3 2 (cost: 4.0)
A path from 3 to 3: 3 (cost: 0.0)
A path from 3 to 4: 3 4 (cost: 6.0)

The program creates a weighted graph for Figure above in line 27. It then invokes the getShortestPath(graph1.getIndex("Chicago")) method to return a Path object that contains all shortest paths from Chicago. Invoking printAllPaths() on the ShortestPathTree object displays all the paths (line 30).

The graphical illustration of all shortest paths from Chicago is shown in Figure below. The shortest paths from Chicago to the cities are found in this order: Kansas City, New York, Boston, Denver, Dallas, Houston, Atlanta, Los Angeles, Miami, Seattle, and San Francisco.

Atas ialah kandungan terperinci Mencari Laluan Terpendek. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!