Pendaraban Matriks dalam Java

Matriks dalam Java disimpan dalam tatasusunan. Terdapat tatasusunan satu dimensi dan tatasusunan dua dimensi yang ada, yang menyimpan nilai dalam bentuk matriks dalam dimensi yang dikenali sebagai tatasusunan. Terdapat hanya nombor yang disimpan dalam satu dimensi dalam tatasusunan satu dimensi, manakala dalam tatasusunan dua dimensi, nombor disimpan dalam bentuk baris dan lajur. Matriks boleh digunakan untuk menambah, menolak dan mendarab nombor dalam bahasa pengaturcaraan Java. Pendaraban matriks adalah salah satu tugas yang paling rumit dalam metodologi pengaturcaraan Java. Kita perlu melakukan pendaraban matriks dalam Java dalam artikel ini dan menunjukkan cara kita boleh mendarab dua matriks dan memberikan output yang munasabah.

Mulakan Kursus Pembangunan Perisian Percuma Anda

Pembangunan web, bahasa pengaturcaraan, ujian perisian & lain-lain

Kaedah Umum

Pendaraban matriks dalam bahasa pengaturcaraan Java dijalankan dengan cara yang sangat mudah. Mula-mula, kami memasukkan nombor dalam tatasusunan dua dimensi pertama dan kemudian kami memasukkan nombor elemen dalam tatasusunan dua dimensi kedua. Nombor-nombor itu ditambah mengikut baris, yang bermaksud bahawa baris pertama dicipta, kemudian nombor dalam baris kedua dicipta dan seterusnya. Kemudian matriks kedua dicipta dengan cara yang sama, dan kemudian kita mula mendarab nombor dalam matriks.

Contoh Pendaraban Matriks dalam Java

Di bawah adalah contoh pendaraban matriks

Contoh #1

Dalam contoh pengekodan, kita melihat bagaimana dua matriks dimasukkan mengikut baris dan kemudian pendaraban matriks dijalankan. Kod untuk pendaraban dua matriks ditunjukkan di bawah. Terdapat tiga tatasusunan yang diisytiharkan. Hasil darab matriks pertama dan kedua ditunjukkan di dalam matriks ketiga. Kemudian matriks ditunjukkan sebagai output yang merupakan hasil darab dua matriks dalam tatasusunan.

Kod:

import java.util.Scanner;
public class MatixMultiplication
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise.  \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
b[i][j] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
System.out.print(c[i][j] + " ");
}
System.out.println();
}
input.close();
}
}

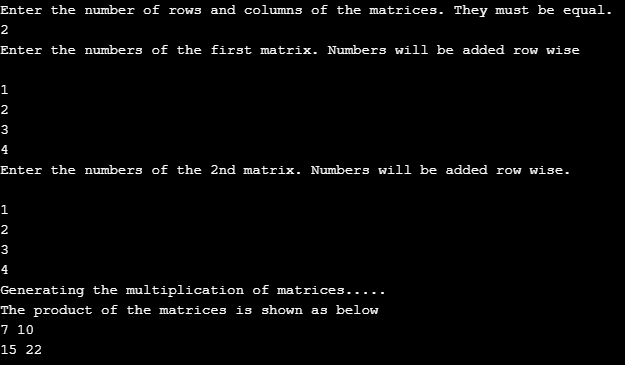
Output untuk matriks 2*2 ditunjukkan. Matriks pertama terdiri daripada elemen sebagai { 1,2

3,4}

dan matriks kedua juga mengandungi elemen yang sama. Dalam output sampel, kita perhatikan pendaraban matriks dan output sampel. Unsur-unsur matriks dihasilkan dengan cara yang sangat bagus. Output yang dihasilkan

{1,2                           { 1,2                                      { 7, 10

3,4}        *                3,4}              =                       15, 22}

Output:

Contoh #2

Dalam pengekodan contoh 2, kami mempunyai atur cara yang sama, tetapi kini kami menggunakan tatasusunan 3 dimensi untuk pendaraban. Kami kini menggunakan pendaraban matriks 3 * 3 dan menunjukkan output dalam tatasusunan 3 dimensi yang lain.

Kod:

import java.util.Scanner;
public class Matix
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise.  \n");
for (int z = 0; z < n; z++)
{
for (int k = 0; k < n; k++)
{
b[z][k] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int k = 0; k < n; k++)
{
for (int l = 0; l < n; l++)
{
System.out.print(c[k][l] + " ");
}
System.out.println();
}
input.close();
}
}

Daripada kod sampel kedua, kami mencetak dua matriks 3 * 3. Matriks pertama ialah {1,1,1

1,1,1

1,1,1}

dan matriks kedua juga sama. Pendaraban matriks dijana dengan cara berikut

{1,1,1                          {1,1,1                                                                                                                                                                                                                                                          1,1,1                *          1,1,1                                   =               3,3,31,1,1}                          1,1,1}                                                 3,3,                                                                                                                                                   

Output:

Kesimpulan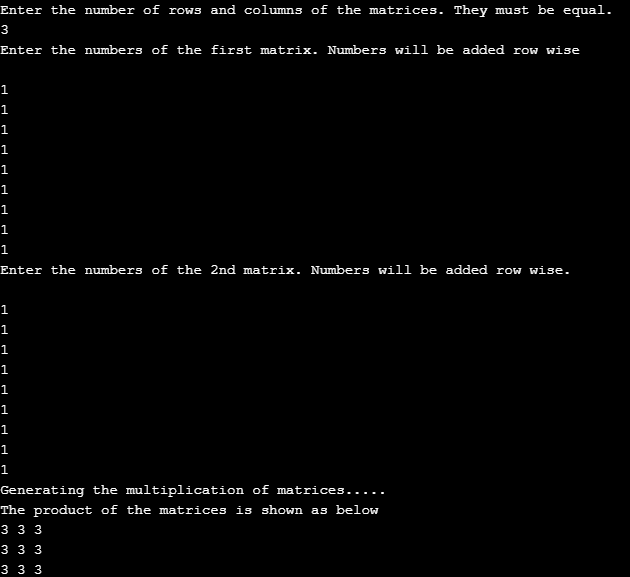

Dalam artikel ini, kita melihat pendaraban matriks 2 * 2 dan matriks 3 * 3 dan output ditunjukkan dengan cara yang sangat bagus. Output diberikan dengan jelas. Menggunakan pendaraban matriks, kita juga boleh mencipta pendaraban 4*4 bagi suatu matriks. Asas ditanya dalam langkah pertama program. Kita boleh mencipta 5 * 5, 6 * 6 matriks juga. Lebih asas lagi adalah kerumitan program.

Walau bagaimanapun, pendaraban mudah matriks sangat berguna dalam mengira pantulan titik dengan paksi-X, paksi-Y atau paksi-Z sebagai paksi pantulan. Konsep mudah ini digunakan dalam geometri koordinat dan digunakan dalam pemodelan matematik aplikasi geometri.

Atas ialah kandungan terperinci Pendaraban Matriks dalam Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!