Rumah >Java >javaTutorial >Rekursi di Jawa
Rekursi di Jawa
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBasal
- 2024-08-30 15:33:33429semak imbas
Rekursi dalam Java ditakrifkan sebagai "kaedah memanggil dirinya sendiri (kaedah yang sama) secara berterusan secara langsung atau tidak langsung." Fungsi rekursi digunakan dalam situasi di mana set operasi yang sama perlu dilakukan berulang kali sehingga keputusan dicapai. Ia melakukan beberapa lelaran, dan penyataan masalah terus menjadi lebih mudah dengan setiap lelaran. Rekursi dalam java ialah kaedah untuk menyelesaikan masalah berdasarkan penyelesaian kepada blok yang lebih kecil daripada masalah yang sama. Kebanyakan lelaran kemungkinan tak terhingga boleh diselesaikan dengan Rekursi. Kita boleh katakan Rekursi ialah cara alternatif untuk menggelungkan kenyataan. Jika kita tidak menggunakan fungsi rekursif dengan betul, ia akan melaksanakan masa yang tidak terhingga.
Sintaks:
IKLAN Kursus Popular dalam kategori ini JAVA MASTERY - Pengkhususan | 78 Siri Kursus | 15 Ujian Olok-olokreturntype methodName()
{
//logic for application
methodName();//recursive call
}
Bagaimanakah Kita Boleh Menghentikan Keadaan Infinite Rekursi di Java?
Untuk menghentikan keadaan tak terhingga, kita mesti mempunyai yang berikut:
- Keadaan Asas: Nyatakan di dalam jika keadaan adalah untuk menghentikan fungsi rekursi.
- Panggilan Rekursi: Panggilan rekursi yang betul.
Kita boleh memanggil fungsi rekursi dalam 2 cara:
1. Panggilan Rekursi Terus
Jika kita panggil kaedah yang sama dari badan kaedah dalam.
Sintaks:
returntype methodName()
{
//logic for application
methodName();//recursive call
}
Contoh:
Faktorial nombor ialah contoh rekursi langsung. Prinsip asas rekursi adalah untuk menyelesaikan masalah yang kompleks dengan membahagikannya kepada yang lebih kecil. Sebagai contoh, dalam kes pemfaktoran nombor, kita mengira pemfaktoran “i” jika kita mengetahui pemfaktorannya bagi “i-1”.
Kod:
public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}
Output:

2. Panggilan Rekursi Tidak Langsung/Saling Bersama
Jika kita memanggil kaedah daripada kaedah lain dan kaedah lain dipanggil daripada kaedah pertama, begitulah sebaliknya.
Sintaks:
<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}
Contoh:
Untuk menunjukkan rekursi tidak langsung, kami mengambil atur cara berikut yang digunakan untuk mengetahui sama ada nombor yang diberikan adalah genap atau ganjil daripada input yang diberikan.
Kod:
import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}
Output:
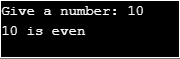
Contoh Rekursi dalam Java
Berikut ialah beberapa lagi contoh untuk menyelesaikan masalah menggunakan kaedah rekursi.
Contoh #1 – Jujukan Fibonacci
Satu set nombor “n” dikatakan berada dalam jujukan Fibonacci jika nombor3=nombor1+nombor2, iaitu setiap nombor ialah hasil tambah dua nombor sebelumnya. Oleh itu urutan sentiasa bermula dengan dua digit pertama seperti 0 dan 1. Digit ketiga ialah hasil tambah 0 dan 1 menghasilkan 1, nombor keempat ialah penambahan 1 dan 1 menghasilkan 2, dan urutan itu berterusan.
Lihat kod berikut dalam Java untuk menjana jujukan Fibonacci:
Kod:
public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}
Output:

Di sini dua nombor pertama dimulakan kepada 0 dan 1 dan dicetak. Pembolehubah "num1", "num2", dan "num3" digunakan untuk menjana urutan yang diperlukan. Pembolehubah "num3" diperoleh dengan menambah "num1" dan "num2", dan nombor dialihkan satu kedudukan ke kiri dengan mengocok seperti yang ditunjukkan dalam kod. Fungsi "Fibonacci" dipanggil secara rekursif di sini, dan pada setiap lelaran, nilai "n" dikurangkan sebanyak 1. Oleh itu rekursi keluar sebaik sahaja "n" mencapai nilai 0.
Contoh #2 – Menara Hanoi
Ini ialah masalah matematik klasik yang mempunyai 3 kutub dan nombor "n" cakera dengan saiz yang berbeza. Teka-tekinya adalah seperti berikut:
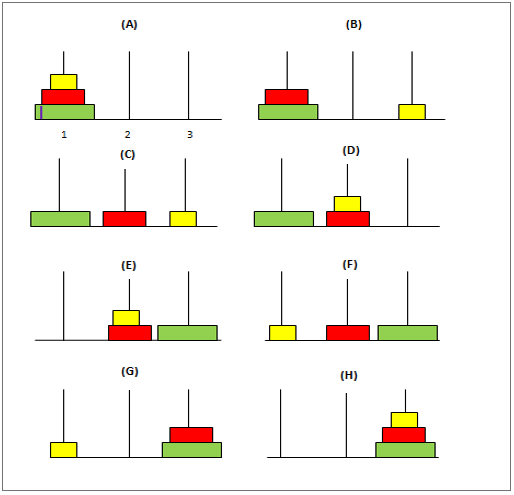
Pada mulanya, tiang pertama akan mempunyai cakera yang disusun supaya cakera terbesar semuanya berada di bahagian bawah dan yang terkecil di bahagian atas tiang. Objektifnya adalah untuk memindahkan cakera ini dari kutub pertama ke kutub ketiga mengekalkan cakera pada kedudukan yang sama seperti pada kutub pertama. Berikut ialah beberapa syarat yang perlu diingat semasa mengalihkan cakera ini:
- Pada satu masa, hanya satu cakera perlu dialihkan.
- Dalam proses itu, meletakkan cakera yang lebih besar di atas cakera yang lebih kecil adalah tidak dibenarkan.
- Kutub kedua (tengah) boleh digunakan untuk pengantara semasa memindahkan cakera dari kutub pertama ke kutub kedua.
Berikut ialah kod Java yang boleh digunakan untuk menyelesaikan teka-teki:
Kod:
public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}
Output:
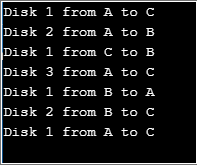
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.
- First, we start by moving disc1 from rod 1 to rod 2.
- Next, we move disc2 to rod 3.
- Finally, we finish by moving disc1 to rod 3, completing the required solution.
This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.
Example #3 – Factorial of Number
Code:
package com.recursion;
import java.util.Scanner;
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}
Output:
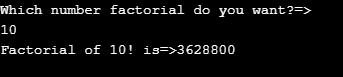
Example #4 – Armstrong Number
Code:
import java.util.Scanner;
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}
Output:
Example #5 – Palindrome Number
Code:
import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}
Output:
Conclusion
Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.
Atas ialah kandungan terperinci Rekursi di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Mengapa hanya satu kelas boleh diisytiharkan sebagai awam dalam fail Java?
- Bagaimanakah Saya Boleh Melaksanakan Perintah Sistem di Java?
- Bagaimana untuk Mengembalikan Ralat \'Bad Request\' HTTP 400 dalam Kaedah Spring MVC @ResponseBody?
- Bagaimana untuk Mendapatkan Nama dan Jenis Parameter Kaedah Menggunakan Refleksi Java?
- Mengapa Pendengar Kunci Saya Tidak Membalas dalam JFrame Saya?

