Program untuk Merge Sort dalam Java

Program untuk Merge Sort dalam Java ialah salah satu algoritma yang paling banyak digunakan dan cekap. Isih gabung adalah berdasarkan teknik bahagi dan takluk yang melibatkan pembahagian masalah yang diberikan kepada berbilang submasalah dan menyelesaikan setiap submasalah secara bebas. Apabila submasalah diselesaikan, kami menggabungkan keputusan mereka untuk mendapatkan penyelesaian akhir kepada masalah tersebut. Algoritma isihan gabungan boleh dilaksanakan menggunakan rekursi kerana ia melibatkan penyelesaian submasalah dan bukannya masalah utama.

Bagaimana Isih Gabungan berfungsi?

Mari kita pertimbangkan tatasusunan yang tidak diisih yang perlu diisih menggunakan algoritma isihan cantum. Berikut ialah langkah-langkah yang terlibat dalam mengisih tatasusunan dengan nilai: 18, 8, 4, 13, 10, 12, 7 dan 11:

Mulakan Kursus Pembangunan Perisian Percuma Anda

Pembangunan web, bahasa pengaturcaraan, ujian perisian & lain-lain

• Langkah pertama melibatkan mencari elemen pangsi atas dasar tatasusunan input kami akan dibahagikan kepada subbarray.
• Mari kita pertimbangkan bahawa elemen 13 dipilih sebagai pangsi; oleh itu, tatasusunan asal akan dibahagikan kepada dua subarray. Subarray pertama akan mengandungi 18, 8, 4, 13 dan subarray kedua akan mengandungi baki elemen 10, 12, 7, 11.
• Subarray yang diperoleh dalam langkah 2 dibahagikan lagi seperti dalam langkah 1, dan ini berterusan.
• Setelah tatasusunan utama dibahagikan kepada subarray dengan elemen tunggal, kami mula menggabungkan subarray ini sekali lagi supaya elemen yang digabungkan berada dalam susunan yang disusun.
• Berikut ialah cara pembahagian dan penaklukan sebenar berfungsi:

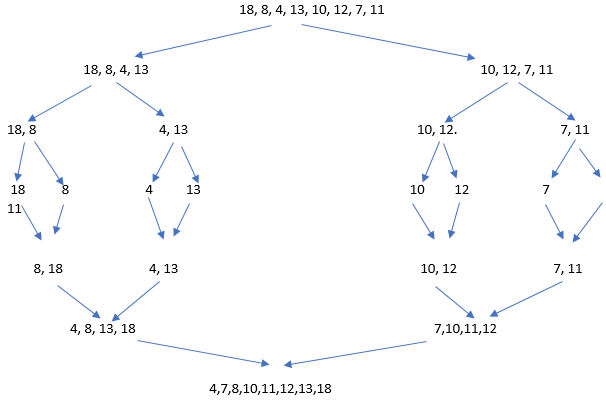
Program untuk Isih Gabungan dalam Java

Berikut ialah contoh kod yang menunjukkan pelaksanaan pengisihan gabungan dalam java:

Kod:

package com.edubca.sorting;
public class MergeSort {
private int[] array;
private int[] tempMergedArr;
private int length;
public static void main(String a[]){
int[] inputArr = {18, 8, 4, 13, 10, 12, 7, 11};
MergeSort mergeSort = new MergeSort();
mergeSort.sort(inputArr);
for(int i:inputArr){
System.out.print(i + " ");
}
}
public void sort(int inputArr[]) {
this.array = inputArr;
this.length = inputArr.length;
this.tempMergedArr = new int[length];
performMergeSort(0, length - 1);
}
private void performMergeSort(int lowerIndex, int higherIndex) {
if (lowerIndex < higherIndex) {
int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
// Sort the left side of the array call performMergeSort recursively
performMergeSort(lowerIndex, middle);
// Sort the right side of the array call performMergeSort recursively
performMergeSort(middle + 1, higherIndex);
// Merge subparts using a temporary array
mergeData(lowerIndex, middle, higherIndex);
}
}
private void mergeData (int lowerIndex, int middle, int higherIndex) {
for (int i = lowerIndex; i <= higherIndex; i++) {
tempMergedArr[i] = array[i];
}
int i = lowerIndex;
int j = middle + 1;
int k = lowerIndex;
while (i <= middle && j <= higherIndex) {
if (tempMergedArr[i] <= tempMergedArr[j]) {
array[k] = tempMergedArr[i];
i++;
} else {
array[k] = tempMergedArr[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = tempMergedArr[i];
k++;
i++;
}
}
}

Kod di atas akan menghasilkan tatasusunan yang diisih sebagai output.

Output:

Bilakah kita harus Menggunakan Isih Gabungan?

Isih gabungan boleh digunakan dalam senario berikut:

• Apabila struktur data yang hendak diisih tidak menyokong akses rawak, maka isihan gabungan boleh membantu dan cekap.
• Apabila tahap selari yang tinggi diperlukan, isihan cantum boleh digunakan kerana submasalah yang berbeza boleh diselesaikan secara bebas menggunakan berbilang proses yang dijalankan secara selari.
• Isih gabungan lebih cepat apabila bekerja dengan senarai terpaut kerana penunjuk boleh ditukar dengan mudah semasa menggabungkan senarai.
• Isih Gabungan boleh dianggap sebagai isihan yang stabil, bermakna elemen yang sama dalam tatasusunan mengekalkan kedudukan asalnya berkenaan antara satu sama lain. Dalam kes di mana kestabilan yang tinggi diperlukan, seseorang boleh menggunakan isihan gabungan. 

Analisis Kerumitan Isih Gabung

Kerumitan analisis di bawah mata bagi jenis cantuman:

• Isih gabung ialah algoritma rekursif dan kerumitan masanya ialah O(n*log n) dalam ketiga-tiga kes (paling teruk, terbaik dan purata) kerana isihan gabungan membahagikan tatasusunan kepada dua bahagian yang sama dan mengambil masa linear untuk menggabungkannya .
• Kerumitan Ruang bagi isihan gabungan ialah O (n) kerana ia beroperasi pada pendekatan rekursif. Oleh itu isihan cantum boleh dianggap sebagai algoritma yang pantas, ruang dan cekap masa.

Membandingkan Isih Gabungan dengan Algoritma Lain

Di bawah mata bandingkan isihan cantuman dengan algoritma lain:

• Isih Timbunan mempunyai kerumitan masa yang sama seperti isihan gabungan, tetapi ia hanya memerlukan ruang tambahan O (1) dan bukannya O (n) isihan gabungan. Oleh itu isihan timbunan adalah lebih cekap ruang daripada isihan gabungan.
• Pelaksanaan Isih Pantas pada umumnya mengatasi prestasi isihan gabungan untuk mengisih tatasusunan berasaskan RAM.
• Isih Gabung mengatasi prestasi algoritma isihan cepat dan timbunan apabila bekerja dengan senarai terpaut kerana penunjuk boleh ditukar dengan mudah.

Kesimpulan-Program untuk Isih Gabungan dalam Java

Artikel tersebut menyimpulkan bahawa isihan gabungan ialah konsep penting untuk difahami apabila ia berkaitan dengan algoritma.

Atas ialah kandungan terperinci Program untuk Merge Sort dalam Java. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!