Laluan dengan Kebarangkalian Maksimum

1514. Laluan dengan Kebarangkalian Maksimum

Kesukaran: Sederhana

Topik: Tatasusunan, Graf, Timbunan (Baris Gilir Keutamaan), Laluan Terpendek

Anda diberi graf berwajaran tidak terarah bagi n nod (0-diindeks), diwakili oleh senarai tepi di mana tepi[i] = [a, b] ialah tepi tidak berarah yang menghubungkan nod a dan b dengan kebarangkalian berjaya merentasi tepi itu succProb[i].

Memandangkan dua nod bermula dan tamat, cari laluan dengan kebarangkalian maksimum kejayaan untuk pergi dari awal hingga akhir dan kembali kebarangkalian kejayaannya.

Jika tiada laluan dari mula hingga akhir, kembali 0. Jawapan anda akan diterima jika ia berbeza daripada jawapan yang betul paling banyak 1e-5.

Contoh 1:

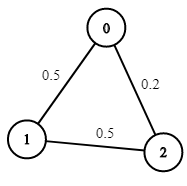
• Input: n = 3, tepi = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], mula = 0, tamat = 2
• Output: 0.25000
• Penjelasan: Terdapat dua laluan dari mula hingga akhir, satu mempunyai kebarangkalian berjaya = 0.2 dan satu lagi mempunyai 0.5 * 0.5 = 0.25.

Contoh 2:

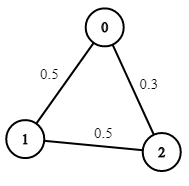
• Input: n = 3, tepi = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], mula = 0, tamat = 2
• Output: 0.30000

Contoh 3:

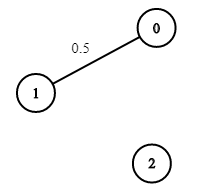
• Input: n = 3, tepi = [[0,1]], succProb = [0.5], mula = 0, tamat = 2
• Output: 0.00000
• Penjelasan: Tiada laluan antara 0 dan 2.

Kekangan:

• 2 <= n <= 10^4
• 0 <= mula, tamat < n
• mula != tamat
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• Terdapat paling banyak satu tepi antara setiap dua nod

Petunjuk:

1. Mendarab kebarangkalian akan mengakibatkan ralat ketepatan.
2. Ambil kebarangkalian log untuk menjumlahkan nombor dan bukannya mendarabnya.
3. Gunakan algoritma Dijkstra untuk mencari laluan minimum antara dua nod selepas menafikan semua kos.

Penyelesaian:

Kami boleh menggunakan versi algoritma Dijkstra yang diubah suai. Daripada mencari jalan terpendek, anda akan memaksimumkan kebarangkalian kejayaan.

Mari laksanakan penyelesaian ini dalam PHP: 1514. Laluan dengan Kebarangkalian Maksimum

<?php
/**
 * @param Integer $n
 * @param Integer[][] $edges
 * @param Float[] $succProb
 * @param Integer $start_node
 * @param Integer $end_node
 * @return Float
 */
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;

echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000


$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;

echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000


$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;

echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>




<h3>
  
  
  Penjelasan:
</h3>

<ol>
<li><p><strong>Perwakilan Graf</strong>: Graf diwakili sebagai senarai bersebelahan di mana setiap nod menghala ke jirannya bersama-sama dengan kebarangkalian kejayaan bagi tepi yang menghubungkannya.</p></li>
<li><p><strong>Max Probability Array</strong>: Tatasusunan maxProb digunakan untuk menyimpan kebarangkalian maksimum untuk mencapai setiap nod dari nod permulaan.</p></li>
<li><p><strong>Baris Gilir Keutamaan</strong>: Timbunan maksimum (SplPriorityQueue) digunakan untuk meneroka laluan dengan kebarangkalian tertinggi dahulu. Ini penting untuk memastikan bahawa apabila kami sampai ke nod destinasi, kami telah menemui laluan dengan kebarangkalian maksimum.</p></li>
<li>
<p><strong>Algoritma</strong>:</p>

<ul>
<li>Mulakan kebarangkalian nod permulaan sebagai 1 (kerana kebarangkalian untuk kekal pada permulaan ialah 1).</li>
<li>Gunakan baris gilir keutamaan untuk meneroka nod, mengemas kini kebarangkalian maksimum untuk mencapai setiap jiran.</li>
<li>Jika nod destinasi tercapai, kembalikan kebarangkalian.</li>
<li>Jika tiada laluan wujud, kembalikan 0.</li>
</ul>
</li>
</ol>

<h3>
  
  
  Output:
</h3>

<p>Untuk contoh yang disediakan:<br>
</p>

<pre class="brush:php;toolbar:false">$n = 3;
$edges = [[0,1],[1,2],[0,2]];
$succProb = [0.5,0.5,0.2];
$start_node = 0;
$end_node = 2;

Keluaran ialah 0.25.

Pendekatan ini memastikan penyelesaian yang cekap menggunakan algoritma Dijkstra semasa mengendalikan spesifik pengiraan kebarangkalian.

Pautan Kenalan

Jika anda mendapati siri ini membantu, sila pertimbangkan untuk memberi repositori bintang di GitHub atau berkongsi siaran pada rangkaian sosial kegemaran anda ?. Sokongan anda amat bermakna bagi saya!

Jika anda mahukan kandungan yang lebih berguna seperti ini, sila ikuti saya:

• LinkedIn
• GitHub

Atas ialah kandungan terperinci Laluan dengan Kebarangkalian Maksimum. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!