Kemajuan dibuat buat pertama kali dalam beberapa dekad, perantis Tao Zhexuan dan Zhao Yufei memecahkan masalah matematik gabungan

Baru-baru ini, buat pertama kalinya, kemajuan telah dicapai pada masalah matematik yang tidak dapat diselesaikan selama beberapa dekad.

Mendorong kemajuan ini ialah pelajar siswazah UCLA James Leng dan pelajar siswazah matematik MIT Ashwin Sah, dan penolong profesor Universiti Columbia Mehtaab Sawhney. Antaranya, James Leng belajar di bawah ahli matematik terkenal Terence Tao, dan Ashwin Sah belajar di bawah master matematik diskret Zhao Yufei.

Alamat kertas: https://arxiv.org/pdf/2402.17995

Untuk memahami kejayaan yang dicapai dalam penyelidikan ini, anda perlu bermula dengan janjang aritmetik.

Jumlah n sebutan pertama bagi jujukan aritmetik dipanggil siri aritmetik, juga dipanggil siri aritmetik. Pada tahun 1936, ahli matematik Paul Erdős dan Pál Turán menjangkakan bahawa jika set terdiri daripada pecahan bukan sifar integer (walaupun 0.00000001%), maka ia mesti mengandungi siri aritmetik yang panjang sewenang-wenangnya. Satu-satunya set yang boleh mengelakkan siri aritmetik ialah set yang mengandungi bahagian integer yang "boleh diabaikan". Contohnya, set {2, 4, 8, 16, …}, di mana setiap nombor ialah dua kali nombor sebelumnya, dihamparkan di sepanjang paksi nombor tanpa janjang.

Pada tahun 1975, ahli matematik Endre Szemerédi membuktikan sangkaan ini. Kerjanya menimbulkan pelbagai arah penyelidikan yang masih diterokai oleh ahli matematik hari ini.

Ahli matematik menetapkan keputusan Szemerédi dalam kes set nombor terhingga (semua integer dari 1 hingga beberapa nombor N). Berapa banyak kumpulan awal boleh digunakan dalam set sebelum tidak dapat tidak termasuk siri terlarang? Bagaimanakah perkadaran ini berubah apabila N berubah?

Sebagai contoh, biarkan N ialah 20, berapa banyakkah daripada 20 nombor ini yang boleh ditulis sambil masih mengelak siri yang panjangnya 5 atau lebih nombor? Jawapannya, ternyata, adalah 16% hingga 80% daripada kumpulan awal.

Szemerédi adalah orang pertama yang menunjukkan bahawa apabila N berkembang, pecahan ini mesti mengecut kepada sifar, dan ahli matematik telah mencuba untuk mengukur seberapa cepat perkara ini berlaku.

Tahun lepas, kerja pecah tanah oleh dua saintis komputer hampir menyelesaikan masalah siri tiga penggal, seperti {6, 11, 16}. Tetapi masalahnya menjadi lebih sukar apabila anda cuba mengelakkan siri aritmetik empat atau lebih istilah. Ini kerana siri yang lebih panjang mencerminkan struktur asas yang sukar didedahkan menggunakan kaedah matematik klasik.

Nombor x, y dan z dalam siri aritmetik tiga sebutan sentiasa memenuhi persamaan mudah x – 2y + z = 0 (mengambil siri {10, 20, 30} sebagai contoh: 10 – 2*(20) + 30 = 0), agak mudah untuk membuktikan sama ada set mengandungi nombor yang memenuhi syarat ini. Walaupun nombor dalam siri empat jangka juga mesti memenuhi persamaan yang lebih kompleks x^2 – 3y^2 + 3z^2 – w^2 = 0, siri dengan lima atau lebih sebutan mesti memenuhi persamaan yang lebih kompleks. Ini bermakna set yang mengandungi siri sedemikian akan mempamerkan corak yang lebih halus. Ia juga akan menjadi lebih sukar bagi ahli matematik untuk membuktikan sama ada corak sedemikian wujud.

Pada penghujung 1990-an, ahli matematik Timothy Gowers mencadangkan satu teori untuk mengatasi halangan ini. Beliau kemudiannya dianugerahkan Fields Medal, penghormatan tertinggi matematik, sebahagiannya untuk kerja ini. Pada tahun 2001, beliau menggunakan kaedahnya pada teorem Szemerédi dan membuktikan terikat yang lebih baik pada saiz set maksimum, mengelakkan siri aritmetik untuk sebarang panjang tertentu.

Pada 2022, James Leng, ketika itu pelajar siswazah tahun kedua di UCLA, mula memahami teori Gowers. Dia tidak menganggap teorem Szemerédi. Sebaliknya, dia berharap dapat menjawab soalan mengenai pendekatan Gowers.

Namun, setelah berusaha bersungguh-sungguh untuk meneroka selama lebih setahun, dia tidak menemui apa-apa.

Sah dan Sawhney, yang telah memikirkan tentang isu berkaitan, mengetahui tentang kerja Leng dan sangat berminat malah Sawhney berkata: "Saya terkejut saya boleh berfikir seperti ini."

Sah dan Sawhney menyedari bahawa penyelidikan Leng mungkin membantu mereka membuat kemajuan selanjutnya dalam teorem Szemerédi. Dalam beberapa bulan, tiga ahli matematik muda memikirkan cara untuk mendapatkan had atas yang lebih baik pada saiz set tanpa siri pentterm. Mereka kemudian memanjangkan kerja mereka kepada siri panjang sewenang-wenangnya, menandakan kemajuan pertama pada masalah itu dalam tempoh 23 tahun sejak bukti Gowers.

Biar 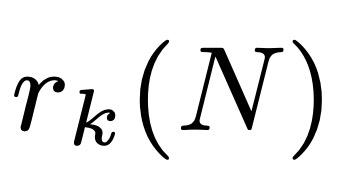menandakan 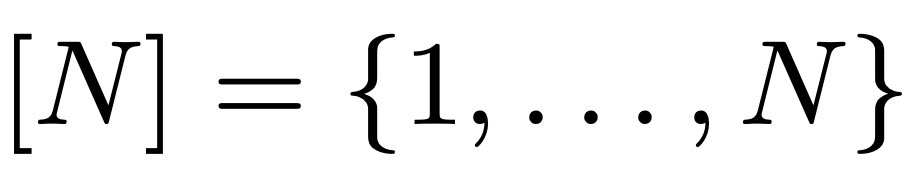, saiz subset terbesar siri aritmetik tanpa sebutan k. Leng, Sah dan Sawhney menunjukkan bahawa untuk k ≥ 5, wujud c_k > 0 sedemikian rupa sehingga .

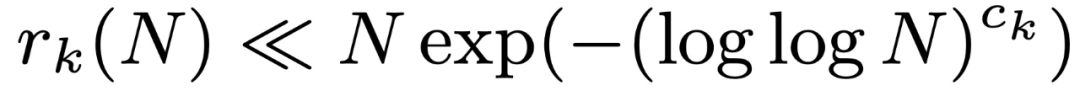Pasukan Penyelidik

Pengarang pertama karya James Leng ialah pelajar siswazah dalam matematik di University of California, Los Angeles (UCLA) dan menerima ijazah sarjana mudanya dari University of California, Berkeley. Dia belajar di bawah ahli matematik terkenal Terence Tao.

Minat penyelidikan James Leng termasuk kombinatorik aritmetik, sistem dinamik, analisis Fourier, dsb. Penyelidikan beliau juga telah disokong oleh persekutuan siswazah NSF.

                                                                                                                                 ^{Pada musim panas 2016, Sah yang berusia 16 tahun memenangi pingat emas dalam International Mathematics Olympiad (IMO) Pada tahun berikutnya dia memasuki MIT untuk belajar. .} Semasa pengajiannya di MIT, terdapat dua orang yang memainkan peranan penting dalam perkembangan matematik Sah. Yang pertama ialah Profesor Yufei Zhao, seorang sarjana matematik diskret, yang juga tutor siswazah Sah.

Yang kedua ialah Mehtaab Sawhney, mereka bertemu dalam kelas dan menjadi kawan. Kemudian, kedua-duanya melakukan penyelidikan bersama dan membincangkan pelbagai topik dalam bidang matematik diskret, seperti teori graf, teori kebarangkalian dan sifat-sifat matriks rawak. Ashwin Sah dan Mehtaab Sawhney bertemu pada penghujung tahun 2017 ketika mereka pelajar sarjana muda di (MIT). Sejak itu, kedua-duanya telah menulis 57 bukti matematik yang luar biasa bersama-sama, kebanyakannya mempunyai akibat yang mendalam dalam pelbagai bidang.

                                                                                                                                     … Minat penyelidikannya termasuk kombinatorik, kebarangkalian, dan sains komputer teori, antara lain.

Pautan rujukan: https://www.quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/

Atas ialah kandungan terperinci Kemajuan dibuat buat pertama kali dalam beberapa dekad, perantis Tao Zhexuan dan Zhao Yufei memecahkan masalah matematik gabungan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!