Rumah >Peranti teknologi >AI >Persoalan utama kebolehjelasan ialah, apakah penjelasan pertama? 20 kertas CCF-A+ICLR memberi anda jawapan
Persoalan utama kebolehjelasan ialah, apakah penjelasan pertama? 20 kertas CCF-A+ICLR memberi anda jawapan
- 王林asal
- 2024-08-05 15:55:55965semak imbas

Lajur AIxiv ialah lajur di mana tapak ini menerbitkan kandungan akademik dan teknikal. Dalam beberapa tahun kebelakangan ini, lajur AIxiv laman web ini telah menerima lebih daripada 2,000 laporan, meliputi makmal terkemuka dari universiti dan syarikat utama di seluruh dunia, mempromosikan pertukaran dan penyebaran akademik secara berkesan. Jika anda mempunyai kerja yang sangat baik yang ingin anda kongsikan, sila berasa bebas untuk menyumbang atau hubungi kami untuk melaporkan. E-mel penyerahan: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
Lihat 1: https://zhuanlan.zhihu.com/p/369883667
Pembelajaran yang mendalam - Disebabkan kekurangan sokongan teori asas, kebanyakan algoritma pembelajaran mendalam semasa adalah empirikal dan kejuruteraan. Prinsip pertama dalam bidang kebolehjelasan seharusnya dapat melaksanakan tugas meringkaskan sejumlah besar pengalaman kejuruteraan generasi terdahulu ke dalam undang-undang saintifik. Di bawah sistem teori kebolehtafsiran interaksi yang setara, pasukan kami telah membuktikan bahawa sifat pengiraan 14 algoritma atribusi kepentingan input yang berbeza boleh disatukan secara matematik dalam bentuk pengagihan semula interaksi. Di samping itu, kami juga menyatukan 12 algoritma untuk meningkatkan kebolehpindahan musuh dan membuktikan bahawa mekanisme biasa semua algoritma untuk meningkatkan kebolehpindahan musuh adalah untuk mengurangkan kesan interaksi antara gangguan musuh, mencapai kebanyakan keupayaan kejuruteraan ke arah kebolehtafsiran rangkaian saraf pemeluwapan algoritma.
Lihat 1: https://zhuanlan.zhihu.com/p/610774894 Lihat 2: https://zhuanlan.zhihu.com/p/5466433 Di bawah sistem teori kebolehtafsiran interaktif yang setara, pasukan kami telah berjaya menerbitkan 20 kertas kerja ICLR persidangan teratas CCF-A dan pembelajaran mesin dalam penyelidikan terdahulu Kami telah menjawab sepenuhnya soalan di atas secara teori dan eksperimen.
Sepanjang rangka kerja teori di atas, dalam artikel Zhihu ini, kami berharap dapat menerangkan dengan tepat peraturan perubahan generalisasi semasa proses latihan rangkaian saraf Dua kertas terlibat. . 2.Qihan Ren, Yang Xu, Junpeng Zhang, Yue Xin, Dongrui Liu, Quanshi Zhang, "Ke Arah Dinamik Interaksi Simbolik Pembelajaran DNN" dalam arXiv:2407.19198 Rajah 1: Gambarajah skematik fenomena dua peringkat. Pada peringkat pertama, rangkaian saraf secara beransur-ansur menghapuskan interaksi peringkat pertengahan dan tinggi dan mempelajari interaksi peringkat rendah pada peringkat kedua, rangkaian saraf secara beransur-ansur memodelkan interaksi tertib yang semakin meningkat; Apabila jurang kerugian antara kehilangan ujian dan kehilangan latihan mula meningkat semasa proses latihan rangkaian saraf, rangkaian saraf akan memasuki peringkat kedua latihan. Kami berharap dapat mencadangkan teori baharu dalam rangka kerja interaksi yang setara untuk meramalkan dengan tepat bilangan, kerumitan dan perubahan generalisasi konsep interaksi yang dipelajari oleh rangkaian saraf pada setiap titik masa (ditunjukkan dalam Rajah 1). Secara khusus, kami berharap dapat membuktikan dua kesimpulan. Iaitu, teori perlu meramalkan dengan tepat perubahan dalam pengagihan konsep interaksi yang dimodelkan oleh rangkaian saraf pada peringkat latihan yang berbeza - untuk menyimpulkan interaksi mana yang akan digunakan pada masa mana Learned . secara objektif mencerminkan perubahan peraturan generalisasi rangkaian saraf sepanjang kitaran latihan. Hubungan dengan pendahulu: Sudah tentu, semua orang mungkin terlebih dahulu memikirkan inti tangen saraf (NTK) [2], tetapi isirong tangen neural hanya menyelesaikan lengkung perubahan parameter, dan tidak boleh pergi lebih jauh tahap logik membuat keputusan tidak mewujudkan hubungan antara perwakilan konsep pemodelan rangkaian saraf dan generalisasinya Analisis generalisasi masih kekal pada tahap analisis ruang ciri, dan tidak ada hubungan antara [logik konsep yang dilambangkan] dan [. logik konsep yang dilambangkan]. Hubungan yang ketat diwujudkan antara kebolehgeneralisasian]. 3. Dua latar belakang penyelidikan utama Salah Faham 1: Perwakilan utama rangkaian saraf ialah "interaksi setara", bukan parameter dan struktur rangkaian saraf Menganalisis rangkaian saraf semata-mata dari peringkat struktur adalah salah faham tentang perwakilan asas generalisasi rangkaian saraf. Pada masa ini, kebanyakan penyelidikan generalisasi rangkaian neural tertumpu terutamanya pada struktur, ciri dan data rangkaian saraf. Adalah dipercayai bahawa struktur rangkaian saraf yang berbeza secara semula jadi sepadan dengan fungsi yang berbeza dan secara semula jadi mempamerkan prestasi yang berbeza. Namun, sebenarnya, seperti yang ditunjukkan dalam Rajah 2, perbezaan dalam struktur hanyalah satu bentuk perwakilan rangkaian saraf yang cetek. Kecuali untuk rangkaian saraf dengan kelemahan yang jelas yang mempunyai kesan ketara terhadap prestasi, semua rangkaian saraf lain dengan struktur berbeza yang boleh mencapai prestasi SOTA sering memodelkan perwakilan interaksi setara yang serupa, iaitu, rangkaian saraf berprestasi tinggi dengan struktur berbeza adalah bersamaan dengan perwakilan Interaktif selalunya membawa kepada matlamat yang sama melalui pendekatan yang berbeza [3, 4]. Walaupun ciri dalaman rangkaian saraf adalah kompleks dan huru-hara, walaupun vektor ciri yang dimodelkan oleh rangkaian saraf yang berbeza sangat berbeza, dan walaupun neuron individu dalam rangkaian saraf sering memodelkan semantik yang agak mengelirukan (semantik tidak jelas), Bagi saraf saraf. rangkaian secara keseluruhan, secara teorinya kami membuktikan bahawa hubungan interaksi yang dimodelkan oleh rangkaian saraf adalah jarang dan simbolik (bukannya ciri-ciri yang jarang, lihat bab "4. Definisi Interaksi" untuk butiran), dan berorientasikan tugas yang sama . Rangkaian saraf yang berbeza sering memodelkan interaksi yang serupa. Rajah 2: Interaksi setara yang dimodelkan oleh rangkaian saraf struktur berbeza selalunya membawa kepada matlamat yang sama. Untuk ayat input yang sama, dua rangkaian saraf yang sama sekali berbeza yang menyasarkan tugas yang sama sering memodelkan interaksi yang serupa. Disebabkan oleh parameter dan sampel latihan yang berbeza bagi rangkaian saraf yang berbeza, tiada neuron dalam kedua-dua rangkaian saraf yang mempunyai perhubungan satu sama satu yang ketat dalam perwakilan, dan setiap neuron sering memodelkan corak pengadunan Semantik yang berbeza. Sebaliknya, seperti yang dianalisis dalam perenggan sebelumnya, perwakilan interaktif yang dimodelkan oleh rangkaian saraf sebenarnya adalah invarian dalam perwakilan rangkaian saraf yang berbeza. Oleh itu, kami mempunyai sebab untuk mempercayai bahawa perwakilan asas rangkaian saraf adalah interaksi yang setara, dan bukannya pembawanya (parameter dan sampel latihan simbolik mungkin mewakili prinsip pertama perwakilan pengetahuan (teorem sparsity berinteraksi, simulator tak terhingga Teorem konsistensi). dan fenomena mencapai destinasi yang sama melalui laluan yang berbeza disediakan dalam bab "4. Definisi Interaksi". Untuk penyelidikan terperinci, lihat artikel Zhihu di bawah Lihat: https://zhuanlan.zhihu.com. /p/633531725 Salah Faham 2: Masalah generalisasi rangkaian saraf ialah masalah model campuran, bukan vektor dalam ruang berdimensi tinggi Seperti yang ditunjukkan dalam Rajah 3, analisis generalisasi tradisional sentiasa menganggap bahawa satu sampel ialah keseluruhan. Titik dalam ruang berdimensi tinggi Sebenarnya, perwakilan sampel tunggal oleh rangkaian saraf adalah dalam bentuk model campuran - sebenarnya dinyatakan melalui sejumlah besar interaksi yang berbeza kebolehan generalisasi interaksi mudah adalah lebih kuat daripada interaksi kompleks, jadi ia tidak lagi sesuai untuk menggunakan skalar mudah untuk secara amnya mewakili keupayaan keseluruhan rangkaian saraf pada sampel yang berbeza, model rangkaian saraf yang sama hubungan interaksi kerumitan yang berbeza pada sampel yang berbeza sering sepadan dengan kebolehan generalisasi yang berbeza Biasanya, interaksi peringkat tinggi (kompleks) yang dimodelkan oleh rangkaian saraf selalunya sukar untuk digeneralisasikan untuk menguji sampel (interaksi yang sama tidak akan dicetuskan pada sampel ujian). , yang mewakili representasi overfitting , dan interaksi tertib rendah (mudah) yang dimodelkan oleh rangkaian saraf sering mewakili representasi dengan generalisasi yang kuat, sila lihat [1] untuk penyelidikan terperinci. Rajah 3: (a) Analisis generalisasi tradisional sentiasa mengandaikan bahawa satu sampel secara keseluruhan adalah titik dalam ruang berdimensi tinggi. (b) Malah, rangkaian saraf mewakili satu sampel dalam bentuk model campuran Rangkaian saraf memodelkan interaksi mudah (interaksi boleh umum) dan interaksi kompleks (interaksi tidak boleh digeneralisasikan) pada satu sampel. 4. Definisi interaksi . Biarkan . Untuk rangkaian saraf yang berorientasikan kepada tugas klasifikasi, kita boleh menentukan keluaran skalarnya daripada perspektif yang berbeza. Contohnya, untuk masalah klasifikasi berbilang kategori,
mewakili output skalar DNN pada sampelboleh ditakrifkan sebagai , atau sebagai output skalar yang sepadan dengan label sebenar sampel sebelum lapisan softmax. Di sini, mewakili kebarangkalian pengelasan bagi label sebenar. Dengan cara ini, untuk setiap subset , kita boleh menggunakan formula berikut untuk mentakrifkan "kesetaraan dan interaksi" dan "kesetaraan atau interaksi" antara semua pembolehubah input dalam. 
Seperti yang ditunjukkan dalam Rajah 4(a), kita boleh memahami DAN di atas atau interaksi seperti ini: Kita boleh berfikir bahawa interaksi setara DAN mewakili "hubungan DAN" antara pembolehubah input dalam  yang dikodkan oleh rangkaian saraf. Sebagai contoh, diberikan ayat input
yang dikodkan oleh rangkaian saraf. Sebagai contoh, diberikan ayat input  , rangkaian saraf mungkin memodelkan interaksi antara
, rangkaian saraf mungkin memodelkan interaksi antara  sehingga
sehingga  menghasilkan utiliti berangka yang memacu "hujan hujan" keluaran rangkaian saraf. Jika sebarang pembolehubah input dalam
menghasilkan utiliti berangka yang memacu "hujan hujan" keluaran rangkaian saraf. Jika sebarang pembolehubah input dalam  terhalang, utiliti berangka itu akan dialih keluar daripada output rangkaian saraf. Begitu juga, kesetaraan atau interaksi
terhalang, utiliti berangka itu akan dialih keluar daripada output rangkaian saraf. Begitu juga, kesetaraan atau interaksi  mewakili "hubungan ATAU" antara pembolehubah input dalam
mewakili "hubungan ATAU" antara pembolehubah input dalam  yang dimodelkan oleh rangkaian saraf. Contohnya, diberikan ayat input
yang dimodelkan oleh rangkaian saraf. Contohnya, diberikan ayat input  , selagi mana-mana perkataan dalam
, selagi mana-mana perkataan dalam  muncul, ia akan memacu keluaran rangkaian saraf untuk mengklasifikasikan emosi negatif.
muncul, ia akan memacu keluaran rangkaian saraf untuk mengklasifikasikan emosi negatif. Interaksi setara yang dimodelkan oleh rangkaian saraf memenuhi tiga kriteria aksiomatik "konsep ideal", iaitu pemasangan tak terhingga, keterlanjuran dan kebolehpindahan antara sampel. Pemasangan tak terhingga: Seperti yang ditunjukkan dalam Rajah 4 dan 5, untuk sebarang sampel oklusi, output rangkaian saraf pada sampel boleh dipasang dengan jumlah utiliti konsep interaksi yang berbeza. Iaitu, kita boleh membina model logik berdasarkan interaksi Tidak kira bagaimana kita menyekat sampel input, model logik ini masih boleh menyesuaikan dengan tepat nilai output model dalam mana-mana keadaan sampel input yang disekat. Sparsity: Rangkaian saraf untuk tugas klasifikasi selalunya hanya memodelkan sebilangan kecil konsep interaktif yang penting, dan kebanyakan konsep interaktif adalah hingar dengan utiliti berangka hampir 0. Kebolehpindahan antara sampel: Interaksi boleh dipindahkan antara sampel yang berbeza, iaitu, konsep interaksi penting yang dimodelkan oleh rangkaian saraf pada sampel yang berbeza (dari kategori yang sama) selalunya mempunyai pertindihan yang hebat.

Rajah 4: Logik penaakulan kompleks rangkaian saraf boleh dipasang dengan tepat oleh model logik berdasarkan sebilangan kecil interaksi  . Setiap interaksi ialah ukuran hubungan tak linear antara rangkaian saraf yang memodelkan set pembolehubah input tertentu
. Setiap interaksi ialah ukuran hubungan tak linear antara rangkaian saraf yang memodelkan set pembolehubah input tertentu  . Apabila dan hanya apabila pembolehubah dalam set muncul pada masa yang sama, ia akan mencetuskan dan berinteraksi, dan menyumbang skor berangka kepada output
. Apabila dan hanya apabila pembolehubah dalam set muncul pada masa yang sama, ia akan mencetuskan dan berinteraksi, dan menyumbang skor berangka kepada output  Apabila mana-mana pembolehubah dalam set
Apabila mana-mana pembolehubah dalam set  muncul, ia akan mencetuskan atau berinteraksi.
muncul, ia akan mencetuskan atau berinteraksi. 
Rajah 5: Output rangkaian saraf pada mana-mana sampel oklusi boleh dipasang dengan jumlah utiliti konsep interaksi yang berbeza, iaitu, kita boleh membina model logik berdasarkan interaksi, tidak kira bagaimana kita menutup input sampel, walaupun kita miskin Contohnya, memandangkan kaedah oklusi yang berbeza sama sekali pada unit input, model logik ini masih boleh memuatkan nilai output sampel input model dengan tepat dalam sebarang keadaan oklusi. 5. Penemuan dan bukti baharu 5.1 Temui fenomena dua peringkat perubahan interaktif dalam rangkaian saraf semasa latihan , Kami memberi tumpuan kepada isu asas dalam bidang kebolehtafsiran rangkaian saraf, iaitu, cara meramalkan dengan tegas perubahan dalam keupayaan generalisasi rangkaian saraf semasa proses latihan dari perspektif analisis analitik, dan menganalisis peralihan rangkaian saraf daripada kurang kemas kepada lampiran dengan tepat. Keseluruhan proses perubahan dinamik pemasangan dan punca di sebaliknya
.Pertama, kami mentakrifkan susunan (kerumitan) interaksi sebagai bilangan pembolehubah input dalam interaksi, . Kerja pasukan kami sebelum ini mendapati bahawa kerumitan "interaksi dengan atau" yang dimodelkan oleh rangkaian saraf dalam sampel tertentu secara langsung menentukan keupayaan generalisasi rangkaian saraf dalam sampel ini [1], iaitu, tahap urutan tinggi saraf. pemodelan rangkaian. "interaksi AND-OR" (antara sejumlah besar unit input) cenderung mempunyai keupayaan generalisasi yang lemah, manakala interaksi "AND-OR" tertib rendah (antara sebilangan kecil unit input) mempunyai keupayaan generalisasi yang kuat. . kita boleh Keupayaan generalisasi rangkaian saraf pada peringkat yang berbeza dijelaskan melalui pengedaran pesanan berbeza "DAN atau interaksi" yang dimodelkan oleh rangkaian saraf pada titik masa yang berbeza. Untuk definisi keupayaan generalisasi interaksi dan definisi keupayaan generalisasi keseluruhan rangkaian saraf, sila rujuk bab "5.2 Hubungan antara susunan interaksi yang dimodelkan oleh rangkaian saraf dan keupayaan generalisasinya". 
untuk mengukur kekuatan semua interaksi signifikan positif tertib, dan , di mana
untuk mengukur kekuatan semua interaksi signifikan negatif tertibdan mewakili set interaksi penting, dan mewakili ambang signifikan. interaksi. Rajah 6: Kekuatan interaksi tertib yang berbeza  dan
dan  diekstrak daripada rangkaian saraf yang dilatih untuk pusingan berbeza. Proses latihan rangkaian saraf yang berbeza yang dilatih pada set data yang berbeza dan tugas yang berbeza mempunyai fenomena dua peringkat. Dua titik masa pertama yang dipilih tergolong dalam fasa pertama, manakala dua titik masa terakhir tergolong dalam fasa kedua. Tepat sejurus selepas memasuki peringkat kedua proses latihan rangkaian saraf, jurang kerugian antara kehilangan ujian dan kehilangan latihan rangkaian saraf mula meningkat dengan ketara (lihat lajur terakhir). Ini menunjukkan bahawa fenomena dua peringkat latihan rangkaian saraf "diselaraskan" dalam masa dengan perubahan dalam jurang kehilangan model. Sila lihat kertas untuk lebih banyak hasil percubaan.
diekstrak daripada rangkaian saraf yang dilatih untuk pusingan berbeza. Proses latihan rangkaian saraf yang berbeza yang dilatih pada set data yang berbeza dan tugas yang berbeza mempunyai fenomena dua peringkat. Dua titik masa pertama yang dipilih tergolong dalam fasa pertama, manakala dua titik masa terakhir tergolong dalam fasa kedua. Tepat sejurus selepas memasuki peringkat kedua proses latihan rangkaian saraf, jurang kerugian antara kehilangan ujian dan kehilangan latihan rangkaian saraf mula meningkat dengan ketara (lihat lajur terakhir). Ini menunjukkan bahawa fenomena dua peringkat latihan rangkaian saraf "diselaraskan" dalam masa dengan perubahan dalam jurang kehilangan model. Sila lihat kertas untuk lebih banyak hasil percubaan. Seperti yang ditunjukkan dalam Rajah 6, fenomena dua peringkat rangkaian saraf dimanifestasikan secara khusus sebagai: latihan neural awal, awalan awal - interaksi tahap, Interaksi tertib tinggi dan rendah jarang dikodkan, dan pengedaran interaksi tertib berbeza nampaknya "berbentuk gelendong." Dengan mengandaikan bahawa rangkaian saraf dengan parameter permulaan rawak memodelkan bunyi tulen, kami membuktikan dalam "5.4 Bukti Teori bagi Fenomena Dua Peringkat" bahawa taburan interaksi pesanan berbeza yang dimodelkan oleh rangkaian saraf dengan parameter permulaan rawak membentangkan "bentuk gelendong. ", Iaitu, hanya sebilangan kecil interaksi tertib rendah dan tinggi yang dimodelkan dan sebilangan besar interaksi tertib pertengahan dimodelkan.
- , kekuatan interaksi pesanan tinggi dan pertengahan yang dikodkan oleh rangkaian saraf beransur-ansur lemah, manakala kekuatan interaksi pesanan rendah secara beransur-ansur meningkat. Akhirnya, interaksi tertib tinggi dan pertengahan dihapuskan secara beransur-ansur, dan rangkaian saraf mengekod hanya interaksi tertib rendah.
Fenomena dua peringkat di atas wujud secara meluas dalam proses latihan rangkaian saraf dengan struktur berbeza pada set data berbeza pada tugasan berbeza
. Kami melatih VGG-11/13/16 pada set data imej (set data CIFAR-10, set data MNIST, set data CUB200-2011 (menggunakan imej burung yang dipangkas daripada gambar) dan set data Tiny-ImageNet) dan AlexNet. Kami melatih model Bert-Medium/Tiny untuk klasifikasi semantik sentimen pada dataset SST-2, dan kami melatih DGCNN pada dataset ShapeNet untuk mengklasifikasikan data awan titik 3D. Rajah di atas menunjukkan taburan interaksi penting bagi pesanan berbeza yang diekstrak oleh rangkaian saraf yang berbeza pada zaman latihan yang berbeza. Kami telah menemui fenomena dua peringkat semasa proses latihan rangkaian saraf ini. Sila rujuk kertas untuk lebih banyak keputusan dan butiran eksperimen.5.2 Hubungan antara susunan interaksi yang dimodelkan oleh rangkaian saraf dan kebolehan generalisasinya
Kerja pasukan kami sebelum ini telah menemui susunan interaksi yang dimodelkan oleh rangkaian saraf, iaitu hubungan Kebolehan generalisasi. , interaksi peringkat tinggi mempunyai keupayaan generalisasi yang lebih teruk daripada interaksi peringkat rendah [1]. Kebolehgeneralisasian interaksi khusus ditakrifkan dengan jelas - jika interaksi kerap dimodelkan oleh rangkaian saraf dalam kedua-dua sampel latihan dan sampel ujian, maka interaksi ini mempunyai keupayaan generalisasi yang baik. Dalam artikel Zhihu ini, dua eksperimen diperkenalkan untuk membuktikan bahawa interaksi tertib tinggi mempunyai keupayaan generalisasi yang lemah, dan interaksi tertib rendah mempunyai keupayaan generalisasi yang kuat.🎜🎜Percubaan 1: Perhatikan generalisasi interaksi yang dimodelkan oleh rangkaian saraf berbeza yang dilatih pada set data berbeza. Di sini kami menggunakan persamaan Jaccard antara taburan interaksi yang dicetuskan oleh set ujian dan taburan interaksi yang dicetuskan oleh set latihan untuk mengukur generalisasi interaksi🎜.Khususnya, diberikan sampel input dalam tugas pengelasan. kebolehan generalisasi interaksi tertib, iaitu: yang mengandungi
yang mengandungi  pembolehubah input, kami vektorkan
pembolehubah input, kami vektorkan  interaksi
interaksi  -tertib yang diekstrak daripada sampel input
-tertib yang diekstrak daripada sampel input  , di mana
, di mana  mewakili
mewakili 
 interaksi tertib. Kemudian, kami mengira purata vektor interaksi pesanan
interaksi tertib. Kemudian, kami mengira purata vektor interaksi pesanan  yang diekstrak daripada semua sampel dengan kategori
yang diekstrak daripada semua sampel dengan kategori  dalam tugas pengelasan, dinyatakan sebagai
dalam tugas pengelasan, dinyatakan sebagai  , dengan
, dengan  mewakili set sampel dengan kategori
mewakili set sampel dengan kategori  .Seterusnya, kami mengira persamaan Jaccard antara vektor interaksi purata
.Seterusnya, kami mengira persamaan Jaccard antara vektor interaksi purata  susunan
susunan  yang diekstrak daripada sampel latihan dan vektor interaksi purata
yang diekstrak daripada sampel latihan dan vektor interaksi purata  susunan
susunan  yang diekstrak daripada sampel ujian untuk mengukur
yang diekstrak daripada sampel ujian untuk mengukur  sampel dengan kategori
sampel dengan kategori 
 di mana,
di mana,  dan
dan  menayangkan dua vektor interaksi
menayangkan dua vektor interaksi  -dimensi pada dua
-dimensi pada dua  Kami menjalankan eksperimen untuk mengira interaksi pesanan yang berbeza
Kami menjalankan eksperimen untuk mengira interaksi pesanan yang berbeza . Kami menguji LeNet yang dilatih pada dataset MNIST, VGG-11 dilatih pada dataset CIFAR-10, VGG-13 dilatih pada dataset CUB200-2011 dan AlexNet dilatih pada dataset Tiny-ImageNet. Untuk mengurangkan kos pengiraan, kami hanya mengira purata persamaan Jaccard bagi 10 kategori teratas
. Kami menguji LeNet yang dilatih pada dataset MNIST, VGG-11 dilatih pada dataset CIFAR-10, VGG-13 dilatih pada dataset CUB200-2011 dan AlexNet dilatih pada dataset Tiny-ImageNet. Untuk mengurangkan kos pengiraan, kami hanya mengira purata persamaan Jaccard bagi 10 kategori teratas
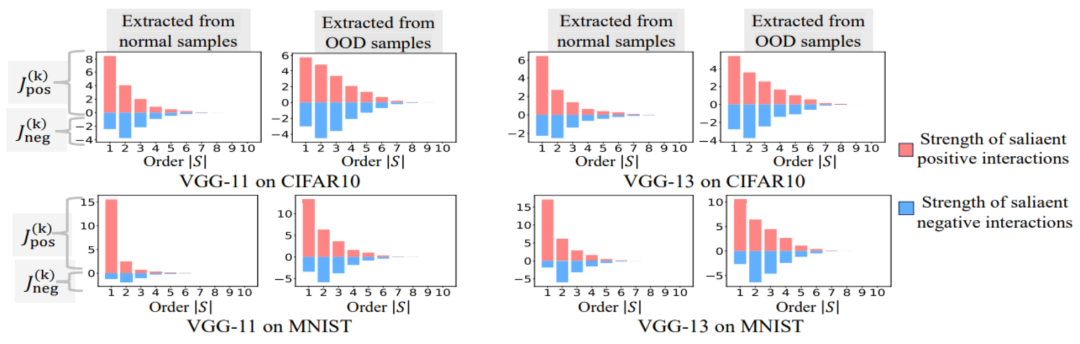
Experiment 2: Vergleich der Verteilung von Interaktionen, die durch neuronale Netze an normalen Proben und OOD-Proben modelliert wurden. Wir verglichen Interaktionen, die aus normalen Proben extrahiert wurden, mit Interaktionen, die aus Proben außerhalb der Verteilung (OOD) extrahiert wurden, um zu untersuchen, ob das neuronale Netzwerk mehr Interaktionen höherer Ordnung auf OOD-Proben modelliert. Wir haben die Klassifizierungsbezeichnungen einer kleinen Anzahl von Trainingsbeispielen auf falsche Bezeichnungen gesetzt. Auf diese Weise können die Originalproben im Datensatz als normale Proben betrachtet werden, während einige Proben mit falschen Bezeichnungen OOD-Proben entsprechen und diese OOD-Proben zu einer Überanpassung des neuronalen Netzwerks führen können. Wir haben VGG-11 und VGG-13 anhand des MNIST-Datensatzes bzw. des CIFAR-10-Datensatzes trainiert. Abbildung 8 vergleicht die Verteilung der aus normalen Proben extrahierten Interaktionen mit der Verteilung der aus OOD-Proben extrahierten Interaktionen. Wir stellen fest, dass VGG-11 und VGG-13 komplexere Wechselwirkungen (Wechselwirkungen höherer Ordnung) bei der Klassifizierung von OOD-Proben modellieren, während Wechselwirkungen niedrigerer Ordnung bei der Klassifizierung normaler Proben verwendet werden. Dies bestätigt, dass die Generalisierungsfähigkeit von Wechselwirkungen höherer Ordnung im Allgemeinen schwächer ist als die von Wechselwirkungen niedrigerer Ordnung.
常 Abbildung 8: Vergleichen Sie Interaktionen, die aus normalen Stichproben extrahiert wurden, und Interaktionen, die aus Verteilungsstichproben (OOD) extrahiert wurden. Neuronale Netze modellieren typischerweise Interaktionen höherer Ordnung an OOD-Proben. 5.3 Das zweistufige Phänomen und die Änderung der Verlustlücke während des Trainingsprozesses des neuronalen Netzes sind relativ konsistent Dynamik des neuronalen Netzwerks. Ein sehr interessantes Phänomen besteht darin, dass das zweistufige Phänomen im Trainingsprozess des neuronalen Netzwerks und die Änderungen der Verlustlücke des neuronalen Netzwerks im Testsatz und im Trainingssatz zeitlich aufeinander abgestimmt sind
. Die Verlustlücke zwischen Trainingsverlust und Testverlust ist die am häufigsten verwendete Metrik zur Messung des Grads der Modellüberanpassung. Abbildung 6 zeigt die Kurven der Verlustlücke zwischen dem Testverlust und dem Trainingsverlust des Trainingsprojekts für verschiedene neuronale Netze sowie die aus den neuronalen Netzen extrahierten Interaktionsverteilungen in verschiedenen Trainingsepochen. Wir haben festgestellt, dass, wenn die Verlustlücke zwischen dem Testverlust und dem Trainingsverlust während des Trainingsprozesses des neuronalen Netzwerks zuzunehmen beginnt, das neuronale Netzwerk zufällig in die zweite Trainingsphase eintritt. Dies zeigt, dass das zweistufige Phänomen des neuronalen Netzwerktrainings zeitlich an Änderungen der Modellverlustlücke „ausgerichtet“ wird. Wir können das obige Phänomen folgendermaßen verstehen: Bevor der Trainingsprozess beginnt, stellen alle vom initialisierten neuronalen Netzwerk modellierten Interaktionen zufälliges Rauschen dar, und die Verteilung der Interaktionen unterschiedlicher Ordnung sieht aus wie eine „Spindel“. In der ersten Phase des neuronalen Netzwerktrainings eliminiert das neuronale Netzwerk nach und nach Interaktionen mittlerer und höherer Ordnung und lernt die einfachsten Interaktionen (niedrigster Ordnung). Anschließend modelliert das neuronale Netzwerk in der zweiten Phase des neuronalen Netzwerktrainings Interaktionen zunehmender Ordnung. Da unsere beiden Experimente im Kapitel „5.2 Die Beziehung zwischen der durch neuronale Netze modellierten Interaktionsreihenfolge und ihrer Generalisierungsfähigkeit“ bestätigt haben, dass Interaktionen höherer Ordnung normalerweise schlechtere Generalisierungsfähigkeiten aufweisen als Interaktionen niedriger Ordnung, können wir darüber nachdenken In der zweiten Stufe Beim Training neuronaler Netze lernt das DNN zunächst die Interaktionen mit der stärksten Generalisierungsfähigkeit und geht dann schrittweise zu komplexeren Interaktionen mit schwächerer Generalisierungsfähigkeit über. Mit der Zeit überpassen einige neuronale Netze nach und nach und kodieren eine große Anzahl von Interaktionen mittlerer und höherer Ordnung.5.4 Theoretisch beweisen Sie das zweistufige Phänomen. Theoretisch beweisen Sie, dass das zweistufige Phänomen des neuronalen Netzwerktrainingsprozesses in drei Teile unterteilt ist Zufällig initialisiertes neuronales Netzwerk vor Beginn des Trainingsprozesses. Die Verteilung der modellierten Interaktionen weist eine „Spindelform“ auf, das heißt, Interaktionen hoher und niedriger Ordnung werden selten modelliert, und Interaktionen mittlerer Ordnung werden hauptsächlich modelliert. Der zweite Teil zeigt, dass das neuronale Netzwerk in der zweiten Trainingsphase immer größere Interaktionen modelliert. Abschnitt 3 zeigt, dass das neuronale Netzwerk in der ersten Trainingsphase nach und nach Interaktionen mittlerer und hoher Ordnung eliminiert und die Interaktionen mit den niedrigsten Kosten lernt. 1. Beweisen Sie die „Spindel“-Interaktionsverteilung für die Initialisierung neuronaler Netzwerkmodellierung. Da die zufällig initialisierten Zufallsnetzwerkmodelle vor Beginn des Trainingsprozesses Rauschen erzeugen, gehen wir davon aus, dass die vom zufällig initialisierten neuronalen Netzwerk modellierten Interaktionen der Normalverteilung mit Mittelwert und Varianz gehorchen. Unter den oben genannten Annahmen konnten wir zeigen, dass die Verteilung der Intensitätssumme der Interaktionen, die vom initialisierten neuronalen Netzwerk modelliert wird, eine „Spindelform“ aufweist, d. h. es modelliert selten Interaktionen hoher und niedriger Ordnung und hauptsächlich mittlere Interaktionen bestellen.2. Beweisen Sie den dynamischen Prozess interaktiver Veränderungen in der zweiten Stufe des neuronalen Netzwerktrainings. Bevor wir an der formellen Zertifizierung teilnehmen, müssen wir die folgenden vorbereitenden Arbeiten durchführen. Zunächst folgen wir dem Ansatz von [5, 6] und schreiben die Inferenz des neuronalen Netzwerks  auf eine bestimmte Stichprobe als gewichtete Summe verschiedener Interaktionsauslösefunktionen um:
auf eine bestimmte Stichprobe als gewichtete Summe verschiedener Interaktionsauslösefunktionen um:  wobei
wobei  ein Skalargewicht ist, das
ein Skalargewicht ist, das  erfüllt. Die Funktion
erfüllt. Die Funktion  ist eine interaktive Triggerfunktion, die
ist eine interaktive Triggerfunktion, die  bei jeder Okklusionsprobe
bei jeder Okklusionsprobe  erfüllt. Die spezifische Form der Funktion
erfüllt. Die spezifische Form der Funktion  kann aus der Taylor-Erweiterung abgeleitet werden. Bitte beziehen Sie sich auf das Papier und werden hier nicht beschrieben.
kann aus der Taylor-Erweiterung abgeleitet werden. Bitte beziehen Sie sich auf das Papier und werden hier nicht beschrieben. Gemäß der oben umgeschriebenen Form Das Lernen des neuronalen Netzwerks an einer bestimmten Probe kann ungefähr als das Lernen des Gewichts  der interaktiven Triggerfunktion angesehen werden. Darüber hinaus ergab die Vorarbeit des Labors [3], dass verschiedene neuronale Netze, die vollständig auf dieselbe Aufgabe trainiert sind, dazu neigen, ähnliche Interaktionen zu modellieren, sodass wir das Lernen neuronaler Netze als eine Reihe potenzieller Grundwahrheitsinteraktionen betrachten können. Daher kann die Interaktion, die vom neuronalen Netzwerk modelliert wird, wenn es auf Konvergenz trainiert wird, als die Lösung angesehen werden, die man erhält, wenn man die folgende Zielfunktion minimiert:
der interaktiven Triggerfunktion angesehen werden. Darüber hinaus ergab die Vorarbeit des Labors [3], dass verschiedene neuronale Netze, die vollständig auf dieselbe Aufgabe trainiert sind, dazu neigen, ähnliche Interaktionen zu modellieren, sodass wir das Lernen neuronaler Netze als eine Reihe potenzieller Grundwahrheitsinteraktionen betrachten können. Daher kann die Interaktion, die vom neuronalen Netzwerk modelliert wird, wenn es auf Konvergenz trainiert wird, als die Lösung angesehen werden, die man erhält, wenn man die folgende Zielfunktion minimiert:  wobei
wobei  eine Reihe potenzieller Grundwahrheitsinteraktionen darstellt, die das neuronale Netzwerk anpassen muss.
eine Reihe potenzieller Grundwahrheitsinteraktionen darstellt, die das neuronale Netzwerk anpassen muss.  und
und  stellen jeweils den Vektor dar, der durch Zusammenfügen aller Gewichte erhalten wird, und den Vektor, der durch Zusammenfügen der Werte aller Interaktionsauslösefunktionen erhalten wird.
stellen jeweils den Vektor dar, der durch Zusammenfügen aller Gewichte erhalten wird, und den Vektor, der durch Zusammenfügen der Werte aller Interaktionsauslösefunktionen erhalten wird. Obwohl die obige Modellierung die Interaktion erhalten kann, wenn das neuronale Netzwerk auf Konvergenz trainiert wird, kann sie leider den dynamischen Prozess der Lerninteraktion während des Trainingsprozesses des neuronalen Netzwerks nicht gut beschreiben. Hier stellen wir unsere Kernhypothese vor: Wir gehen davon aus, dass die Parameter des initialisierten neuronalen Netzwerks eine große Menge an Rauschen enthalten und die Stärke dieser Rauschen während des Trainingsprozesses allmählich kleiner wird. Darüber hinaus führt Rauschen bei den Parametern zu Rauschen bei der Interaktionstriggerfunktion , und dieses Rauschen nimmt exponentiell mit der Interaktionsreihenfolge zu (dies wurde in [5] experimentell beobachtet und verifiziert). Wir modellieren das Lernen neuronaler Netze mit Rauschen wie folgt: 
wo Lärm  befriedigt
befriedigt  . Und mit fortschreitendem Training wird die Varianz des Rauschens
. Und mit fortschreitendem Training wird die Varianz des Rauschens  allmählich kleiner.
allmählich kleiner. Durch Minimieren der obigen Verlustfunktion für einen gegebenen Geräuschpegel  kann die analytische Lösung des optimalen Interaktionsgewichts
kann die analytische Lösung des optimalen Interaktionsgewichts  erhalten werden, wie im Satz in der Abbildung unten gezeigt.
erhalten werden, wie im Satz in der Abbildung unten gezeigt. 
Wir haben festgestellt, dass mit fortschreitendem Training (d. h. die Rauschgröße  kleiner wird) das Verhältnis von Interaktionsstärken niedriger und mittlerer Ordnung zu Interaktionsstärken hoher Ordnung allmählich abnimmt (wie in der Abbildung gezeigt). Satz unten). Dies erklärt das Phänomen, dass das neuronale Netzwerk in der zweiten Trainingsphase nach und nach Interaktionen höherer Ordnung lernt.
kleiner wird) das Verhältnis von Interaktionsstärken niedriger und mittlerer Ordnung zu Interaktionsstärken hoher Ordnung allmählich abnimmt (wie in der Abbildung gezeigt). Satz unten). Dies erklärt das Phänomen, dass das neuronale Netzwerk in der zweiten Trainingsphase nach und nach Interaktionen höherer Ordnung lernt. 
Darüber hinaus haben wir die obige Schlussfolgerung experimentell weiter überprüft. Bei einer Stichprobe mit n Eingabeeinheiten kann die Metrik  , wobei
, wobei  , verwendet werden, um näherungsweise das Verhältnis der Stärke der Wechselwirkung k-ter Ordnung zur Wechselwirkung k+1-ter Ordnung zu messen. In der folgenden Abbildung können wir feststellen, dass bei unterschiedlicher Anzahl von Eingabeeinheiten n und unterschiedlichen Ordnungen k das Verhältnis mit abnehmendem
, verwendet werden, um näherungsweise das Verhältnis der Stärke der Wechselwirkung k-ter Ordnung zur Wechselwirkung k+1-ter Ordnung zu messen. In der folgenden Abbildung können wir feststellen, dass bei unterschiedlicher Anzahl von Eingabeeinheiten n und unterschiedlichen Ordnungen k das Verhältnis mit abnehmendem  allmählich abnimmt.
allmählich abnimmt. 
Abbildung 9: Bei unterschiedlicher Anzahl von Eingabeeinheiten n und unterschiedlicher Ordnung k ändert sich das Verhältnis der Wechselwirkung k-ter Ordnung und der Wechselwirkungsstärke k+1-ter Ordnung mit dem Rauschpegel  und nimmt allmählich ab . Dies zeigt, dass mit fortschreitendem Training (d. h.
und nimmt allmählich ab . Dies zeigt, dass mit fortschreitendem Training (d. h.  wird allmählich kleiner) das Verhältnis der Interaktionsintensität niedriger Ordnung zur Interaktionsintensität hoher Ordnung allmählich kleiner wird und das neuronale Netzwerk allmählich Interaktionen höherer Ordnung lernt.
wird allmählich kleiner) das Verhältnis der Interaktionsintensität niedriger Ordnung zur Interaktionsintensität hoher Ordnung allmählich kleiner wird und das neuronale Netzwerk allmählich Interaktionen höherer Ordnung lernt. Abschließend verglichen wir die Verteilung der theoretischen Interaktionswerte bei jeder Reihenfolge unter unterschiedlichen Geräuschpegeln 
 mit der Verteilung jeder Interaktionsreihenfolge während des tatsächlichen Trainingsprozesses
mit der Verteilung jeder Interaktionsreihenfolge während des tatsächlichen Trainingsprozesses  und stellten fest, dass die Theorie: Die Interaktionsverteilung kann die Interaktionsintensitätsverteilung zu jedem Zeitpunkt im tatsächlichen Training gut vorhersagen.
und stellten fest, dass die Theorie: Die Interaktionsverteilung kann die Interaktionsintensitätsverteilung zu jedem Zeitpunkt im tatsächlichen Training gut vorhersagen. 

Abbildung 10: Vergleich der theoretischen Interaktionsverteilung  (blaues Histogramm) und der tatsächlichen Interaktionsverteilung
(blaues Histogramm) und der tatsächlichen Interaktionsverteilung  (oranges Histogramm). Die theoretische Interaktionsverteilung sagt die tatsächliche Interaktionsverteilung zu verschiedenen Zeitpunkten in der zweiten Trainingsphase gut voraus und passt sie an. Weitere Ergebnisse finden Sie im Papier.
(oranges Histogramm). Die theoretische Interaktionsverteilung sagt die tatsächliche Interaktionsverteilung zu verschiedenen Zeitpunkten in der zweiten Trainingsphase gut voraus und passt sie an. Weitere Ergebnisse finden Sie im Papier. 3. Beweisen Sie den dynamischen Prozess interaktiver Veränderungen in der ersten Stufe des neuronalen Netzwerktrainings. Wenn die dynamische Änderung der Interaktion in der zweiten Trainingsstufe als Änderung der optimalen Gewichtslösung  erklärt werden kann, wenn der Lärm
erklärt werden kann, wenn der Lärm  allmählich abnimmt, dann kann die erste Stufe sein Betrachtet als Interaktion von Die anfängliche zufällige Interaktion konvergiert allmählich zur optimalen Lösung.
allmählich abnimmt, dann kann die erste Stufe sein Betrachtet als Interaktion von Die anfängliche zufällige Interaktion konvergiert allmählich zur optimalen Lösung. Es liegt noch ein langer Weg vor uns. Wir arbeiten an den ersten Prinzipien der Interpretierbarkeit neuronaler Netze. Wir hoffen, diese Theorie in weiteren Aspekten zu verankern und strikt beweisen zu können, dass äquivalente Interaktionen eine symbolische Erklärung sind. und kann die Verallgemeinerung und Robustheit neuronaler Netze erklären, gleichzeitig den Flaschenhals der Darstellung neuronaler Netze nachweisen, 12 Methoden zur Verbesserung der Widerstandsfähigkeit neuronaler Netze gegen Migration vereinheitlichen und 14 Methoden zur Wichtigkeitsschätzung erklären. Wir werden später weitere solide Arbeit leisten, um das theoretische System weiter zu verbessern. [1] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan und Quanshi Zhang. Erklären Sie die Verallgemeinerungskraft eines DNN mithilfe interaktiver Konzepte [2] Arthur Jacot, Franck Gabriel, Clement Hongler. Konvergenz und Generalisierung in neuronalen Netzen, 2018 [3] Kodiert ein neuronales Netz wirklich symbolische Konzepte? , 2023 [4] Wen Shen, Lei Cheng, Yuxiao Yang, Mingjie Li und Quanshi Zhang. Kann die Inferenzlogik großer Sprachmodelle in symbolische Konzepte entwirrt werden? [5] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou und Quanshi Zhang. Bayesianische neuronale Netze neigen dazu, komplexe und sensible Konzepte zu ignorieren Zhang. Auf dem Weg zur Schwierigkeit eines tiefen neuronalen Netzwerks, Konzepte unterschiedlicher Komplexität zu lernen. Ziwei Yang, Zheyang Li und Quanshi Zhang. Vereinheitlichung von vierzehn Post-Hoc-Attributionsmethoden mit Taylor-Interaktionen (IEEE T-PAMI), 2024. [2] Xu Cheng, Lei Cheng , Zhaoran Peng, Yang Xu, Tian Han und Quanshi Zhang. [3] Qihan Ren, Jiayang Gao, Wen Shen und Quanshi Zhang im Nachweis der Entstehung spärlicher Interaktionsprimitive in KI-Modellen. [4] Definition und Extraktion generalisierbarer Interaktionsprimitive aus DNNs.
[5] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan und Quanshi Zhang. Erklären Sie die Generalisierungskraft eines DNN mithilfe interaktiver Konzepte.
[ 6 ] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang und Quanshi Zhang. Auf dem Weg zur Schwierigkeit, Konzepte unterschiedlicher Komplexität für ein tiefes neuronales Netzwerk zu lernen
[7] Quanshi Zhang, Jie Ren, Ge Huang, Ruiming Cao, Ying Nian Wu und Song-Chun Zhu. Gewinnung interpretierbarer AOG-Darstellungen aus Faltungsnetzwerken über aktive Fragebeantwortung (IEEE T -PAMI), 2020.
[8] Xin Wang, Jie Ren, Shuyun Lin, Xiangming Zhu, Yisen Wang und Quanshi Zhang. Ein einheitlicher Ansatz zur Interpretation und Steigerung der kontradiktorischen Übertragbarkeit [9] Hao Zhang, Sen Li, Yinchao Ma, Mingjie Li, Yichen Xie und Quanshi Zhang . Kodiert ein neuronales Netzwerk wirklich ein symbolisches Konzept? . ICML, 2023.
[12] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou und Quanshi Zhang. Vermeiden Sie die Kodierung störungsempfindlicher und komplexer Konzepte ] Jie Ren, Mingjie Li, Qirui Chen, Huiqi Deng und Quanshi Zhang: Definition und Quantifizierung der Entstehung spärlicher Konzepte in DNNs, 2023.
[14] Jie Ren, Mingjie Li, Meng Zhou, Shih- Han Chan und Quanshi Zhang. Auf dem Weg zur theoretischen Analyse der Transformationskomplexität von ReLU-DNNs, 2022.
[15] Jie Ren, Die Zhang, Yisen Wang, Lu Chen, Zhanpeng Zhou, Yiting Chen, Xu Cheng, Xin Wang, Meng Zhou, Jie Shi und Quanshi Zhang. Eine einheitliche spieltheoretische Interpretation der gegnerischen Robustheit DNNs für die 3D-Punktwolkenverarbeitung.
[17] Xin Wang, Shuyun Lin, Hao Zhang, Yufei Zhu und Quanshi Zhang. ] Wen Shen, Zhihua Wei, Shikun Huang, Binbin Zhang, Panyue Chen, Ping Zhao und Quanshi Zhang: Interpreting Utilities of Network Architectures for 3D Point Cloud Processing, 2021.
[19] Hao Zhang, Yichen Xie , Longjie Zheng, Die Zhang und Quanshi Zhang. Interpreting Multivariate Shapley Interactions in DNNs, 2021. Mengyue Wu und Quanshi Zhang. Aufbau interpretierbarer Interaktionsbäume für Deep NLP-Modelle, 2021.
Atas ialah kandungan terperinci Persoalan utama kebolehjelasan ialah, apakah penjelasan pertama? 20 kertas CCF-A+ICLR memberi anda jawapan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Aliran teknologi untuk ditonton pada tahun 2023
- Cara Kecerdasan Buatan Membawa Kerja Baharu Setiap Hari kepada Pasukan Pusat Data
- Bolehkah kecerdasan buatan atau automasi menyelesaikan masalah kecekapan tenaga yang rendah dalam bangunan?
- Pengasas bersama OpenAI ditemu bual oleh Huang Renxun: Keupayaan penaakulan GPT-4 belum mencapai jangkaan
- Bing Microsoft mengatasi Google dalam trafik carian terima kasih kepada teknologi OpenAI


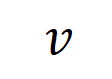
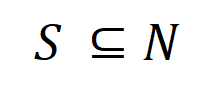 yang dikodkan oleh rangkaian saraf. Sebagai contoh, diberikan ayat input
yang dikodkan oleh rangkaian saraf. Sebagai contoh, diberikan ayat input 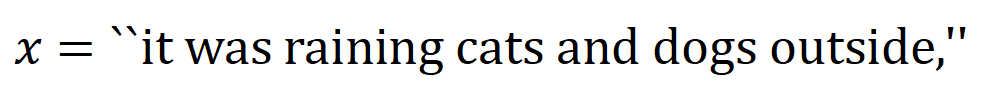 , rangkaian saraf mungkin memodelkan interaksi antara
, rangkaian saraf mungkin memodelkan interaksi antara 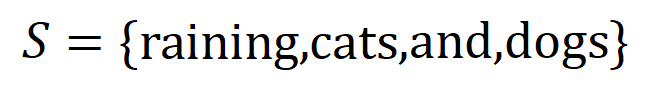 sehingga
sehingga 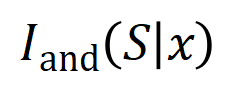 menghasilkan utiliti berangka yang memacu "hujan hujan" keluaran rangkaian saraf. Jika sebarang pembolehubah input dalam
menghasilkan utiliti berangka yang memacu "hujan hujan" keluaran rangkaian saraf. Jika sebarang pembolehubah input dalam 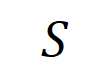 terhalang, utiliti berangka itu akan dialih keluar daripada output rangkaian saraf. Begitu juga, kesetaraan atau interaksi
terhalang, utiliti berangka itu akan dialih keluar daripada output rangkaian saraf. Begitu juga, kesetaraan atau interaksi 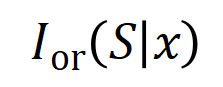 mewakili "hubungan ATAU" antara pembolehubah input dalam
mewakili "hubungan ATAU" antara pembolehubah input dalam  yang dimodelkan oleh rangkaian saraf. Contohnya, diberikan ayat input
yang dimodelkan oleh rangkaian saraf. Contohnya, diberikan ayat input 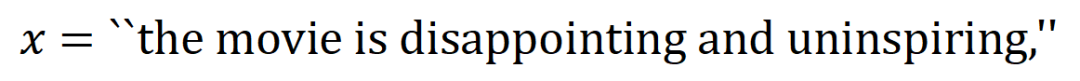 , selagi mana-mana perkataan dalam
, selagi mana-mana perkataan dalam 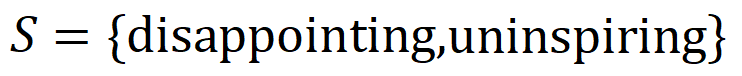 muncul, ia akan memacu keluaran rangkaian saraf untuk mengklasifikasikan emosi negatif.
muncul, ia akan memacu keluaran rangkaian saraf untuk mengklasifikasikan emosi negatif. 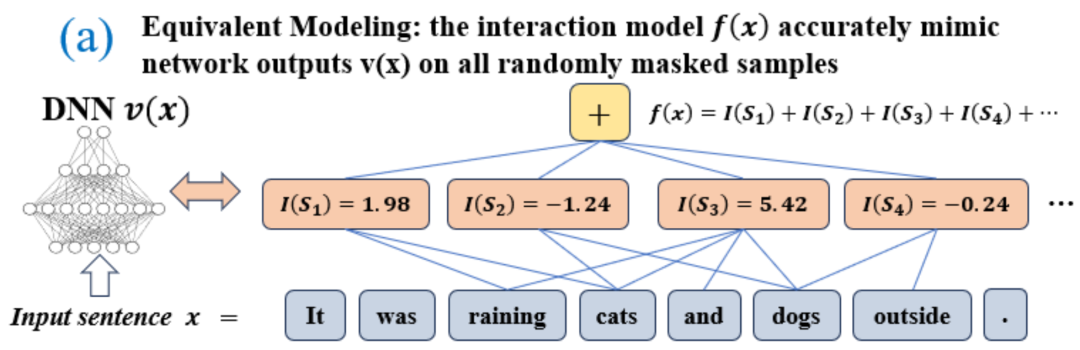
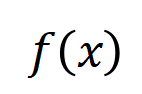 . Setiap interaksi ialah ukuran hubungan tak linear antara rangkaian saraf yang memodelkan set pembolehubah input tertentu
. Setiap interaksi ialah ukuran hubungan tak linear antara rangkaian saraf yang memodelkan set pembolehubah input tertentu 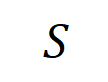 . Apabila dan hanya apabila pembolehubah dalam set muncul pada masa yang sama, ia akan mencetuskan dan berinteraksi, dan menyumbang skor berangka kepada output
. Apabila dan hanya apabila pembolehubah dalam set muncul pada masa yang sama, ia akan mencetuskan dan berinteraksi, dan menyumbang skor berangka kepada output 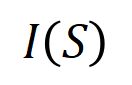 Apabila mana-mana pembolehubah dalam set
Apabila mana-mana pembolehubah dalam set  muncul, ia akan mencetuskan atau berinteraksi.
muncul, ia akan mencetuskan atau berinteraksi. 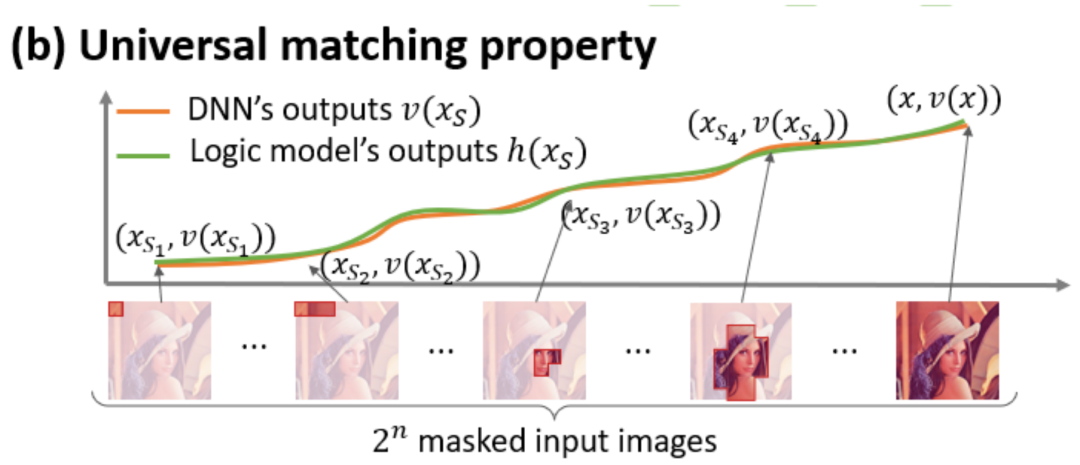
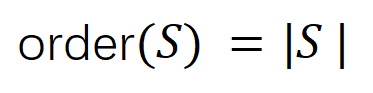
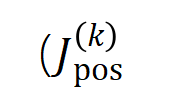 dan
dan 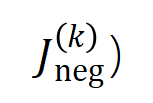 diekstrak daripada rangkaian saraf yang dilatih untuk pusingan berbeza. Proses latihan rangkaian saraf yang berbeza yang dilatih pada set data yang berbeza dan tugas yang berbeza mempunyai fenomena dua peringkat. Dua titik masa pertama yang dipilih tergolong dalam fasa pertama, manakala dua titik masa terakhir tergolong dalam fasa kedua. Tepat sejurus selepas memasuki peringkat kedua proses latihan rangkaian saraf, jurang kerugian antara kehilangan ujian dan kehilangan latihan rangkaian saraf mula meningkat dengan ketara (lihat lajur terakhir). Ini menunjukkan bahawa fenomena dua peringkat latihan rangkaian saraf "diselaraskan" dalam masa dengan perubahan dalam jurang kehilangan model. Sila lihat kertas untuk lebih banyak hasil percubaan.
diekstrak daripada rangkaian saraf yang dilatih untuk pusingan berbeza. Proses latihan rangkaian saraf yang berbeza yang dilatih pada set data yang berbeza dan tugas yang berbeza mempunyai fenomena dua peringkat. Dua titik masa pertama yang dipilih tergolong dalam fasa pertama, manakala dua titik masa terakhir tergolong dalam fasa kedua. Tepat sejurus selepas memasuki peringkat kedua proses latihan rangkaian saraf, jurang kerugian antara kehilangan ujian dan kehilangan latihan rangkaian saraf mula meningkat dengan ketara (lihat lajur terakhir). Ini menunjukkan bahawa fenomena dua peringkat latihan rangkaian saraf "diselaraskan" dalam masa dengan perubahan dalam jurang kehilangan model. Sila lihat kertas untuk lebih banyak hasil percubaan. 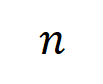 yang mengandungi
yang mengandungi  pembolehubah input, kami vektorkan
pembolehubah input, kami vektorkan  interaksi
interaksi  -tertib yang diekstrak daripada sampel input
-tertib yang diekstrak daripada sampel input 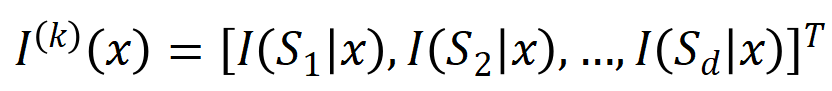 , di mana
, di mana 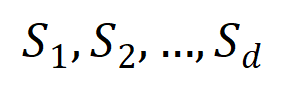 mewakili
mewakili 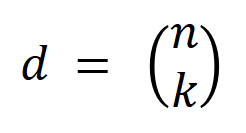
 interaksi tertib. Kemudian, kami mengira purata vektor interaksi pesanan
interaksi tertib. Kemudian, kami mengira purata vektor interaksi pesanan 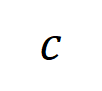 yang diekstrak daripada semua sampel dengan kategori
yang diekstrak daripada semua sampel dengan kategori 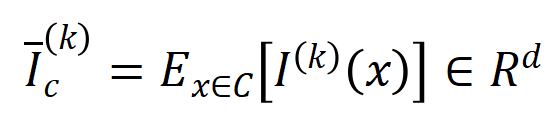 , dengan
, dengan 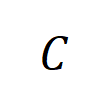 mewakili set sampel dengan kategori
mewakili set sampel dengan kategori  .Seterusnya, kami mengira persamaan Jaccard antara vektor interaksi purata
.Seterusnya, kami mengira persamaan Jaccard antara vektor interaksi purata 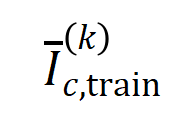 susunan
susunan 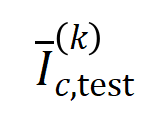 susunan
susunan 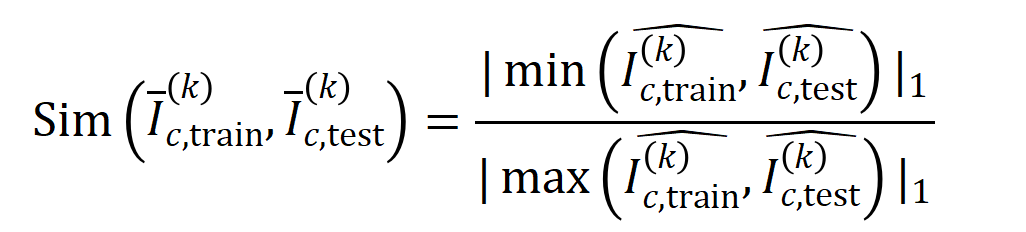
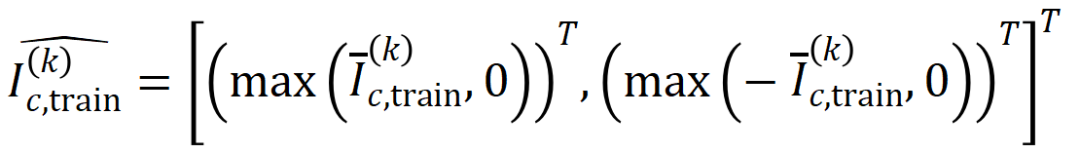 di mana,
di mana, 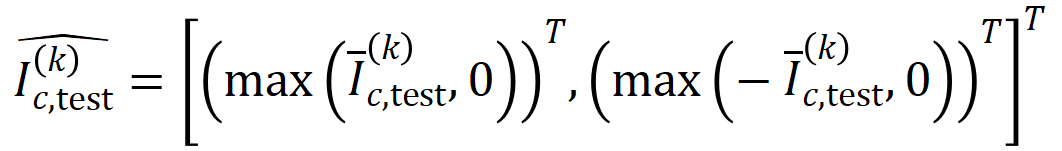 dan
dan 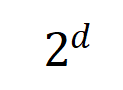 menayangkan dua vektor interaksi
menayangkan dua vektor interaksi 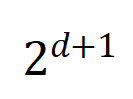 -dimensi pada dua
-dimensi pada dua 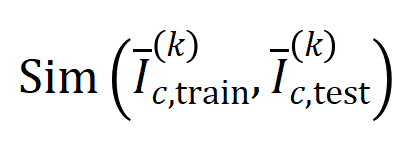 Kami menjalankan eksperimen untuk mengira interaksi pesanan yang berbeza
Kami menjalankan eksperimen untuk mengira interaksi pesanan yang berbeza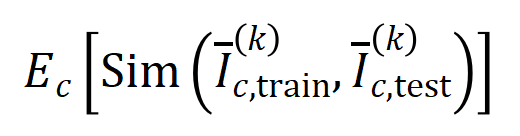 . Kami menguji LeNet yang dilatih pada dataset MNIST, VGG-11 dilatih pada dataset CIFAR-10, VGG-13 dilatih pada dataset CUB200-2011 dan AlexNet dilatih pada dataset Tiny-ImageNet. Untuk mengurangkan kos pengiraan, kami hanya mengira purata persamaan Jaccard bagi 10 kategori teratas
. Kami menguji LeNet yang dilatih pada dataset MNIST, VGG-11 dilatih pada dataset CIFAR-10, VGG-13 dilatih pada dataset CUB200-2011 dan AlexNet dilatih pada dataset Tiny-ImageNet. Untuk mengurangkan kos pengiraan, kami hanya mengira purata persamaan Jaccard bagi 10 kategori teratas
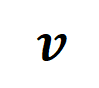 auf eine bestimmte Stichprobe als gewichtete Summe verschiedener Interaktionsauslösefunktionen um:
auf eine bestimmte Stichprobe als gewichtete Summe verschiedener Interaktionsauslösefunktionen um:  wobei
wobei  ein Skalargewicht ist, das
ein Skalargewicht ist, das  erfüllt. Die Funktion
erfüllt. Die Funktion  ist eine interaktive Triggerfunktion, die
ist eine interaktive Triggerfunktion, die  bei jeder Okklusionsprobe
bei jeder Okklusionsprobe  erfüllt. Die spezifische Form der Funktion
erfüllt. Die spezifische Form der Funktion  kann aus der Taylor-Erweiterung abgeleitet werden. Bitte beziehen Sie sich auf das Papier und werden hier nicht beschrieben.
kann aus der Taylor-Erweiterung abgeleitet werden. Bitte beziehen Sie sich auf das Papier und werden hier nicht beschrieben. 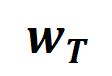 der interaktiven Triggerfunktion angesehen werden. Darüber hinaus ergab die Vorarbeit des Labors [3], dass verschiedene neuronale Netze, die vollständig auf dieselbe Aufgabe trainiert sind, dazu neigen, ähnliche Interaktionen zu modellieren, sodass wir das Lernen neuronaler Netze als eine Reihe potenzieller Grundwahrheitsinteraktionen betrachten können. Daher kann die Interaktion, die vom neuronalen Netzwerk modelliert wird, wenn es auf Konvergenz trainiert wird, als die Lösung angesehen werden, die man erhält, wenn man die folgende Zielfunktion minimiert:
der interaktiven Triggerfunktion angesehen werden. Darüber hinaus ergab die Vorarbeit des Labors [3], dass verschiedene neuronale Netze, die vollständig auf dieselbe Aufgabe trainiert sind, dazu neigen, ähnliche Interaktionen zu modellieren, sodass wir das Lernen neuronaler Netze als eine Reihe potenzieller Grundwahrheitsinteraktionen betrachten können. Daher kann die Interaktion, die vom neuronalen Netzwerk modelliert wird, wenn es auf Konvergenz trainiert wird, als die Lösung angesehen werden, die man erhält, wenn man die folgende Zielfunktion minimiert:  wobei
wobei  eine Reihe potenzieller Grundwahrheitsinteraktionen darstellt, die das neuronale Netzwerk anpassen muss.
eine Reihe potenzieller Grundwahrheitsinteraktionen darstellt, die das neuronale Netzwerk anpassen muss.  und
und 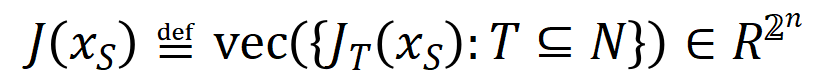 stellen jeweils den Vektor dar, der durch Zusammenfügen aller Gewichte erhalten wird, und den Vektor, der durch Zusammenfügen der Werte aller Interaktionsauslösefunktionen erhalten wird.
stellen jeweils den Vektor dar, der durch Zusammenfügen aller Gewichte erhalten wird, und den Vektor, der durch Zusammenfügen der Werte aller Interaktionsauslösefunktionen erhalten wird. 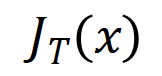
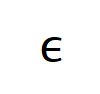 befriedigt
befriedigt 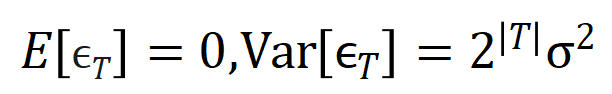 . Und mit fortschreitendem Training wird die Varianz des Rauschens
. Und mit fortschreitendem Training wird die Varianz des Rauschens 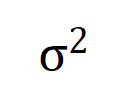 allmählich kleiner.
allmählich kleiner.  kann die analytische Lösung des optimalen Interaktionsgewichts
kann die analytische Lösung des optimalen Interaktionsgewichts  erhalten werden, wie im Satz in der Abbildung unten gezeigt.
erhalten werden, wie im Satz in der Abbildung unten gezeigt. 

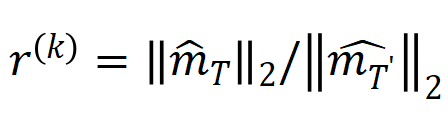 , wobei
, wobei 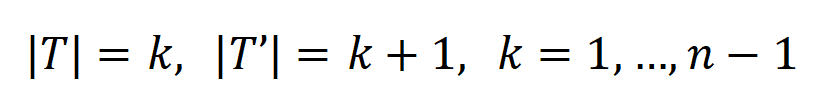 , verwendet werden, um näherungsweise das Verhältnis der Stärke der Wechselwirkung k-ter Ordnung zur Wechselwirkung k+1-ter Ordnung zu messen. In der folgenden Abbildung können wir feststellen, dass bei unterschiedlicher Anzahl von Eingabeeinheiten n und unterschiedlichen Ordnungen k das Verhältnis mit abnehmendem
, verwendet werden, um näherungsweise das Verhältnis der Stärke der Wechselwirkung k-ter Ordnung zur Wechselwirkung k+1-ter Ordnung zu messen. In der folgenden Abbildung können wir feststellen, dass bei unterschiedlicher Anzahl von Eingabeeinheiten n und unterschiedlichen Ordnungen k das Verhältnis mit abnehmendem 
 mit der Verteilung jeder Interaktionsreihenfolge während des tatsächlichen Trainingsprozesses
mit der Verteilung jeder Interaktionsreihenfolge während des tatsächlichen Trainingsprozesses 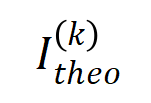 und stellten fest, dass die Theorie: Die Interaktionsverteilung kann die Interaktionsintensitätsverteilung zu jedem Zeitpunkt im tatsächlichen Training gut vorhersagen.
und stellten fest, dass die Theorie: Die Interaktionsverteilung kann die Interaktionsintensitätsverteilung zu jedem Zeitpunkt im tatsächlichen Training gut vorhersagen. 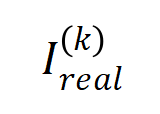

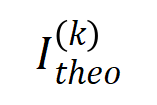 (blaues Histogramm) und der tatsächlichen Interaktionsverteilung
(blaues Histogramm) und der tatsächlichen Interaktionsverteilung 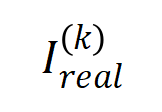 (oranges Histogramm). Die theoretische Interaktionsverteilung sagt die tatsächliche Interaktionsverteilung zu verschiedenen Zeitpunkten in der zweiten Trainingsphase gut voraus und passt sie an. Weitere Ergebnisse finden Sie im Papier.
(oranges Histogramm). Die theoretische Interaktionsverteilung sagt die tatsächliche Interaktionsverteilung zu verschiedenen Zeitpunkten in der zweiten Trainingsphase gut voraus und passt sie an. Weitere Ergebnisse finden Sie im Papier.  erklärt werden kann, wenn der Lärm
erklärt werden kann, wenn der Lärm