Rumah >hujung hadapan web >tutorial js >Pelayaran melalui Algoritma menggunakan Javascript - Bubble Sort
Pelayaran melalui Algoritma menggunakan Javascript - Bubble Sort
- PHPzasal
- 2024-07-29 06:30:53511semak imbas
Apakah Bubble Sort?
Isih Buih ialah salah satu algoritma pengisihan paling mudah dalam sains komputer. Dinamakan untuk cara elemen yang lebih kecil "gelembung" ke bahagian atas senarai dengan setiap lelaran, ia merupakan alat yang sangat baik untuk mengajar asas-asas algoritma pengisihan. Walaupun bukan yang paling cekap untuk set data yang besar, kesederhanaannya menjadikannya titik permulaan yang bagus untuk memahami cara algoritma pengisihan berfungsi.
Cara Isih Buih Berfungsi
Isih Buih berfungsi dengan berulang kali melangkah melalui senarai, membandingkan elemen bersebelahan dan menukarnya jika tertib tersalah. Proses ini diulang sehingga tiada lagi pertukaran diperlukan, menunjukkan bahawa senarai itu diisih.
Berikut ialah pecahan langkah demi langkah:
- Mulakan dengan elemen pertama dalam tatasusunan.
- Bandingkan dengan elemen seterusnya.
- Jika elemen pertama lebih besar daripada elemen kedua, tukar elemen tersebut.
- Beralih ke elemen seterusnya dan ulangi langkah 2-3 sehingga anda sampai ke penghujung tatasusunan.
- Jika sebarang pertukaran telah dibuat, ulangi proses dari awal.
- Jika tiada pertukaran dibuat dalam pas penuh, tatasusunan akan diisih.
Mari kita bayangkan proses ini:
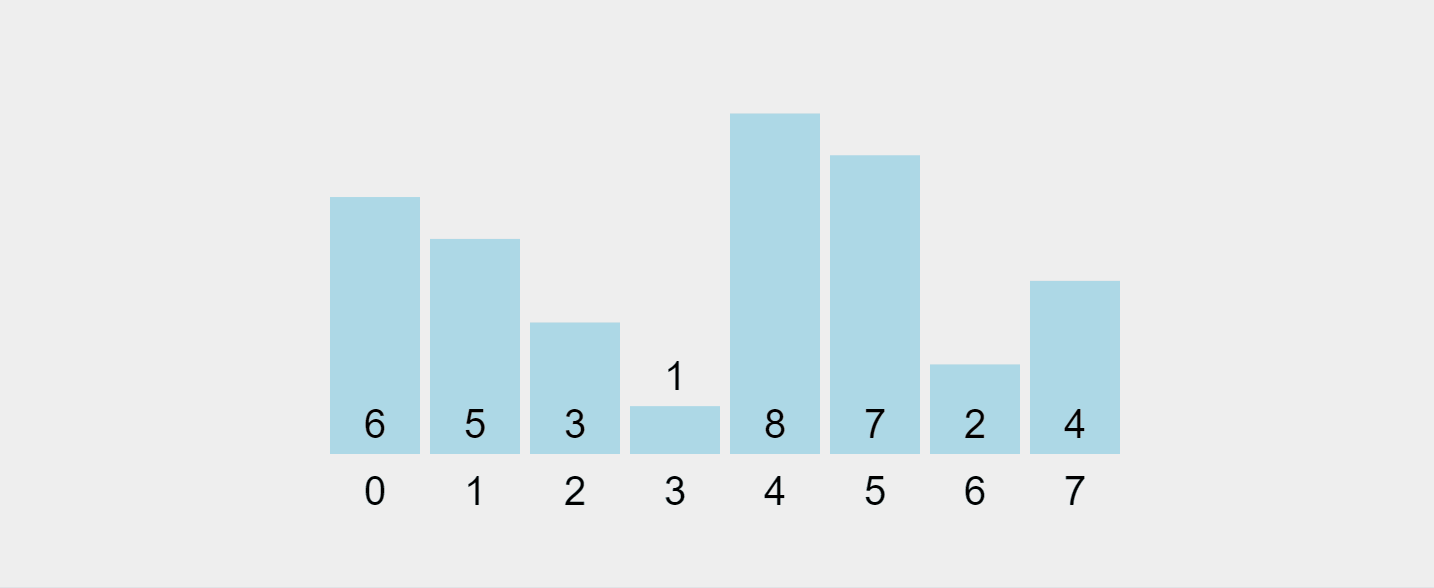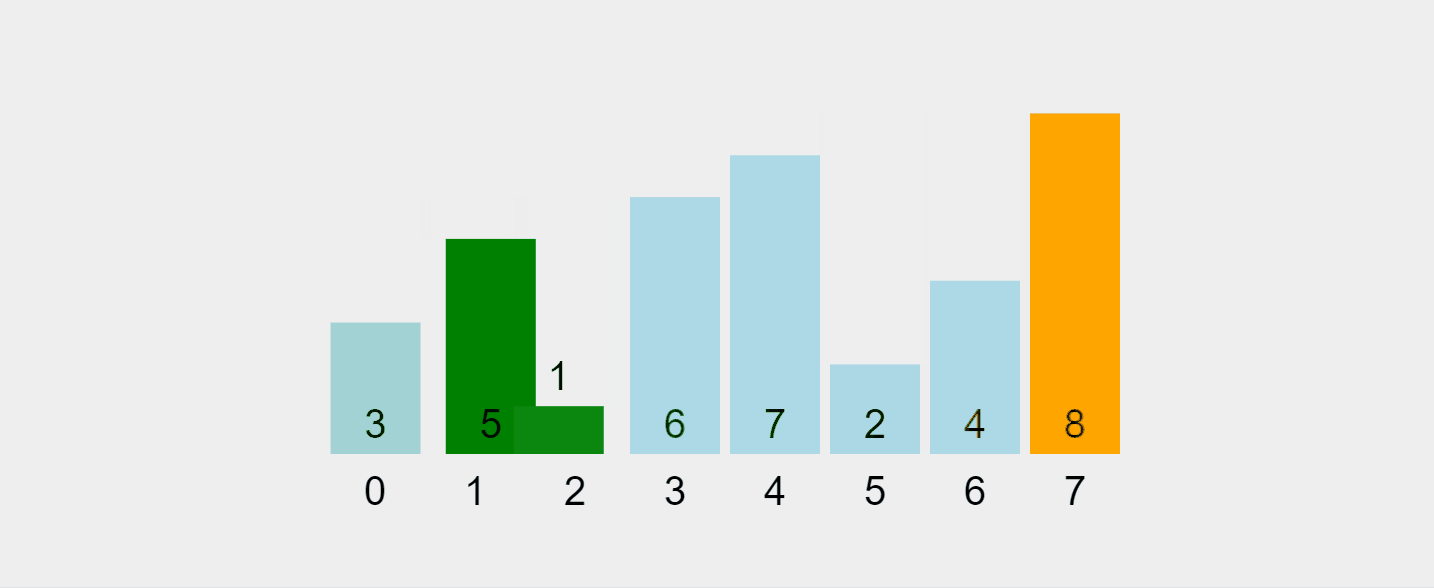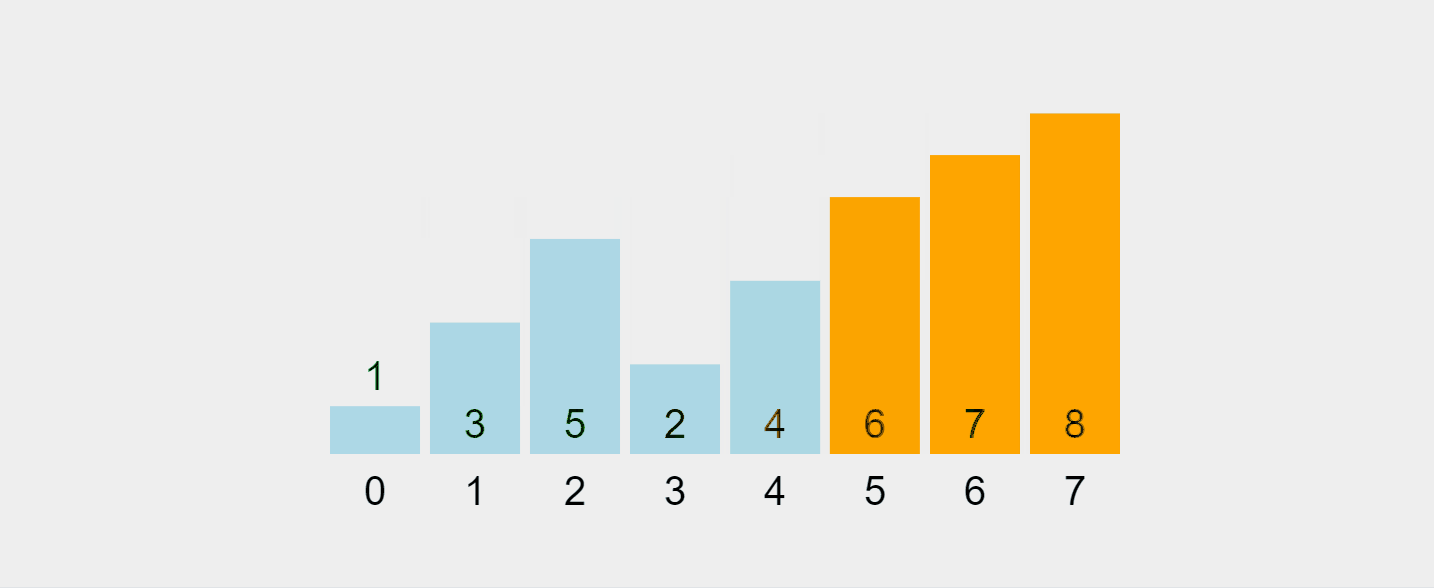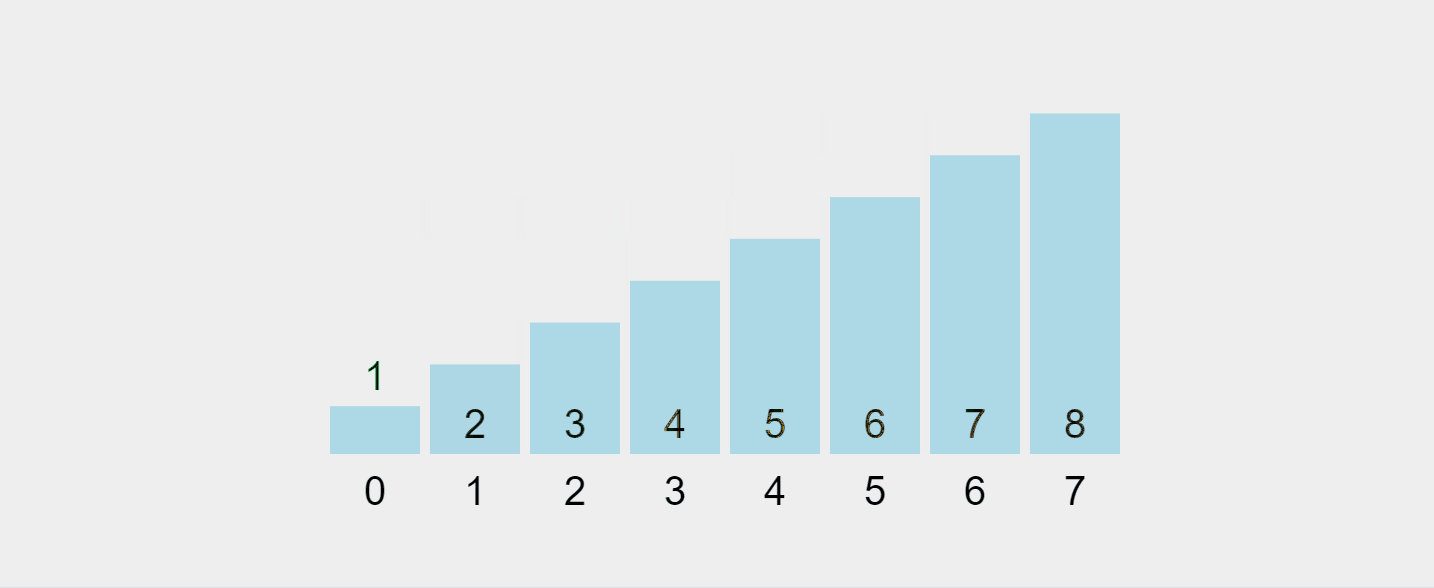
Gif yang dirakam daripada https://visualgo.net/en/sorting
Melaksanakan Bubble Sort dalam JavaScript
Mari kita periksa tiga pelaksanaan Isih Buih dalam JavaScript, setiap satu dengan tahap pengoptimuman yang semakin meningkat.
Pelaksanaan Asas (v1)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Inner loop: compare adjacent elements
for (let j = 0; j < list.length - 1; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
}
}
}
// Return the sorted list
return list;
}
Pelaksanaan asas ini menggunakan gelung bersarang untuk membandingkan dan menukar elemen bersebelahan. Gelung luar memastikan kami membuat hantaran yang mencukupi melalui tatasusunan, manakala gelung dalam melakukan perbandingan dan pertukaran.
Pelaksanaan Dioptimumkan (v2)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Flag to check if any swaps occurred in this pass
let swapped = false;
// Inner loop: compare adjacent elements
for (let j = 0; j < list.length - 1; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
// Set the swapped flag to true
swapped = true;
}
}
// If no swaps occurred in this pass, the list is sorted
if (!swapped) {
break; // Exit the outer loop early
}
}
// Return the sorted list
return list;
}
Versi ini memperkenalkan bendera bertukar untuk menyemak sama ada sebarang pertukaran dibuat dalam pas. Jika tiada pertukaran berlaku, senarai sudah diisih dan kita boleh keluar dari gelung lebih awal.
Pelaksanaan Paling Dioptimumkan (v3)
function bubbleSort(list) {
// Outer loop: iterate through the entire list
for (let i = 0; i < list.length - 1; i++) {
// Flag to check if any swaps occurred in this pass
let swapped = false;
// Inner loop: compare adjacent elements
// Note: We reduce the upper bound by i in each pass
for (let j = 0; j < list.length - 1 - i; j++) {
// If the current element is greater than the next one
if (list[j] > list[j + 1]) {
// Swap the elements using destructuring assignment
[list[j], list[j + 1]] = [list[j + 1], list[j]];
// Set the swapped flag to true
swapped = true;
}
}
// If no swaps occurred in this pass, the list is sorted
if (!swapped) {
break; // Exit the outer loop early
}
}
// Return the sorted list
return list;
}
Pengoptimuman akhir ini mengurangkan julat gelung dalam sebanyak i dalam setiap hantaran. Ini kerana selepas setiap hantaran, elemen terbesar yang tidak diisih "bergelembung" ke kedudukannya yang betul di penghujung tatasusunan.
Analisis Kerumitan Masa dan Ruang
Ciri prestasi Bubble Sort adalah seperti berikut:
-
Kerumitan Masa:
- Kes Terbaik: O(n) - apabila tatasusunan sudah diisih
- Kes Purata: O(n^2)
- Kes Terburuk: O(n^2) - apabila tatasusunan dalam susunan terbalik
Kerumitan Ruang: O(1) - Isih Buih ialah algoritma pengisihan di tempat, hanya memerlukan jumlah memori tambahan yang tetap.
Berbanding dengan algoritma yang lebih maju seperti Isih Pantas (purata O(n log n)) atau Isih Gabung (O(n log n)), kerumitan masa kuadratik Isih Buih menjadikannya tidak cekap untuk set data yang besar.
Kelebihan dan Kelemahan Isih Buih
Kelebihan:
- Mudah untuk difahami dan dilaksanakan
- Isih di tempat (ruang O(1))
- Algoritma pengisihan stabil
- Boleh mengesan senarai yang telah diisih
Kelemahan:
- Tidak cekap untuk set data yang besar (O(n^2))
- Prestasi buruk pada data yang hampir diisih
- Operasi pertukaran yang berlebihan
Bila Menggunakan Bubble Sort
- Tujuan pendidikan: Kesederhanaan menjadikannya sangat baik untuk mengajar konsep algoritma asas.
- Set data kecil: Untuk tatasusunan yang sangat kecil, perbezaan prestasi berbanding dengan algoritma kompleks mungkin boleh diabaikan.
- Data yang hampir diisih: Dengan versi yang dioptimumkan, ia boleh menjadi agak cekap pada senarai yang hampir diisih.
- Persekitaran ingatan terhad: Sifat di tempatnya boleh memberi kelebihan dalam senario yang sangat terhad ingatan.
Isih Koktel: Variasi yang Diperbaiki
Isih Koktel, juga dikenali sebagai Isih Kocok Koktel atau Isih Buih Dwi Arah, ialah versi Isih Buih yang dipertingkat. Ia merentasi senarai dalam kedua-dua arah, membantu mengalihkan elemen ke kedudukan yang betul dengan lebih cekap.
How Cocktail Sort Works
- Start with the first element and move towards the end, swapping adjacent elements if they're in the wrong order.
- When you reach the end, start from the second-to-last element and move towards the beginning, again swapping elements as needed.
- Repeat this process, narrowing the range of elements to check with each pass, until no swaps are needed.
Cocktail Sort is particularly useful in cases where the array has elements that are initially large at the beginning and small at the end, as it can reduce the total number of passes needed compared to traditional Bubble Sort.
Here's a visualization of Cocktail Sort:
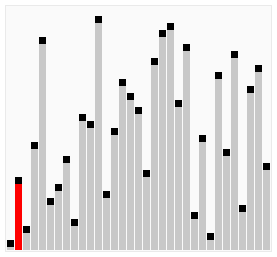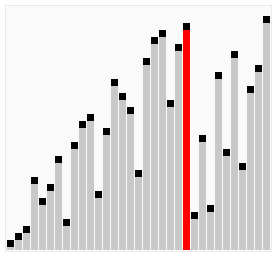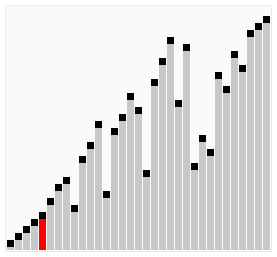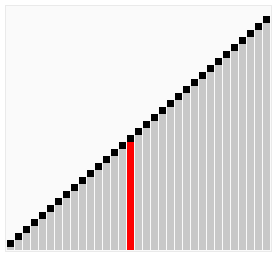
Visual from Wikipedia: https://en.wikipedia.org/wiki/Cocktail_shaker_sort
Cocktail Sort implementation in Javascript
function cocktailSort(list) {
let swapped;
// The do...while loop ensures the sorting continues until no swaps are needed
do {
// Reset the swapped flag at the beginning of each complete iteration
swapped = false;
// First pass: left to right (like standard bubble sort)
for (let i = 0; i < list.length - 1; i++) {
// If the current element is greater than the next, swap them
if (list[i] > list[i + 1]) {
[list[i], list[i + 1]] = [list[i + 1], list[i]];
// Mark that a swap occurred
swapped = true;
}
}
// If no swaps occurred in the first pass, the array is sorted
if (!swapped) {
break; // Exit the do...while loop early
}
// Reset the swapped flag for the second pass
swapped = false;
// Second pass: right to left (this is what makes it "cocktail" sort)
for (let i = list.length - 2; i >= 0; i--) {
// If the current element is greater than the next, swap them
if (list[i] > list[i + 1]) {
[list[i], list[i + 1]] = [list[i + 1], list[i]];
// Mark that a swap occurred
swapped = true;
}
}
// The loop will continue if any swaps occurred in either pass
} while (swapped);
// Return the sorted list
return list;
}
This implementation alternates between forward and backward passes through the list, potentially reducing the number of iterations needed to sort the array.
Practical Applications and Use Cases
While Bubble Sort isn't typically used in production environments for large-scale applications, it can still find use in certain scenarios:
- Educational tools: It's often used to introduce sorting algorithms and algorithm analysis in computer science education.
- Embedded systems: In systems with very limited memory, its in-place sorting can be advantageous.
- Small datasets: For sorting small lists (e.g., less than 50 elements), its simplicity might outweigh the performance benefits of more complex algorithms.
- Nearly sorted data: If data is known to be almost sorted, an optimized Bubble Sort can be reasonably efficient.
- Sorting stability requirement: When a stable sort is needed and simplicity is preferred over efficiency, Bubble Sort can be a straightforward choice.
Conclusion
Bubble Sort, despite its inefficiencies with large datasets, offers valuable insights into the world of sorting algorithms and algorithm analysis. Its straightforward approach makes it an excellent teaching tool for beginners in computer science.
Key takeaways are:
- It's simple to understand and implement.
- It has a time complexity of O(n^2), making it inefficient for large datasets.
- It's an in-place and stable sorting algorithm.
- Optimizations can improve its performance, especially for nearly sorted data.
- It's primarily used for educational purposes and in scenarios with very small datasets or limited memory.
While you're unlikely to use Bubble Sort in production code for large-scale applications, the principles behind it are fundamental to many algorithms. The process of optimizing Bubble Sort teaches valuable lessons about algorithm improvement, serving as a stepping stone to more advanced computational problem-solving.
When it comes to algorithms, there's rarely a one-size-fits-all solution. The best algorithm for a given task depends on the specific requirements, constraints, and characteristics of your data. Bubble Sort, with all its limitations, still has its place in this diverse algorithmic ecosystem.
Atas ialah kandungan terperinci Pelayaran melalui Algoritma menggunakan Javascript - Bubble Sort. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Artikel berkaitan
Lihat lagi- Analisis mendalam bagi komponen kumpulan senarai Bootstrap
- Penjelasan terperinci tentang fungsi JavaScript kari
- Contoh lengkap penjanaan kata laluan JS dan pengesanan kekuatan (dengan muat turun kod sumber demo)
- Angularjs menyepadukan UI WeChat (weui)
- Cara cepat bertukar antara Cina Tradisional dan Cina Ringkas dengan JavaScript dan helah untuk tapak web menyokong pertukaran antara kemahiran_javascript Cina Ringkas dan Tradisional

