CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!

GEMM(일반 행렬 곱셈)은 많은 응용 프로그램과 알고리즘의 중요한 부분이며 컴퓨터 하드웨어 성능을 평가하는 중요한 지표 중 하나이기도 합니다. GEMM 구현에 대한 심층적인 연구와 최적화는 고성능 컴퓨팅과 소프트웨어와 하드웨어 시스템 간의 관계를 더 잘 이해하는 데 도움이 될 수 있습니다. 컴퓨터 과학에서 GEMM의 효과적인 최적화는 컴퓨팅 속도를 높이고 리소스를 절약할 수 있으며, 이는 컴퓨터 시스템의 전반적인 성능을 향상시키는 데 중요합니다. GEMM의 작동 원리와 최적화 방법에 대한 심층적인 이해는 현대 컴퓨팅 하드웨어의 잠재력을 더 잘 활용하고 다양하고 복잡한 컴퓨팅 작업에 대한 보다 효율적인 솔루션을 제공하는 데 도움이 될 것입니다. GEMM의 성능을 최적화하고 개선함으로써 다음을 추가할 수 있습니다.

1. GEMM의 기본 특성

1.1 GEMM 계산 프로세스 및 복잡성

GEMM은 다음과 같이 정의됩니다.

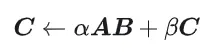
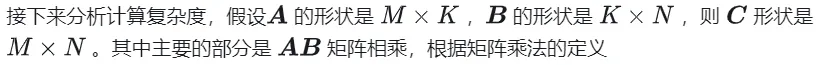
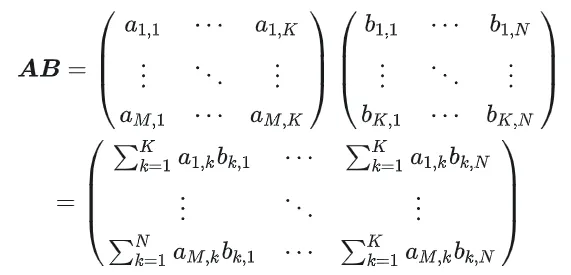
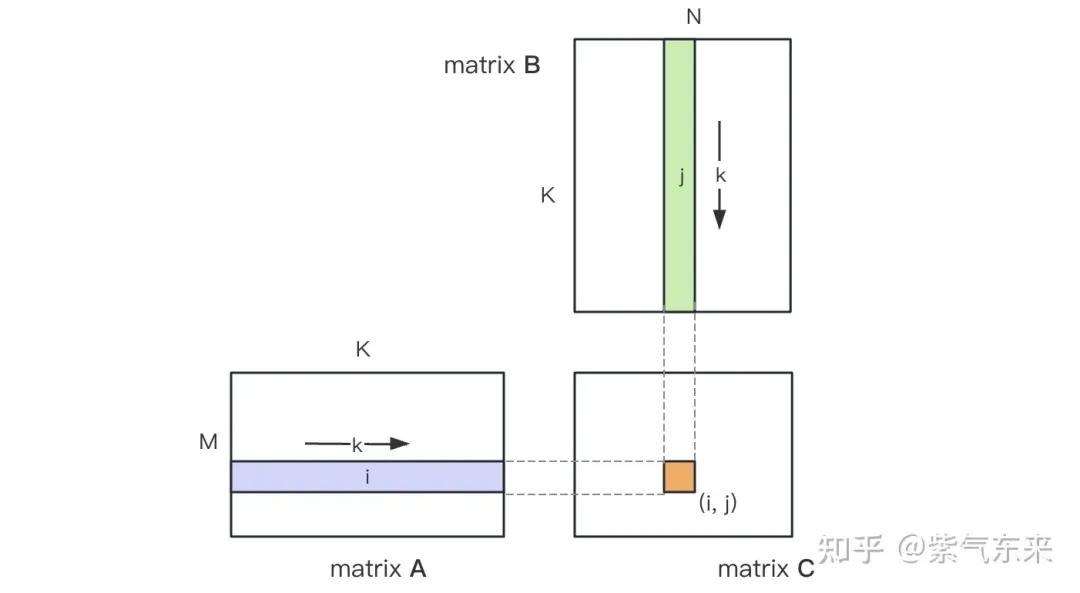
행렬 곱셈의 계산 다이어그램

1.2 간단한 구현 및 프로세스 분석

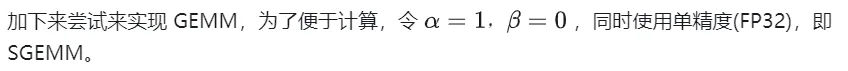
다음은 원래 정의에 따라 CPU에 구현된 코드이며 컨트롤로 사용됩니다. 정확성을 위해

#define OFFSET(row, col, ld) ((row) * (ld) + (col))void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K) {for (int m = 0; m 

다음은 CUDA를 사용하여 가장 간단한 행렬 곱셈인 Kernal을 구현합니다. 전체 행렬 곱셈을 완료하는 데 총 M * N 스레드가 사용됩니다. 각 스레드는 행렬 C의 요소 계산을 담당하며 K번의 곱셈과 누산을 완료해야 합니다. 행렬 A, B 및 C는 모두 전역 메모리에 저장됩니다(수정자 __global__ 에 의해 결정됨). 전체 코드는 sgemm_naive.cu를 참조하세요.

__global__ void naiveSgemm(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {int n = blockIdx.x * blockDim.x + threadIdx.x;int m = blockIdx.y * blockDim.y + threadIdx.y;if (m 

컴파일이 완료되었으며 Tesla V100-PCIE-32GB에서 실행한 결과는 다음과 같습니다. V100 백서에 따르면 FP32의 최대 컴퓨팅 파워는 15.7 TFLOPS이므로 이의 컴퓨팅 파워 활용도는 다음과 같습니다. 방법은 11.5%에 불과하다.

rreee

다음은 위 계산 프로세스의 워크플로를 자세히 분석하기 위한 예로 M=512, K=512, N=512를 사용합니다.

1. 전역 메모리에서 행렬 A, B, C에 각각 저장 공간을 할당합니다.
2. 행렬 때문에 C의 각 요소 계산은 서로 독립적이므로 병렬성 매핑에서 각 스레드는 행렬 C의 1 요소 계산에 해당합니다.
3. 실행 구성의 GridSize와 blockSize는 모두 x를 갖습니다. (열 방향) , y (행 방향) 2차원, 그중

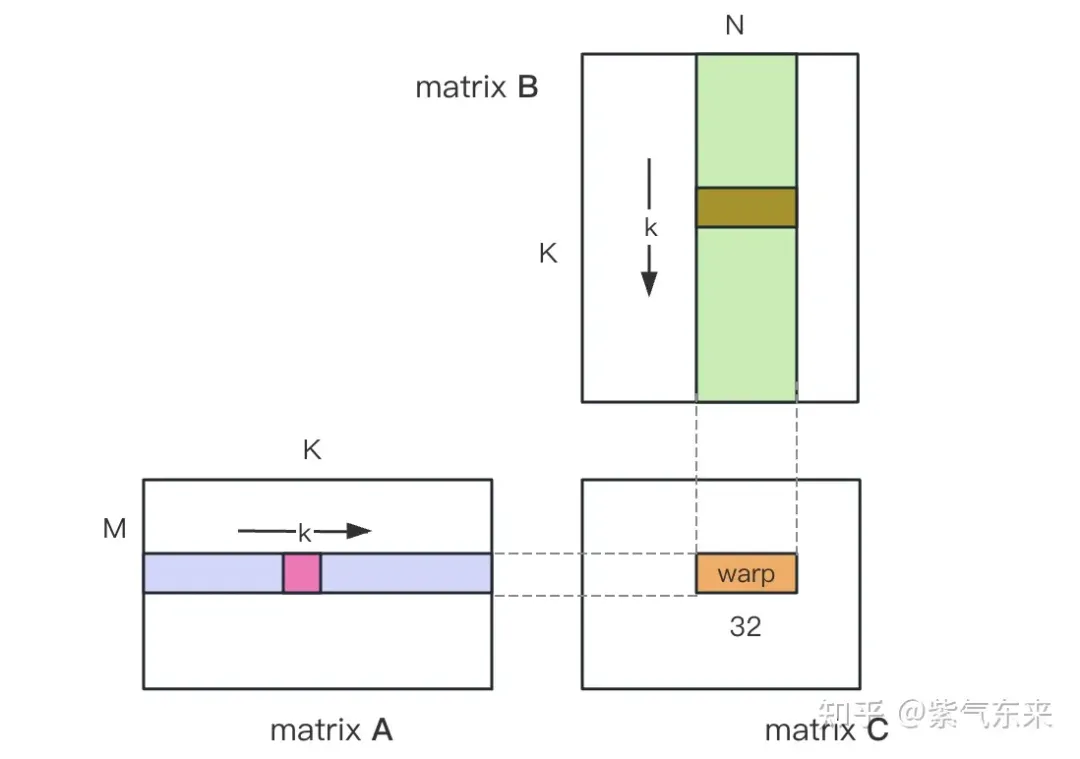
nsys는 순진한 프로파일링 버전을 기록합니다

2. GEMM 최적화 탐색

이전 기사에서는 단지 기능적인 GEMM만 구현했지만 성능은 기대와는 거리가 멀습니다. 이 섹션에서는 주로 GEMM 성능 최적화에 대해 연구합니다.

2.1 공유 메모리를 사용한 행렬 분할

위 계산에서는 곱셈 및 누산 작업을 완료하기 위해 두 개의 전역 메모리 로드가 필요합니다. 계산 메모리 액세스 비율이 매우 낮으며 효과적인 데이터 재사용이 없습니다. 따라서 공유 메모리를 사용하면 반복되는 메모리 읽기를 줄일 수 있습니다.

먼저 행렬 C를 BMxBN 크기의 동일한 블록으로 나눕니다. 각 블록은 블록으로 계산되며, 여기서 각 스레드는 행렬 C의 TMxTN 요소를 계산합니다. 그 후, 계산에 필요한 모든 데이터는 smem에서 읽혀지며, 이는 A 및 B 행렬의 반복적인 메모리 읽기의 일부를 제거합니다. 공유 메모리의 용량이 제한되어 있다는 점을 고려하면 BK 크기의 블록은 매번 K 차원으로 읽을 수 있습니다. 이러한 루프는 전체 행렬 곱셈 연산을 완료하는 데 총 K/BK 시간이 필요하며 블록의 결과를 얻을 수 있습니다. 프로세스는 아래 그림에 나와 있습니다.

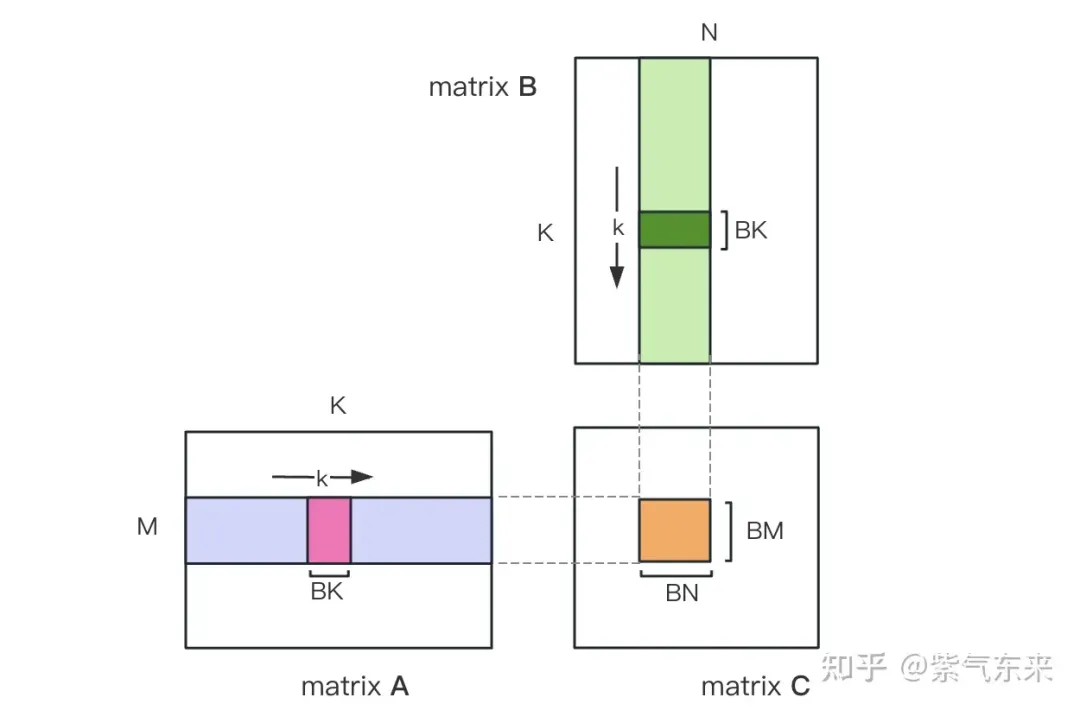
공유 메모리를 사용한 최적화 후 각 블록에 대해 다음을 얻을 수 있습니다.

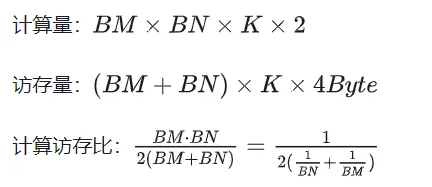
위 공식에서 BM과 BN이 클수록 계산 메모리 액세스 비율이 높을수록 성능이 향상됩니다. 그러나 공유 메모리 용량 제한(V100 1 SM은 96KB에 불과)으로 인해 블록은 BK * (BM + BN) * 4바이트를 차지해야 합니다.

TM과 TN의 값도 두 가지 측면에서 제한됩니다. 한편으로는 블록에 BM/TM *BN/TN 스레드가 있습니다. 1024를 초과하고 SM에 영향을 미치지 않도록 너무 높을 수는 없습니다. 반면에, 레지스터 수에는 제한이 있습니다. 스레드는 부분 합계를 저장하기 위해 최소한 TM * TN 레지스터가 필요합니다. 모든 레지스터 수는 256개를 초과할 수 없으며 동시에 SM의 병렬 스레드 수에 영향을 주지 않도록 너무 높을 수 없습니다.

마지막으로 BM = BN = 128, BK = 8, TM = TN = 8을 선택하면 계산된 메모리 액세스 비율은 32입니다. V100 15.7TFLOPS의 이론적 컴퓨팅 성능에 따르면 15.7TFLOPS/32 = 490GB/s를 얻을 수 있습니다. 측정된 HBM 대역폭은 763GB/s에 따르면 이 시점에서는 대역폭이 더 이상 컴퓨팅 성능을 제한하지 않는다는 것을 알 수 있습니다. 시간.

위 분석을 바탕으로 커널 함수 구현 프로세스는 다음과 같습니다. 전체 코드는 sgemm_v1.cu를 참조하세요. 주요 단계는 다음과 같습니다.

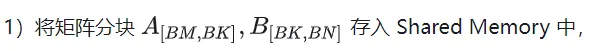
A B 행렬 분할의 스레드 인덱스 관계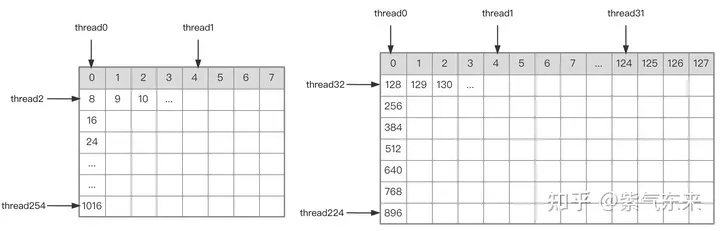

确定好单个block的执行过程，接下来需要确定多block处理的不同分块在Global Memory中的对应关系，仍然以A为例进行说明。由于分块沿着行的方向移动，那么首先需要确定行号，根据 Grid 的二维全局线性索引关系，by * BM 表示该分块的起始行号，同时我们已知load_a_smem_m 为分块内部的行号，因此全局的行号为load_a_gmem_m = by * BM + load_a_smem_m 。由于分块沿着行的方向移动，因此列是变化的，需要在循环内部计算，同样也是先计算起始列号bk * BK 加速分块内部列号load_a_smem_k 得到 load_a_gmem_k = bk * BK + load_a_smem_k ，由此我们便可以确定了分块在原始数据中的位置OFFSET(load_a_gmem_m, load_a_gmem_k, K) 。同理可分析矩阵分块 的情况，不再赘述。

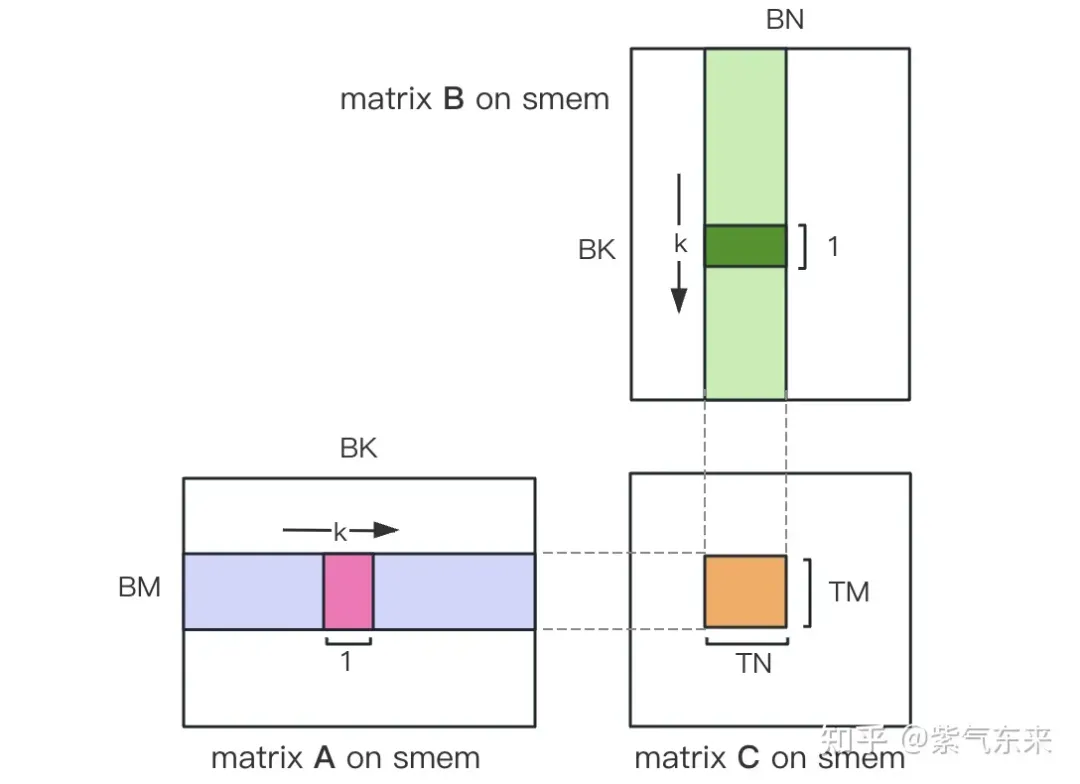
计算完后，还需要将其存入 Global Memory 中，这就需要计算其在 Global Memory 中的对应关系。由于存在更小的分块，则行和列均由3部分构成：全局行号store_c_gmem_m 等于大分块的起始行号by * BM+小分块的起始行号ty * TM+小分块内部的相对行号 i 。列同理。

__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {const int BM = 128;const int BN = 128;const int BK = 8;const int TM = 8;const int TN = 8;const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = ty * blockDim.x + tx;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;// tid/2, row of s_aint load_a_smem_k = (tid & 1) > 5; // tid/32, row of s_bint load_b_smem_n = (tid & 31) 

计算结果如下，性能达到了理论峰值性能的51.7%：

M N K =128128 1024, Time = 0.00031578 0.00031727 0.00032288 s, AVG Performance =98.4974 GflopsM N K =192192 1024, Time = 0.00031638 0.00031720 0.00031754 s, AVG Performance = 221.6661 GflopsM N K =256256 1024, Time = 0.00031488 0.00031532 0.00031606 s, AVG Performance = 396.4287 GflopsM N K =384384 1024, Time = 0.00031686 0.00031814 0.00032080 s, AVG Performance = 884.0425 GflopsM N K =512512 1024, Time = 0.00031814 0.00032007 0.00032493 s, AVG Performance =1562.1563 GflopsM N K =768768 1024, Time = 0.00032397 0.00034419 0.00034848 s, AVG Performance =3268.5245 GflopsM N K = 1024 1024 1024, Time = 0.00034570 0.00034792 0.00035331 s, AVG Performance =5748.3952 GflopsM N K = 1536 1536 1024, Time = 0.00068797 0.00068983 0.00069094 s, AVG Performance =6523.3424 GflopsM N K = 2048 2048 1024, Time = 0.00136173 0.00136552 0.00136899 s, AVG Performance =5858.5604 GflopsM N K = 3072 3072 1024, Time = 0.00271910 0.00273115 0.00274006 s, AVG Performance =6590.6331 GflopsM N K = 4096 4096 1024, Time = 0.00443805 0.00445964 0.00446883 s, AVG Performance =7175.4698 GflopsM N K = 6144 6144 1024, Time = 0.00917891 0.00950608 0.00996963 s, AVG Performance =7574.0999 GflopsM N K = 8192 8192 1024, Time = 0.01628838 0.01645271 0.01660790 s, AVG Performance =7779.8733 GflopsM N K =1228812288 1024, Time = 0.03592557 0.03597434 0.03614323 s, AVG Performance =8005.7066 GflopsM N K =1638416384 1024, Time = 0.06304122 0.06306373 0.06309302 s, AVG Performance =8118.7715 Gflops

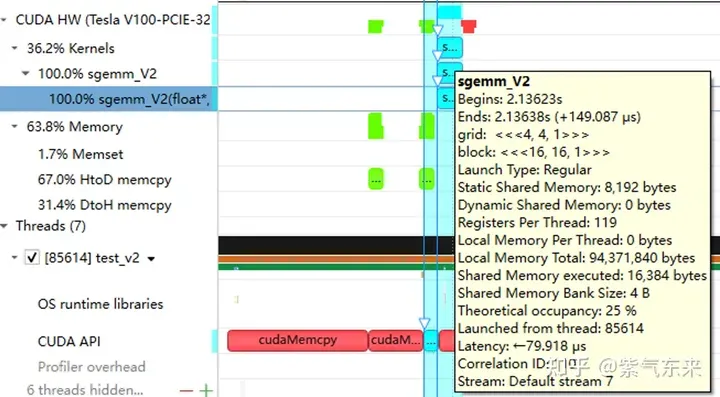
下面仍以M=512,K=512,N=512为例，分析一下结果。首先通过 profiling 可以看到 Shared Memory 占用为 8192 bytes，这与理论上(128+128)X8X4完全一致。

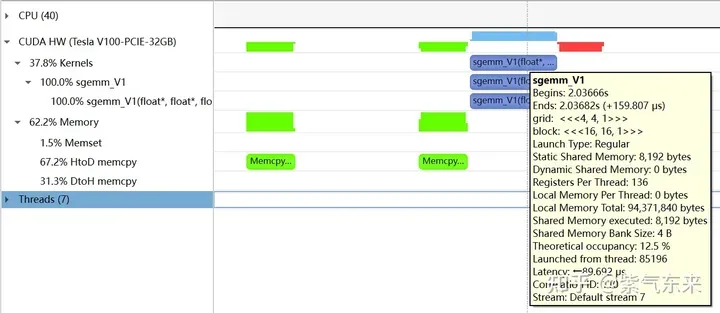nsys 记录 的 V1 版本的 profiling

profiling 显示 Occupancy 为 12.5%，可以通过 cuda-calculator 加以印证，该例中 threads per block = 256, Registers per thread = 136, 由此可以计算得到每个SM中活跃的 warp 为8，而对于V100，每个SM中的 warp 总数为64，因此 Occupancy 为 8/64 = 12.5%。

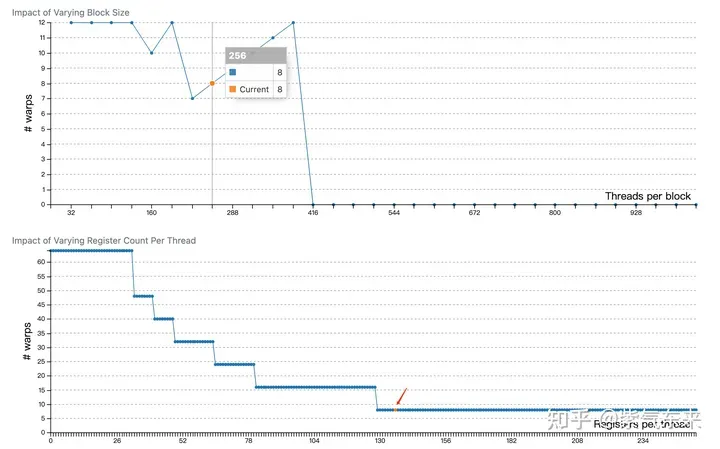
2.2 解决 Bank Conflict 问题

上节通过利用 Shared Memory 大幅提高了访存效率，进而提高了性能，本节将进一步优化 Shared Memory 的使用。

Shared Memory一共划分为32个Bank，每个Bank的宽度为4 Bytes，如果需要访问同一个Bank的多个数据，就会发生Bank Conflict。例如一个Warp的32个线程，如果访问的地址分别为0、4、8、...、124，就不会发生Bank Conflict，只占用Shared Memory一拍的时间；如果访问的地址为0、8、16、...、248，这样一来地址0和地址128对应的数据位于同一Bank、地址4和地址132对应的数据位于同一Bank，以此类推，那么就需要占用Shared Memory两拍的时间才能读出。

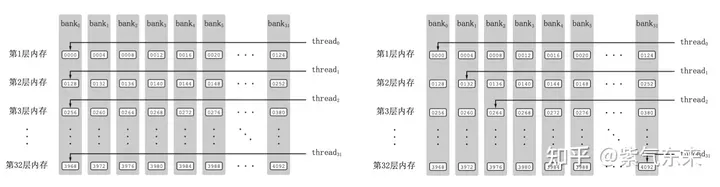
有 Bank Conflict VS 无 Bank Conflict

再看 V1 版本计算部分的三层循环，每次从Shared memory中取矩阵A的长度为TM的向量和矩阵B的长度为TN的向量，这两个向量做外积并累加到部分和中，一次外积共TM * TN次乘累加，一共需要循环BK次取数和外积。

接下来分析从Shared Memory load的过程中存在的Bank Conflict：

i) 取矩阵A需要取一个列向量，而矩阵A在Shared Memory中是按行存储的；

ii) 在TM = TN = 8的情况下，无论矩阵A还是矩阵B，从Shared Memory中取数时需要取连续的8个数，即便用LDS.128指令一条指令取四个数，也需要两条指令，由于一个线程的两条load指令的地址是连续的，那么同一个Warp不同线程的同一条load指令的访存地址就是被间隔开的，便存在着 Bank Conflict。

为了解决上述的两点Shared Memory的Bank Conflict，采用了一下两点优化：

i) 为矩阵A分配Shared Memory时形状分配为[BK][BM]，即让矩阵A在Shared Memory中按列存储

ii) 将原本每个线程负责计算的TM * TN的矩阵C，划分为下图中这样的两块TM/2 * TN的矩阵C，由于TM/2=4，一条指令即可完成A的一块的load操作，两个load可同时进行。

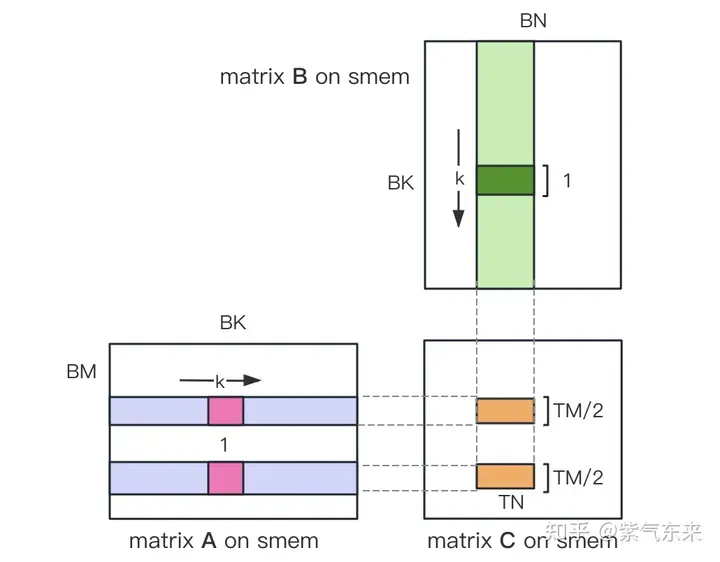
kernel 函数的核心部分实现如下，完整代码见 sgemm_v2.cu 。

__shared__ float s_a[BK][BM];__shared__ float s_b[BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

结果如下，相对未解决 Bank Conflict 版(V1) 性能提高了 14.4%，达到了理论峰值的74.3%。

M N K =128128 1024, Time = 0.00029699 0.00029918 0.00030989 s, AVG Performance = 104.4530 GflopsM N K =192192 1024, Time = 0.00029776 0.00029828 0.00029882 s, AVG Performance = 235.7252 GflopsM N K =256256 1024, Time = 0.00029485 0.00029530 0.00029619 s, AVG Performance = 423.2949 GflopsM N K =384384 1024, Time = 0.00029734 0.00029848 0.00030090 s, AVG Performance = 942.2843 GflopsM N K =512512 1024, Time = 0.00029853 0.00029945 0.00030070 s, AVG Performance =1669.7479 GflopsM N K =768768 1024, Time = 0.00030458 0.00032467 0.00032790 s, AVG Performance =3465.1038 GflopsM N K = 1024 1024 1024, Time = 0.00032406 0.00032494 0.00032621 s, AVG Performance =6155.0281 GflopsM N K = 1536 1536 1024, Time = 0.00047990 0.00048224 0.00048461 s, AVG Performance =9331.3912 GflopsM N K = 2048 2048 1024, Time = 0.00094426 0.00094636 0.00094992 s, AVG Performance =8453.4569 GflopsM N K = 3072 3072 1024, Time = 0.00187866 0.00188096 0.00188538 s, AVG Performance =9569.5816 GflopsM N K = 4096 4096 1024, Time = 0.00312589 0.00319050 0.00328147 s, AVG Performance = 10029.7885 GflopsM N K = 6144 6144 1024, Time = 0.00641280 0.00658940 0.00703498 s, AVG Performance = 10926.6372 GflopsM N K = 8192 8192 1024, Time = 0.01101130 0.01116194 0.01122950 s, AVG Performance = 11467.5446 GflopsM N K =1228812288 1024, Time = 0.02464854 0.02466705 0.02469344 s, AVG Performance = 11675.4946 GflopsM N K =1638416384 1024, Time = 0.04385955 0.04387468 0.04388355 s, AVG Performance = 11669.5995 Gflops

分析一下 profiling 可以看到 Static Shared Memory 仍然是使用了8192 Bytes，奇怪的的是，Shared Memory executed 却翻倍变成了 16384 Bytes（知友如果知道原因可以告诉我一下）。

2.3 流水并行化：Double Buffering

Double Buffering，即双缓冲，即通过增加buffer的方式，使得 访存-计算 的串行模式流水线化，以减少等待时间，提高计算效率，其原理如下图所示:

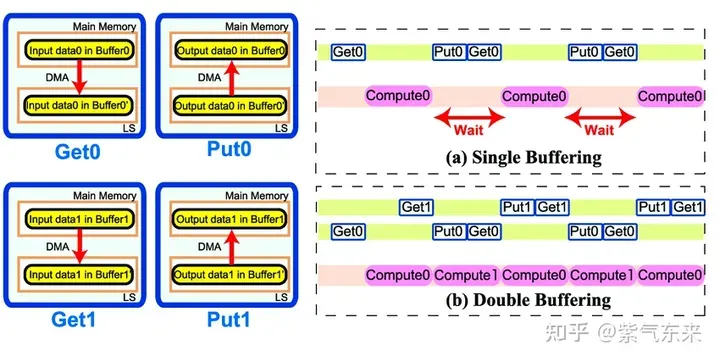
Single Buffering VS Double Buffering

具体到 GEMM 任务中来，就是需要两倍的Shared Memory，之前只需要BK * (BM + BN) * 4 Bytes的Shared Memory，采用Double Buffering之后需要2BK * (BM + BN) * 4 Bytes的Shared Memory，然后使其 pipeline 流动起来。

代码核心部分如下所示，完整代码参见 sgemm_v3.cu 。有以下几点需要注意：

1）主循环从bk = 1 开始，第一次数据加载在主循环之前，最后一次计算在主循环之后，这是pipeline 的特点决定的；

2）由于计算和下一次访存使用的Shared Memory不同，因此主循环中每次循环只需要一次__syncthreads()即可

3）由于GPU不能向CPU那样支持乱序执行，主循环中需要先将下一次循环计算需要的Gloabal Memory中的数据load 到寄存器，然后进行本次计算，之后再将load到寄存器中的数据写到Shared Memory，这样在LDG指令向Global Memory做load时，不会影响后续FFMA及其它运算指令的 launch 执行，也就达到了Double Buffering的目的。

__shared__ float s_a[2][BK][BM];__shared__ float s_b[2][BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

性能如下所示，达到了理论峰值的 80.6%。

M N K =128128 1024, Time = 0.00024000 0.00024240 0.00025792 s, AVG Performance = 128.9191 GflopsM N K =192192 1024, Time = 0.00024000 0.00024048 0.00024125 s, AVG Performance = 292.3840 GflopsM N K =256256 1024, Time = 0.00024029 0.00024114 0.00024272 s, AVG Performance = 518.3728 GflopsM N K =384384 1024, Time = 0.00024070 0.00024145 0.00024198 s, AVG Performance =1164.8394 GflopsM N K =512512 1024, Time = 0.00024173 0.00024237 0.00024477 s, AVG Performance =2062.9786 GflopsM N K =768768 1024, Time = 0.00024291 0.00024540 0.00026010 s, AVG Performance =4584.3820 GflopsM N K = 1024 1024 1024, Time = 0.00024534 0.00024631 0.00024941 s, AVG Performance =8119.7302 GflopsM N K = 1536 1536 1024, Time = 0.00045712 0.00045780 0.00045872 s, AVG Performance =9829.5167 GflopsM N K = 2048 2048 1024, Time = 0.00089632 0.00089970 0.00090656 s, AVG Performance =8891.8924 GflopsM N K = 3072 3072 1024, Time = 0.00177891 0.00178289 0.00178592 s, AVG Performance = 10095.9883 GflopsM N K = 4096 4096 1024, Time = 0.00309763 0.00310057 0.00310451 s, AVG Performance = 10320.6843 GflopsM N K = 6144 6144 1024, Time = 0.00604826 0.00619887 0.00663078 s, AVG Performance = 11615.0253 GflopsM N K = 8192 8192 1024, Time = 0.01031738 0.01045051 0.01048861 s, AVG Performance = 12248.2036 GflopsM N K =1228812288 1024, Time = 0.02283978 0.02285837 0.02298272 s, AVG Performance = 12599.3212 GflopsM N K =1638416384 1024, Time = 0.04043287 0.04044823 0.04046151 s, AVG Performance = 12658.1556 Gflops

从 profiling 可以看到双倍的 Shared Memory 的占用

三、cuBLAS 实现方式探究

本节我们将认识CUDA的标准库——cuBLAS， 即NVIDIA版本的基本线性代数子程序 (Basic Linear Algebra Subprograms, BLAS) 规范实现代码。它支持 Level 1 (向量与向量运算) ，Level 2 (向量与矩阵运算) ，Level 3 (矩阵与矩阵运算) 级别的标准矩阵运算。

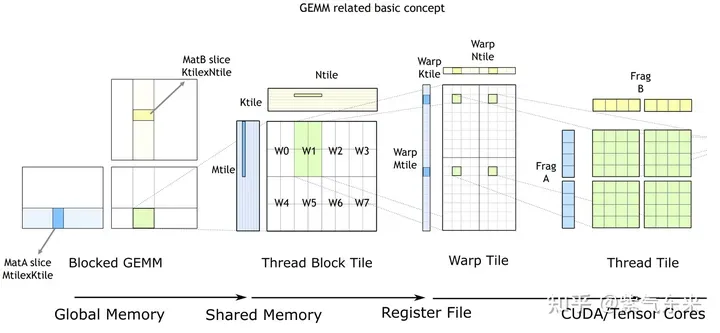
cuBLAS/CUTLASS GEMM的基本过程

如上图所示，计算过程分解成线程块片（thread block tile）、线程束片（warp tile）和线程片（thread tile）的层次结构并将AMP的策略应用于此层次结构来高效率的完成基于GPU的拆分成tile的GEMM。这个层次结构紧密地反映了NVIDIA CUDA编程模型。可以看到从global memory到shared memory的数据移动（矩阵到thread block tile）；从shared memory到寄存器的数据移动（thread block tile到warp tile）；从寄存器到CUDA core的计算（warp tile到thread tile）。

cuBLAS 实现了单精度矩阵乘的函数cublasSgemm，其主要参数如下：

cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 cublasOperation_t transa, // A 矩阵是否需要转置 cublasOperation_t transb, // B 矩阵是否需要转置 int m, // A 的行数 int n, // B 的列数 int k, // A 的列数 const float *alpha, // 系数 α, host or device pointer const float *A, // 矩阵 A 的指针，device pointer int lda, // 矩阵 A 的主维，if A 转置， lda = max(1, k), else max(1, m) const float *B, // 矩阵 B 的指针, device pointer int ldb, // 矩阵 B 的主维，if B 转置， ldb = max(1, n), else max(1, k) const float *beta, // 系数 β, host or device pointer float *C, // 矩阵 C 的指针，device pointer int ldc // 矩阵 C 的主维，ldc >= max(1, m) );

调用方式如下：

cublasHandle_t cublas_handle;cublasCreate(&cublas_handle);float cublas_alpha = 1.0;float cublas_beta = 0;cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);

性能如下所示，达到了理论峰值的 82.4%。

M N K =128128 1024, Time = 0.00002704 0.00003634 0.00010822 s, AVG Performance = 860.0286 GflopsM N K =192192 1024, Time = 0.00003155 0.00003773 0.00007267 s, AVG Performance =1863.6689 GflopsM N K =256256 1024, Time = 0.00003917 0.00004524 0.00007747 s, AVG Performance =2762.9438 GflopsM N K =384384 1024, Time = 0.00005318 0.00005978 0.00009120 s, AVG Performance =4705.0655 GflopsM N K =512512 1024, Time = 0.00008326 0.00010280 0.00013840 s, AVG Performance =4863.9646 GflopsM N K =768768 1024, Time = 0.00014278 0.00014867 0.00018816 s, AVG Performance =7567.1560 GflopsM N K = 1024 1024 1024, Time = 0.00023485 0.00024460 0.00028150 s, AVG Performance =8176.5614 GflopsM N K = 1536 1536 1024, Time = 0.00046474 0.00047607 0.00051181 s, AVG Performance =9452.3201 GflopsM N K = 2048 2048 1024, Time = 0.00077930 0.00087862 0.00092307 s, AVG Performance =9105.2126 GflopsM N K = 3072 3072 1024, Time = 0.00167904 0.00168434 0.00171114 s, AVG Performance = 10686.6837 GflopsM N K = 4096 4096 1024, Time = 0.00289619 0.00291068 0.00295904 s, AVG Performance = 10994.0128 GflopsM N K = 6144 6144 1024, Time = 0.00591766 0.00594586 0.00596915 s, AVG Performance = 12109.2611 GflopsM N K = 8192 8192 1024, Time = 0.01002384 0.01017465 0.01028435 s, AVG Performance = 12580.2896 GflopsM N K =1228812288 1024, Time = 0.02231159 0.02233805 0.02245619 s, AVG Performance = 12892.7969 GflopsM N K =1638416384 1024, Time = 0.03954650 0.03959291 0.03967242 s, AVG Performance = 12931.6086 Gflops

由此可以对比以上各种方法的性能情况，可见手动实现的性能已接近于官方的性能，如下：

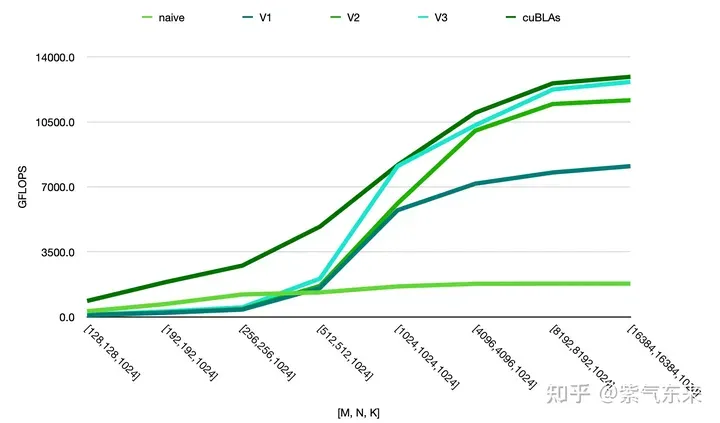
위 내용은 CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!