KMGP(Kernel Model Gaussian Processes)를 사용한 데이터 모델링

KMGP(Kernel Model Gaussian Processes)는 다양한 데이터 세트의 복잡성을 처리하기 위한 정교한 도구입니다. 커널 기능을 통해 전통적인 가우스 프로세스의 개념을 확장합니다. 이 기사에서는 KMGP의 이론적 기초, 실제 적용 및 과제에 대해 자세히 논의합니다.

커널 모델 가우시안 프로세스는 기존 가우시안 프로세스의 확장이며 기계 학습 및 통계에 사용됩니다. kmgp를 이해하기 전에 가우시안 프로세스에 대한 기본 지식을 숙지하고 커널 모델의 역할을 이해해야 합니다.

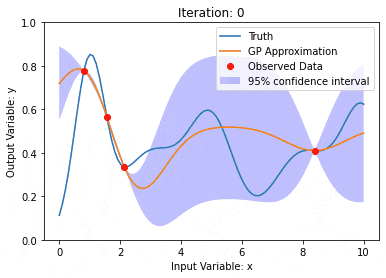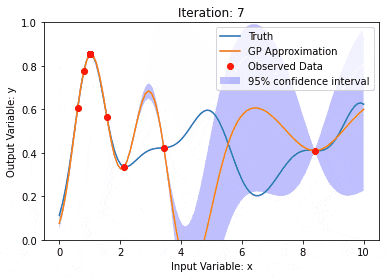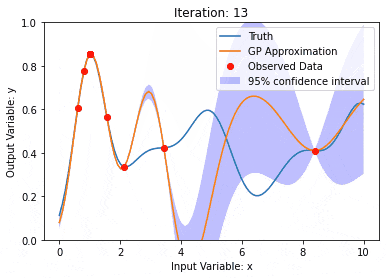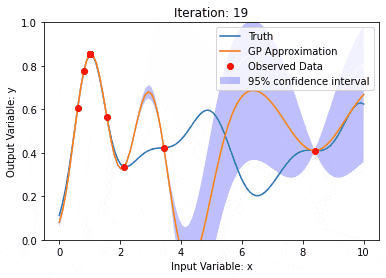
Gaussian process(GP)

Gaussian process는 함수 확률 분포를 정의하는 데 사용되는 제한된 수의 변수가 Gaussian에 의해 공동으로 배포되는 확률 변수 세트입니다.

가우스 프로세스는 기계 학습의 회귀 및 분류 작업에 일반적으로 사용되며 데이터의 확률 분포를 맞추는 데 사용할 수 있습니다.

가우스 프로세스의 중요한 특징은 불확실성 추정 및 예측을 제공하는 기능입니다. 이는 예측 자체만큼 중요한 예측의 신뢰도를 이해하는 작업에 매우 유용합니다.

커널 함수 모델링

가우스 프로세스에서 커널 함수(또는 공분산 함수)는 서로 다른 데이터 포인트 간의 유사성을 측정하는 데 사용됩니다. 커널 함수는 두 개의 입력을 받아 이들 사이의 유사성 점수를 계산합니다.

선형, 다항식, 방사형 기저 함수(RBF) 등 다양한 유형의 커널이 있습니다. 각 코어는 서로 다른 특성을 갖고 있으며, 문제에 따라 적절한 코어를 선택할 수 있습니다.

가우스 프로세스에서 커널 모델링은 데이터의 기본 패턴을 가장 잘 포착하기 위해 커널 기능을 선택하고 최적화하는 프로세스입니다. 커널의 선택과 구성이 가우스 프로세스의 성능에 큰 영향을 미칠 수 있기 때문에 이 단계는 매우 중요합니다.

커널 모델 가우시안 프로세스(KMGP)

KMGP는 표준 GP(가우시안 프로세스)의 확장으로, 커널 기능 적용에 중점을 둡니다. 표준 GP와 비교하여 KMGP는 특정 유형의 데이터 또는 문제에 따라 복잡하거나 맞춤 설계된 커널 기능을 사용자 정의하는 데 더 많은 관심을 기울입니다. 이 접근 방식은 데이터가 복잡하고 표준 커널 기능이 기본 관계를 캡처하지 못할 때 특히 유용합니다. 그러나 KMGP에서 커널 기능을 설계하고 조정하는 것은 어렵고 문제 영역 및 통계 모델링에 대한 깊은 영역 지식과 전문적인 경험이 필요한 경우가 많습니다.

커널 모델 가우시안 프로세스는 복잡한 데이터 세트를 모델링하는 유연하고 강력한 방법을 제공하는 정교한 통계 학습 도구입니다. 불확실성 추정치를 제공하는 능력과 맞춤형 조정을 통해 다양한 유형의 데이터를 조정하는 적응성으로 인해 특히 높이 평가됩니다.

KMGP에서 잘 설계된 커널은 데이터의 비선형 추세, 주기성 및 이분산성(다양한 노이즈 수준)과 같은 복잡한 현상을 모델링할 수 있습니다. 따라서 심층적인 도메인 지식과 통계 모델링에 대한 철저한 이해가 필요합니다.

KMGP는 다양한 분야에 적용할 수 있습니다. 지리통계학에서는 기본 지리적 변화를 포착하기 위해 공간 데이터를 모델링합니다. 금융에서는 주가를 예측하는 데 사용되며 금융 시장의 불안정하고 복잡한 특성을 설명합니다. 로봇 공학 및 제어 시스템에서 KMGP는 불확실성이 있는 동적 시스템의 동작을 모델링하고 예측합니다.

코드

합성 데이터 세트를 사용하여 완전한 Python 코드 예제를 생성합니다. 여기서는 가우시안 프로세스 처리를 전문으로 하는 Python 라이브러리인 GPy 라이브러리를 사용합니다.

pip install numpy matplotlib GPy

라이브러리 가져오기

import numpy as np import matplotlib.pyplot as plt import GPy

그런 다음 numpy를 사용하여 합성 데이터 세트를 생성합니다.

X = np.linspace(0, 10, 100)[:, None] Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)

GPy를 사용하여 가우스 프로세스 모델을 정의하고 학습합니다.

kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.) model = GPy.models.GPRegression(X, Y, kernel) model.optimize(messages=True)

모델을 학습한 후 이를 사용하여 테스트 데이터세트에 대한 예측을 수행합니다. 그런 다음 그래프를 그려 모델 성능을 시각화합니다.

X_test = np.linspace(-2, 12, 200)[:, None] Y_pred, Y_var = model.predict(X_test)  plt.figure(figsize=(10, 5)) plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction') plt.fill_between(X_test.flatten(), (Y_pred - 2*np.sqrt(Y_var)).flatten(), (Y_pred + 2*np.sqrt(Y_var)).flatten(), alpha=0.5, color='pink', label='Confidence Interval') plt.scatter(X, Y, c='b', label='Training Data') plt.xlabel('X') plt.ylabel('Y') plt.title('Kernel Modeled Gaussian Process Regression') plt.legend() plt.show()

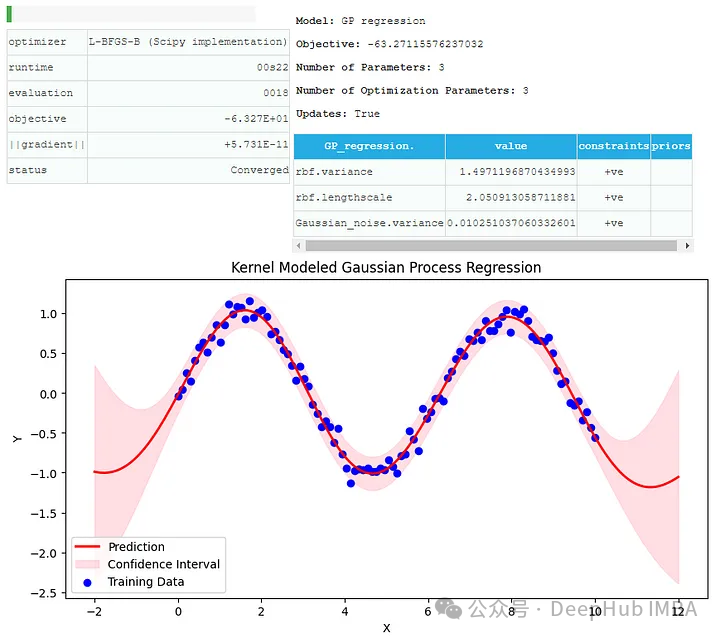
여기서 RBF 커널을 사용하여 가우시안 프로세스 회귀 모델을 적용하면 예측 및 훈련 데이터와 신뢰 구간을 볼 수 있습니다.

요약

커널 모델 가우시안 프로세스는 통계 학습 분야의 주요 발전을 나타내며 복잡한 데이터 세트를 이해하기 위한 유연하고 강력한 프레임워크를 제공합니다. GPy에는 기본적으로 우리가 볼 수 있는 모든 커널 기능이 포함되어 있습니다. 다음은 공식 문서의 스크린샷입니다.

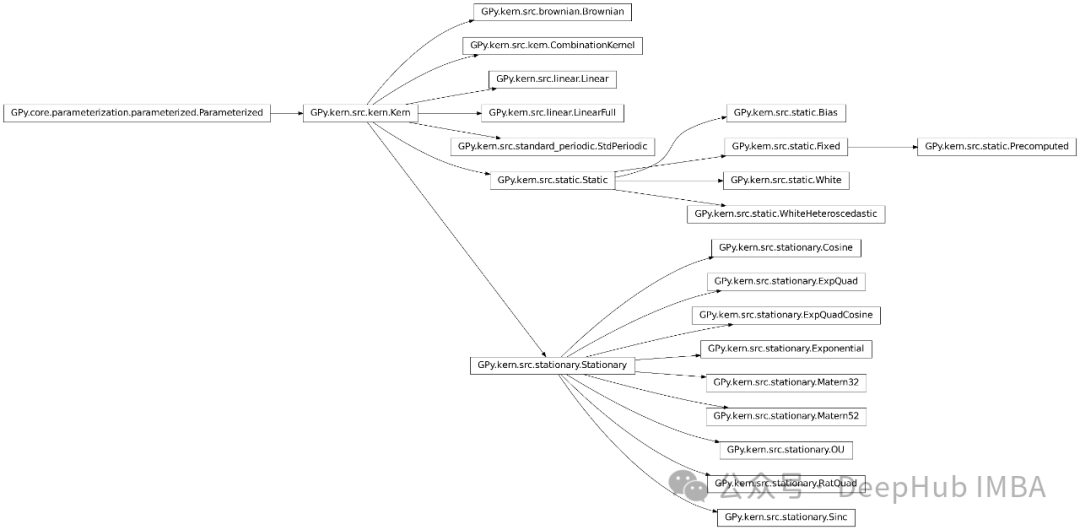
다음은 공식 GPy A 흐름입니다. 차트가 제공됩니다

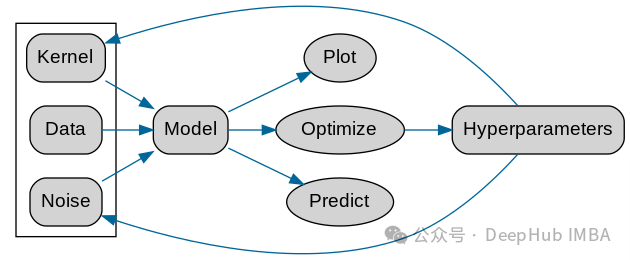
위 내용은 KMGP(Kernel Model Gaussian Processes)를 사용한 데이터 모델링의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!