
MCMC-EM 알고리즘이라고도 불리는 Markov Chain Monte Carlo EM 알고리즘은 비지도 학습에서 매개변수 추정에 사용되는 통계 알고리즘입니다. 핵심 아이디어는 숨은 변수가 있는 확률 모델의 매개변수 추정을 위해 마르코프 체인 몬테 카를로 방법과 기대 최대화 알고리즘을 결합하는 것입니다. 반복을 통해 MCMC-EM 알고리즘은 점차적으로 매개변수의 최대 우도 추정에 접근할 수 있습니다. 효율적이고 유연하며 다양한 분야에서 널리 사용됩니다.
MCMC-EM 알고리즘의 기본 아이디어는 MCMC 방법을 사용하여 숨겨진 변수의 샘플을 얻고, 이 샘플을 사용하여 기대값을 계산한 다음 EM 알고리즘을 사용하여 로그 우도 함수를 최대화하는 것입니다. . 이 알고리즘의 반복 프로세스에는 MCMC 샘플링과 EM 업데이트의 두 단계가 포함됩니다. MCMC 샘플링 단계에서는 MCMC 방법을 사용하여 잠재 변수의 사후 분포를 추정하고, EM 업데이트 단계에서는 EM 알고리즘을 사용하여 모델 매개변수를 추정합니다. 이 두 단계를 번갈아 수행함으로써 모델의 매개변수 추정치를 지속적으로 최적화할 수 있습니다. 정리하면, MCMC-EM 알고리즘은 MCMC와 EM을 결합하여 모델 매개변수와 잠재변수의 사후 분포를 추정하는 반복 알고리즘이다.
1.MCMC Sampling
MCMC 샘플링 단계에서는 먼저 초기 상태를 선택하고 마르코프 체인의 전이 확률을 통해 샘플 시퀀스를 생성해야 합니다. 마르코프 체인은 상태 시퀀스이며, 각 상태는 이전 상태에만 관련되어 있으므로 시퀀스가 커짐에 따라 현재 상태의 확률 분포는 안정적인 분포를 보이는 경향이 있습니다. 생성된 샘플 시퀀스가 안정적인 분포를 가지도록 하려면 MCMC 샘플링에 적절한 전이 확률을 사용해야 합니다. 일반적인 MCMC 방법에는 Metropolis-Hastings 알고리즘과 Gibbs 샘플링 알고리즘이 포함됩니다. 이러한 방법은 다양한 전이 확률을 통해 표본 생성 및 분포 근사치를 달성하여 목표 분포의 샘플링을 얻습니다. Metropolis-Hastings 알고리즘은 수락-거부 메커니즘을 사용하여 전송 수락 여부를 결정하는 반면 Gibbs 샘플링 알고리즘은 조건부 분포를 사용하여 전송을 수행합니다. 이러한 방법은 통계 및 기계 학습에 널리 사용되며 복잡한 샘플링 및 추론 문제를 해결할 수 있습니다.
2.EM update
EM 업데이트 단계에서는 MCMC 샘플링으로 얻은 샘플을 사용하여 잠재변수의 기대값을 추정해야 하며, 이러한 기대값은 잠재변수의 최대화에 사용됩니다. 로그 우도 함수. EM 알고리즘은 반복 알고리즘이며 각 반복에는 E 단계와 M 단계의 두 단계가 포함됩니다. E 단계에서는 잠재변수의 사후분포를 계산하고 잠재변수의 기대값을 계산하는 작업이 필요하다. M 단계에서는 E 단계에서 계산된 숨은 변수의 기대값을 사용하여 매개변수의 최대 우도 추정값을 풀기 위해 로그 우도 함수를 최대화해야 합니다.
MCMC-EM 알고리즘의 장점은 복잡한 확률 모델을 더 잘 처리할 수 있고 샘플링 방법을 통해 더 많은 샘플을 생성하여 모델 매개변수를 더 잘 추정할 수 있다는 것입니다. 또한 MCMC-EM 알고리즘은 MCMC 방법의 매개변수를 조정하여 샘플링 효율성과 샘플링 정확도의 균형을 유지함으로써 알고리즘의 성능을 향상시킬 수 있습니다.
그러나 MCMC-EM 알고리즘에도 몇 가지 문제와 과제가 있습니다. 첫째, MCMC-EM 알고리즘은 특히 대용량 데이터를 처리할 때 많은 컴퓨팅 자원과 시간을 필요로 한다. 둘째, MCMC-EM 알고리즘은 천천히 수렴하는 경향이 있으며 수렴을 달성하려면 많은 반복이 필요합니다. 마지막으로 MCMC-EM 알고리즘의 결과는 MCMC 방법 선택 및 매개변수 설정에 따라 영향을 받을 수 있으므로 적절한 디버깅 및 최적화가 필요합니다.
일반적으로 MCMC-EM 알고리즘은 중요한 비지도 학습 알고리즘으로 확률 모델의 매개변수 추정, 밀도 추정 등의 분야에서 널리 사용됩니다. MCMC-EM 알고리즘에는 몇 가지 문제와 과제가 있지만 컴퓨팅 자원의 지속적인 개선과 알고리즘 최적화를 통해 MCMC-EM 알고리즘은 더욱 실용적이고 효과적이 될 것입니다.
위 내용은 몬테카를로 마르코프 체인 EM 알고리즘의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
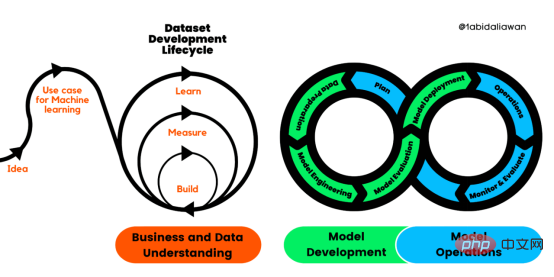 解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM
解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM译者 | 布加迪审校 | 孙淑娟目前,没有用于构建和管理机器学习(ML)应用程序的标准实践。机器学习项目组织得不好,缺乏可重复性,而且从长远来看容易彻底失败。因此,我们需要一套流程来帮助自己在整个机器学习生命周期中保持质量、可持续性、稳健性和成本管理。图1. 机器学习开发生命周期流程使用质量保证方法开发机器学习应用程序的跨行业标准流程(CRISP-ML(Q))是CRISP-DM的升级版,以确保机器学习产品的质量。CRISP-ML(Q)有六个单独的阶段:1. 业务和数据理解2. 数据准备3. 模型
 2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM
2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM机器学习是一个不断发展的学科,一直在创造新的想法和技术。本文罗列了2023年机器学习的十大概念和技术。 本文罗列了2023年机器学习的十大概念和技术。2023年机器学习的十大概念和技术是一个教计算机从数据中学习的过程,无需明确的编程。机器学习是一个不断发展的学科,一直在创造新的想法和技术。为了保持领先,数据科学家应该关注其中一些网站,以跟上最新的发展。这将有助于了解机器学习中的技术如何在实践中使用,并为自己的业务或工作领域中的可能应用提供想法。2023年机器学习的十大概念和技术:1. 深度神经网
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
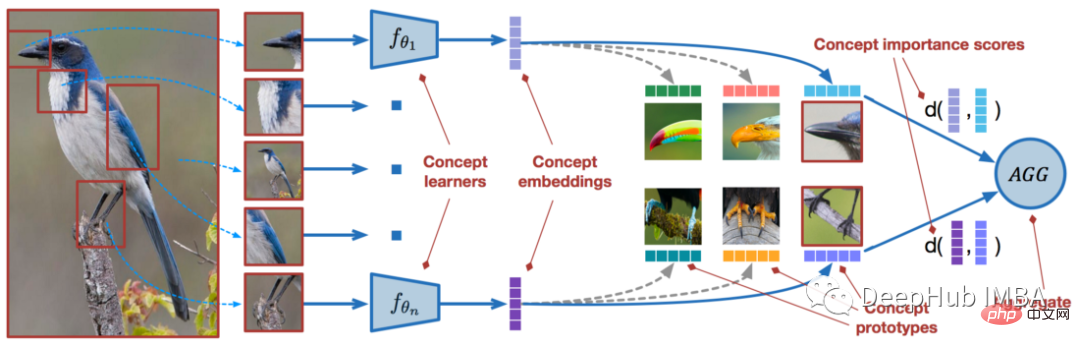 使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM
使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM近年来,基于深度学习的模型在目标检测和图像识别等任务中表现出色。像ImageNet这样具有挑战性的图像分类数据集,包含1000种不同的对象分类,现在一些模型已经超过了人类水平上。但是这些模型依赖于监督训练流程,标记训练数据的可用性对它们有重大影响,并且模型能够检测到的类别也仅限于它们接受训练的类。由于在训练过程中没有足够的标记图像用于所有类,这些模型在现实环境中可能不太有用。并且我们希望的模型能够识别它在训练期间没有见到过的类,因为几乎不可能在所有潜在对象的图像上进行训练。我们将从几个样本中学习
 LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM
LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。 摘要本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。本文包括的内容如下:简介LazyPredict模块的安装在分类模型中实施LazyPredict
 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
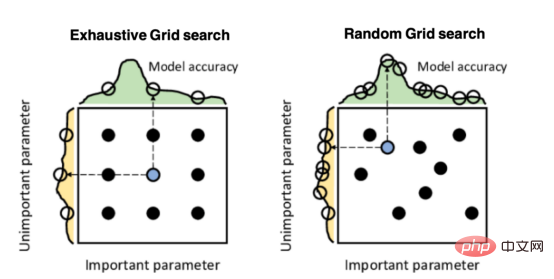
 超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM
超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM本文将详细介绍用来提高机器学习效果的最常见的超参数优化方法。 译者 | 朱先忠审校 | 孙淑娟简介通常,在尝试改进机器学习模型时,人们首先想到的解决方案是添加更多的训练数据。额外的数据通常是有帮助(在某些情况下除外)的,但生成高质量的数据可能非常昂贵。通过使用现有数据获得最佳模型性能,超参数优化可以节省我们的时间和资源。顾名思义,超参数优化是为机器学习模型确定最佳超参数组合以满足优化函数(即,给定研究中的数据集,最大化模型的性能)的过程。换句话说,每个模型都会提供多个有关选项的调整“按钮
 人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM
人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM实现自我完善的过程是“机器学习”。机器学习是人工智能核心,是使计算机具有智能的根本途径;它使计算机能模拟人的学习行为,自动地通过学习来获取知识和技能,不断改善性能,实现自我完善。机器学习主要研究三方面问题:1、学习机理,人类获取知识、技能和抽象概念的天赋能力;2、学习方法,对生物学习机理进行简化的基础上,用计算的方法进行再现;3、学习系统,能够在一定程度上实现机器学习的系统。


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

SublimeText3 Linux 새 버전
SublimeText3 Linux 최신 버전

PhpStorm 맥 버전
최신(2018.2.1) 전문 PHP 통합 개발 도구

Atom Editor Mac 버전 다운로드
가장 인기 있는 오픈 소스 편집기

Eclipse용 SAP NetWeaver 서버 어댑터
Eclipse를 SAP NetWeaver 애플리케이션 서버와 통합합니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

뜨거운 주제
 1371
1371 52
52 39
39 19
19


