
몬테카를로 시뮬레이션 방법은 무작위 샘플링을 기반으로 한 시뮬레이션 방법으로, 복잡한 시스템이나 프로세스를 시뮬레이션하고 확률 분포나 특성을 얻는 데 사용됩니다. 머신러닝 분야에서는 몬테카를로 시뮬레이션 방법이 컴퓨터 비전, 자연어 처리, 강화학습 등의 문제에 널리 사용됩니다. 이 기사에서는 몇 가지 일반적인 몬테카를로 시뮬레이션 방법 모델과 알고리즘을 소개합니다.
Markov Chain Monte Carlo (MCMC)
Markov Chain Monte Carlo는 Markov Chain을 기반으로 한 Monte Carlo 시뮬레이션 방법으로, 복잡한 확률 분포를 계산하는 데 사용됩니다. MCMC 알고리즘에서는 상태 전이가 마르코프 체인의 속성을 충족하는지 확인하기 위해 상태 전이 확률 행렬을 정의해야 합니다. 그런 다음 이 상태 전이 확률 행렬을 사용하여 샘플을 생성하고 이 샘플을 사용하여 확률 분포를 추정할 수 있습니다.
MCMC 알고리즘 중 가장 일반적으로 사용되는 것은 Metropolis-Hastings 알고리즘입니다. 알고리즘은 제안 분포를 정의하여 새 샘플을 생성하고 수락 확률을 사용하여 새 샘플을 수락할지 여부를 결정합니다. 구체적으로, 합격 확률은 새 샘플의 확률 분포 값을 기존 샘플의 확률 분포 값으로 나눈 값과 제안된 분포 값을 곱한 값과 같습니다. 합격 확률이 1보다 크거나 같으면 새 샘플을 수락하고, 그렇지 않으면 합격 확률을 확률로 사용하여 새 샘플을 수락합니다. 이러한 방식으로 지속적으로 새로운 샘플을 생성하고 수락함으로써 MCMC 알고리즘은 목표 분포로 수렴할 수 있으며 복잡한 확률 분포를 시뮬레이션하고 추정하는 데 사용될 수 있습니다.
중요도 샘플링
중요도 샘플링은 복소 적분이나 기대값을 계산하는 데 자주 사용되는 샘플링 기반 몬테카를로 시뮬레이션 방법입니다. 중요도 샘플링 알고리즘에서는 샘플에 가중치를 부여하는 중요도 함수를 정의해야 합니다. 이 중요도 함수를 사용하면 샘플을 생성하고 이러한 샘플을 사용하여 기대치 또는 적분을 추정할 수 있습니다. 중요도 샘플링 모델 및 알고리즘은 샘플링 기반 중요도 샘플링과 중요도 함수 기반 중요도 샘플링 방법의 두 가지 유형으로 나눌 수 있습니다. 샘플링 기반 중요도 샘플링에서는 중요도 함수에서 샘플을 추출하고 이 샘플을 사용하여 기대치 또는 적분을 계산합니다. 중요도 함수 기반 중요도 샘플링에서는 기대값이나 적분값을 계산하기 위해 중요도 함수의 형태를 직접 사용합니다. 두 방법 모두 장점과 단점이 있습니다. 특정 문제의 특성에 따라 적절한 방법을 선택하면 계산 효율성과 정확성을 높일 수 있습니다.
샘플링 기반 중요도 샘플링 알고리즘에서는 단순 분포에서 샘플을 추출한 다음 중요도 함수를 사용하여 이러한 샘플에 가중치를 부여합니다. 구체적으로 목표 분포와 단순 분포를 정의한 다음 단순 분포에서 표본을 추출하고 목표 분포에 대한 각 표본의 가중치를 계산합니다. 마지막으로 이러한 샘플의 가중치를 사용하여 기대치 또는 적분을 추정합니다.
중요도 함수 기반 중요도 샘플링 알고리즘에서는 샘플에 가중치를 부여하는 중요도 함수를 정의합니다. 구체적으로, 목표 분포와 중요도 함수를 정의한 다음, 목표 분포에서 표본을 추출하고 중요도 함수를 사용하여 이러한 표본에 가중치를 부여합니다. 마지막으로 이러한 가중 샘플을 사용하여 기대치 또는 적분을 추정합니다.
Monte Carlo Tree Search (MCTS)
Monte Carlo Tree Search는 복잡한 의사결정 문제를 해결하는 데 자주 사용되는 몬테카를로 시뮬레이션 기반의 강화학습 알고리즘입니다. MCTS 알고리즘에서는 Monte Carlo 시뮬레이션을 사용하여 각 결정의 값을 추정하고 이 값을 사용하여 검색 트리를 업데이트합니다. 구체적으로, 우리는 현재 상태에서 시작하여 Monte Carlo 시뮬레이션을 사용하여 일부 샘플을 생성하고 이러한 샘플을 사용하여 각 결정의 가치를 추정합니다. 그런 다음 이 값을 사용하여 검색 트리를 업데이트하고 최적의 결정을 선택합니다.
확률적 경사 해밀턴-몬테 카를로(SGHMC)
확률적 경사 해밀턴-몬테 카를로는 일반적으로 대규모 데이터 세트에서 베이지안 신경망을 훈련하는 데 사용됩니다. SGHMC 알고리즘에서는 해밀턴 동역학을 사용하여 시스템 동작을 시뮬레이션하고 확률적 경사하강법을 사용하여 매개변수를 업데이트합니다. 구체적으로, 우리는 시스템의 에너지를 설명하기 위해 해밀턴 함수를 정의한 다음 해밀턴 동역학을 사용하여 시스템의 동작을 시뮬레이션합니다. 동시에 확률론적 경사하강법을 사용하여 매개변수를 업데이트하고 확률적 경사도를 사용하여 각 샘플의 경사도를 추정합니다. 마지막으로 이러한 샘플을 사용하여 모델의 매개변수 분포를 추정합니다.
간단히 말하면 몬테카를로 시뮬레이션 방법은 기계 학습에 널리 사용되며 많은 복잡한 문제를 해결하는 데 도움이 될 수 있습니다. 이러한 방법에는 서로 다른 모델과 알고리즘이 있지만 핵심 아이디어는 확률 분포, 기대값 또는 적분을 추정하기 위한 무작위 샘플링을 기반으로 합니다. 기계 학습 기술이 계속 발전함에 따라 몬테카를로 시뮬레이션 방법은 더 복잡한 문제를 해결하는 데 계속해서 중요한 역할을 할 것입니다.
위 내용은 몬테카를로 시뮬레이션을 위한 공통 모델 및 알고리즘의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 신속한 엔지니어링에서 생각의 그래프는 무엇입니까?Apr 13, 2025 am 11:53 AM
신속한 엔지니어링에서 생각의 그래프는 무엇입니까?Apr 13, 2025 am 11:53 AM소개 신속한 엔지니어링에서 "Thought of Thought"는 그래프 이론을 사용하여 AI의 추론 과정을 구성하고 안내하는 새로운 접근법을 나타냅니다. 종종 선형 S와 관련된 전통적인 방법과 달리
 Genai 에이전트와 함께 조직의 이메일 마케팅을 최적화하십시오Apr 13, 2025 am 11:44 AM
Genai 에이전트와 함께 조직의 이메일 마케팅을 최적화하십시오Apr 13, 2025 am 11:44 AM소개 축하해요! 당신은 성공적인 사업을 운영합니다. 웹 페이지, 소셜 미디어 캠페인, 웹 세미나, 컨퍼런스, 무료 리소스 및 기타 소스를 통해 매일 5000 개의 이메일 ID를 수집합니다. 다음 명백한 단계는입니다
 Apache Pinot을 사용한 실시간 앱 성능 모니터링Apr 13, 2025 am 11:40 AM
Apache Pinot을 사용한 실시간 앱 성능 모니터링Apr 13, 2025 am 11:40 AM소개 오늘날의 빠르게 진행되는 소프트웨어 개발 환경에서 최적의 애플리케이션 성능이 중요합니다. 응답 시간, 오류율 및 자원 활용과 같은 실시간 메트릭 모니터링 메인이 도움이 될 수 있습니다.
 Chatgpt가 10 억 명의 사용자를 쳤습니까? Openai CEO는'몇 주 만에 두 배가되었습니다Apr 13, 2025 am 11:23 AM
Chatgpt가 10 억 명의 사용자를 쳤습니까? Openai CEO는'몇 주 만에 두 배가되었습니다Apr 13, 2025 am 11:23 AM"얼마나 많은 사용자가 있습니까?" 그는 자극했다. Altman은“마지막으로 우리가 마지막으로 말한 것은 매주 5 억 명의 행위자이며 매우 빠르게 성장하고 있다고 생각합니다. 앤더슨은 계속해서“당신은 나에게 몇 주 만에 두 배가되었다고 말했습니다. “저는 그 개인이라고 말했습니다
 Pixtral -12B : Mistral AI의 첫 번째 멀티 모드 모델 -Anuctics VidhyaApr 13, 2025 am 11:20 AM
Pixtral -12B : Mistral AI의 첫 번째 멀티 모드 모델 -Anuctics VidhyaApr 13, 2025 am 11:20 AM소개 Mistral은 최초의 멀티 모드 모델, 즉 Pixtral-12B-2409를 발표했습니다. 이 모델은 Mistral의 120 억 개의 매개 변수 인 NEMO 12B를 기반으로합니다. 이 모델을 차별화하는 것은 무엇입니까? 이제 이미지와 Tex를 모두 가져갈 수 있습니다
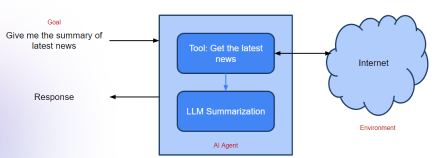 생성 AI 응용 프로그램을위한 에이전트 프레임 워크 - 분석 VidhyaApr 13, 2025 am 11:13 AM
생성 AI 응용 프로그램을위한 에이전트 프레임 워크 - 분석 VidhyaApr 13, 2025 am 11:13 AM쿼리에 응답 할뿐만 아니라 자율적으로 정보를 모으고, 작업을 실행하며, 여러 유형의 데이터 (텍스트, 이미지 및 코드를 처리하는 AI 구동 조수가 있다고 상상해보십시오. 미래처럼 들리나요? 이것에서
 금융 부문에서 생성 AI의 응용Apr 13, 2025 am 11:12 AM
금융 부문에서 생성 AI의 응용Apr 13, 2025 am 11:12 AM소개 금융 산업은 효율적인 거래 및 신용 가용성을 촉진함으로써 경제 성장을 주도하기 때문에 모든 국가 개발의 초석입니다. 거래가 발생하는 용이성 및 신용
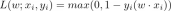 온라인 학습 및 수동 공격 알고리즘 안내Apr 13, 2025 am 11:09 AM
온라인 학습 및 수동 공격 알고리즘 안내Apr 13, 2025 am 11:09 AM소개 소셜 미디어, 금융 거래 및 전자 상거래 플랫폼과 같은 소스에서 전례없는 속도로 데이터가 생성되고 있습니다. 이 지속적인 정보 스트림을 처리하는 것은 어려운 일이지만


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

Atom Editor Mac 버전 다운로드
가장 인기 있는 오픈 소스 편집기

Eclipse용 SAP NetWeaver 서버 어댑터
Eclipse를 SAP NetWeaver 애플리케이션 서버와 통합합니다.

PhpStorm 맥 버전
최신(2018.2.1) 전문 PHP 통합 개발 도구

드림위버 CS6
시각적 웹 개발 도구

mPDF
mPDF는 UTF-8로 인코딩된 HTML에서 PDF 파일을 생성할 수 있는 PHP 라이브러리입니다. 원저자인 Ian Back은 자신의 웹 사이트에서 "즉시" PDF 파일을 출력하고 다양한 언어를 처리하기 위해 mPDF를 작성했습니다. HTML2FPDF와 같은 원본 스크립트보다 유니코드 글꼴을 사용할 때 속도가 느리고 더 큰 파일을 생성하지만 CSS 스타일 등을 지원하고 많은 개선 사항이 있습니다. RTL(아랍어, 히브리어), CJK(중국어, 일본어, 한국어)를 포함한 거의 모든 언어를 지원합니다. 중첩된 블록 수준 요소(예: P, DIV)를 지원합니다.







