html5 캔버스 그리기 튜토리얼(6) - canvas_html5 튜토리얼 기술에서 곡선을 그리기 위한 arcTo 메소드

이전 글에서는 캔버스의 arc 메소드에 대해 이야기했고, 이번 글에서는 이와 관련된 arcTo 메소드에 대해 이야기합니다.
arc와 arcTo는 이름부터 비슷합니다. arcTo 역시 곡선을 그리는 방법이고, 그가 그리는 곡선 역시 완벽한 원의 호이다. 그러나 그의 매개변수는 arc~
ctx.arcTo(x1,y1,x2,y2,radius); 와 호환되지 않습니다. arcTo의 매개변수는 두 개의 점을 포함하며 이 두 점은 원의 중심을 나타내지 않습니다. 마지막 매개변수만 원의 반경이며, 이는 arcTo가 원과 어떤 관계가 있음을 나타냅니다.
arcTo에 대한 인터넷 기사는 거의 없고, 마침내 외국에서 기사를 찾았으며, 캔버스 그리기에 대한 직관적인 도구가 없기 때문에 오랫동안 추측에만 의존할 수 있었습니다. . .
직관적인 설명을 위해 보조 방법을 채택했습니다. arcTo가 그려지는 곳마다 lineTo를 사용하여 해당 점을 그려서 관계를 확인합니다. 보조선을 그어주시면 됩니다.

코드 복사

코드는 다음과 같습니다.

var x0=100,
y0 =400,
x1 = 500,
y1 = 400,
x2 = 450,
y2 = 450;
ctx.beginPath()
ctx.moveTo( x0,y0);
ctx.StrokeStyle = "#f00";
ctx.lineWidth = 2
ctx.arcTo(x1,y1,x2,y2,20); ();
ctx.beginPath();
ctx.StrokeStyle = "rgba(0,0,0,0.5)"
ctx.lineWidth = 1
ctx.moveTo; y0);
ctx.lineTo(x1,y1);
ctx.fillText('x1,y1',x1 10,y1 10)
ctx.lineTo(x2,y2); .fillText( 'x2,y2',x2 10,y2)
ctx.Stroke();


코드가 많아 보이지만 실제로는 매우 간단합니다. 좌표 값을 저장하기 위해 몇 가지 변수를 사용했고 나머지는 캔버스 작업이었습니다.

변수 설명: x0, y0은 시작점의 좌표, x1, y1은 첫 번째 점의 좌표, x2, y2는 두 번째 점의 좌표입니다. lineTo로 그린 직선은 반투명한 1px의 검은색 선이고, arcTo로 그린 선은 2px의 빨간색 선입니다.
페이지를 새로고침하시면 아래 사진을 보실 수 있습니다.

이 빨간 선은 고리처럼 보인다고 해야 할까요.

그러면 arcTo의 규칙이 발견됩니다. 이는 실제로 시작점, 첫 번째 점, 두 번째 점에서 두 개의 직선을 통과하여 끼인각을 형성하며 이 두 선도 매개변수 원에 접합니다.
원의 반경에 따라 원이 선에 접하는 위치가 결정됩니다. 공이 사각지대에 굴러가는 것과 마찬가지로, 공이 작을수록 더 멀리 굴러가고 사각지대에 가까워집니다. 더 큰 공의 경우에는 그 반대입니다.
이건 매우 심각한 학문적 문제입니다. YY처럼 말하지 마세요.
공을 더 크게 만들어보자!

코드 복사코드는 다음과 같습니다.

ctx.arcTo(x1, y1,x2 ,y2,50); //반경을 50으로 변경

사진과 같이 호가 매우 크게 되어 직선에 접하지도 않는 것을 볼 수 있습니다.

물론 접선이 무한히 연장되기 때문에 실제로는 여전히 접선입니다.
우리는 계속 탐색하고, 계속해서 원을 더 크게 만들고, 시작점과 첫 번째 지점 사이의 거리를 줄입니다.

코드 복사코드는 다음과 같습니다.

var x0=400; /시작점 x 좌표가 100에서 400으로 변경됩니다.

...
ctx.arcTo(x1,y1,x2,y2,100) //원의 반경이 100으로 증가하면 다음과 같이 표시됩니다. 정말 이상한 모양.

원래는 갈고리였는데 지금은 갑자기 휘어졌고 심지어 반대방향으로도! 와인병걸이와 비슷하네요. 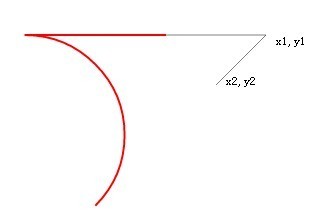그러나 이 원은 여전히 ​​두 선에 접해 있다는 점에 유의하세요! 이제 두 선의 길이가 원을 만날 수 없습니다! 그는 두 회선을 모두 무선으로 확장했습니다!

이 후크 손잡이는 언제 반전되나요? 기하학에 능숙하다면 점과 원 사이의 접선 방정식을 이해하려고 노력할 수 있습니다.
arcTo 메소드에는 매우 중요한 점이 있습니다. 이 중요한 점은 원의 접선점까지의 거리가 시작점(x0, y0)까지의 거리를 초과하는 한 코드에서 (x1, y1)입니다. ), 반전이 발생합니다.
그림에서 볼 수 있듯이 점(x2, y2)의 좌표는 항상 접선 위의 점인 한 원의 반지름이 변하지 않으면 그래프가 그려집니다. by arcTo 아무것도 변하지 않습니다. 이는 특별한 주의가 필요합니다.
이 명제를 검증하기 위해 탁자 위에는 없는 기하학에 대한 나의 지식을 활용하겠습니다. 계산을 쉽게 하기 위해 먼저 두 선 사이의 각도를 90도로 변경합니다.

코드 복사코드는 다음과 같습니다.

var x0=100,
y0=400,
x1 = 500,
y1 = 400,
x2 = 500,
y2 = 450; 🎜>
변경 후 90도로 열리네요! 공의 반경을 일정하게 유지합니다. 새로 고침 후:

y2를 더 크게 만듭니다. 즉, 접선을 연장하여 550으로 바꿉니다. 새로 고친 후: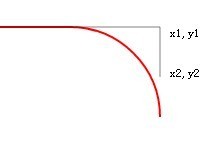

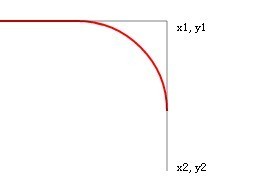접선은 연장되었으나 arcTo로 그린 빨간색 선은 변화가 없습니다.