데이터 분포의 정규성을 결정하는 11가지 기본 방법

데이터 과학 및 기계 학습 분야에서 많은 모델은 데이터가 정규 분포를 따르거나 정규 분포에서 데이터 성능이 더 좋다고 가정합니다. 예를 들어 선형회귀는 잔차가 정규분포를 따른다고 가정하고, 선형판별분석(LDA)은 정규분포와 같은 가정을 바탕으로 도출됩니다. 따라서 데이터 과학자와 머신러닝 실무자에게는 데이터의 정규성을 테스트하는 방법을 이해하는 것이 중요합니다

이 글에서는 독자가 데이터 분포의 특성을 더 잘 이해하고 학습할 수 있도록 데이터의 정규성을 테스트하는 11가지 기본 방법을 소개하는 것을 목표로 합니다. 분석에 적절한 방법을 적용하는 방법. 이는 데이터 분포가 모델 성능에 미치는 영향을 더 잘 처리할 수 있으며 기계 학습 및 데이터 모델링 과정에서 더 편안해질 수 있습니다

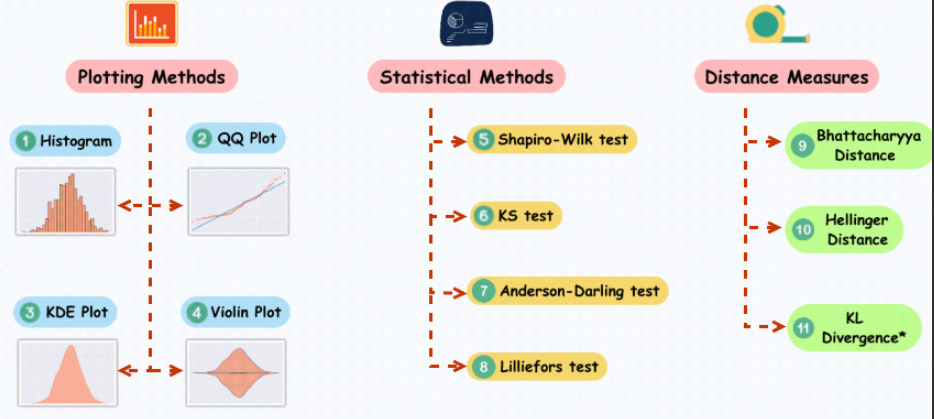
Plotting Methods

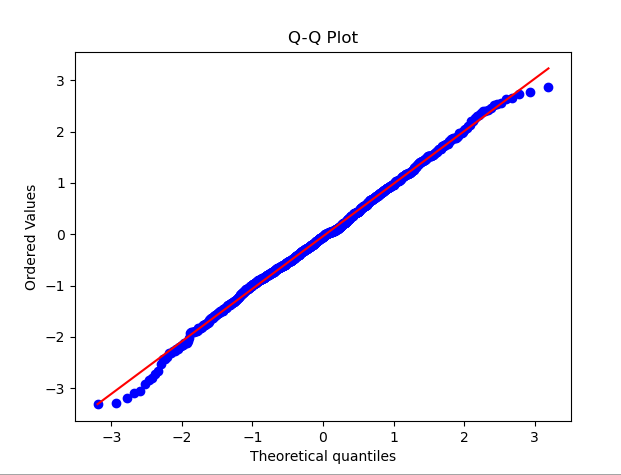
1. 분포는 정규분포를 따른다. QQ 플롯에서 데이터의 분위수는 표준 정규 분포의 분위수와 비교됩니다. 데이터 분포가 정규 분포에 가까우면 QQ 플롯의 점은 직선에 가까워집니다

QQ 플롯, 다음 샘플 코드는 정규 분포를 따르는 임의의 데이터 집합을 생성합니다. 코드를 실행하면 해당 정규 분포 곡선과 함께 QQ 플롯을 볼 수 있습니다. 그래프의 점 분포를 관찰하면 데이터가 정규 분포에 가까운지 여부를 초기에 판단할 수 있습니다

import numpy as npimport scipy.stats as statsimport matplotlib.pyplot as plt# 生成一组随机数据，假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制QQ图stats.probplot(data, dist="norm", plot=plt)plt.title('Q-Q Plot')plt.show()

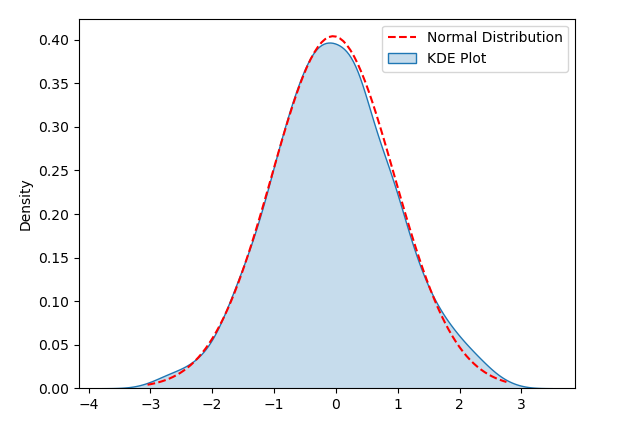
2. KDE Plot

KDE(Kernel Density Estimation) 플롯은 데이터 분포를 시각화하는 방법입니다. 우리는 데이터의 정규성을 테스트했습니다. KDE 플롯에서는 데이터의 밀도를 추정하고 이를 부드러운 곡선으로 그려 데이터의 분포 형태를 관찰하는 데 도움이 됩니다.

KDE 플롯을 시연하기 위해 다음 샘플 코드는 다음 샘플 코드를 준수하는 임의의 데이터 세트를 생성합니다. 정규 분포. 코드를 실행하면 KDE Plot과 해당 정규 분포 곡선을 볼 수 있으며 시각화를 사용하여 데이터 분포가 정규성을 준수하는지 감지할 수 있습니다

import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=1000)# 创建KDE Plotsns.kdeplot(data, shade=True, label='KDE Plot')# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()

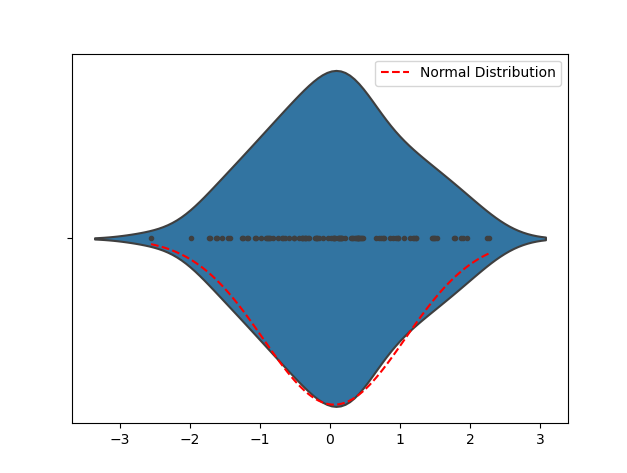
3. Violin Plot

데이터 분포를 확인할 수 있습니다. Violin Plot 모양을 관찰하여 데이터가 정규 분포에 가까운지 여부를 초기에 확인합니다. 바이올린 플롯이 종형 곡선 모양을 취하는 경우 데이터는 대략 정규 분포를 따릅니다. 바이올린 플롯이 심하게 치우쳐 있거나 여러 개의 피크가 있는 경우 데이터가 정규 분포를 따르지 않을 수 있습니다.

다음 예제 코드는 바이올린 플롯을 보여주기 위해 정규 분포에 따라 임의의 데이터를 생성하는 데 사용됩니다. 코드를 실행하면 Violin Plot과 해당 정규 분포 곡선을 볼 수 있습니다. 시각화를 통해 데이터 분포의 형태를 검출하여 데이터가 정규 분포에 가까운지 초기 판단

import numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# 生成随机数据np.random.seed(0)data = np.random.normal(loc=0, scale=1, size=100)# 创建 Violin Plotsns.violinplot(data, inner="points")# 添加正态分布曲线mu, sigma = np.mean(data), np.std(data)x = np.linspace(min(data), max(data), 100)y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)plt.plot(x, y, 'r--', label='Normal Distribution')# 显示图表plt.legend()plt.show()

4.Histogram

데이터 분포의 정규성을 검출하기 위해 히스토그램(Histogram)을 사용하는 것도 일반적입니다. 방법. 히스토그램은 데이터의 분포를 직관적으로 이해하는 데 도움을 줄 수 있으며, 데이터가 정규분포에 가까운지 사전에 판단할 수 있습니다

import numpy as npimport matplotlib.pyplot as pltimport scipy.stats as stats# 生成一组随机数据，假设它们服从正态分布data = np.random.normal(0, 1, 1000)# 绘制直方图plt.hist(data, bins=30, density=True, alpha=0.6, color='g')plt.title('Histogram of Data')plt.xlabel('Value')plt.ylabel('Frequency')# 绘制正态分布的概率密度函数xmin, xmax = plt.xlim()x = np.linspace(xmin, xmax, 100)p = stats.norm.pdf(x, np.mean(data), np.std(data))plt.plot(x, p, 'k', linewidth=2)plt.show()

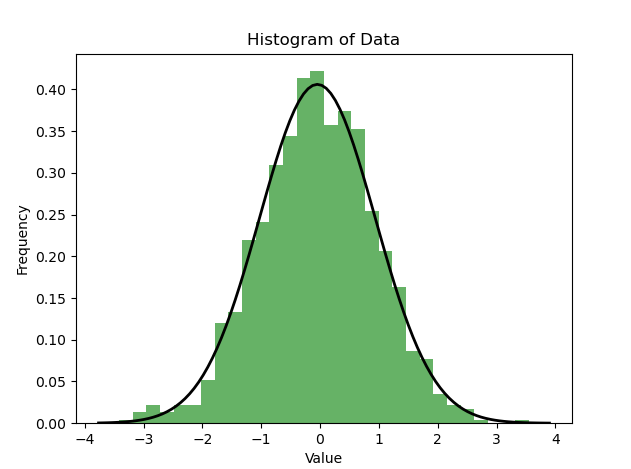위 그림과 같이 히스토그램이 대략 종 모양의 곡선을 나타내고, 해당 정규 분포와 일치합니다. 곡선 모양이 유사하면 데이터가 정규 분포를 따를 가능성이 높습니다. 물론, 시각화는 단지 예비적인 판단일 뿐이며, 보다 정확한 검출이 필요한 경우에는 정규성 테스트와 같은 통계적 방법을 사용하여 분석할 수 있습니다.

통계 방법

5. Shapiro-Wilk 테스트

Shapiro-Wilk 테스트는 데이터가 정규 분포를 따르는지 테스트하는 데 사용되는 통계 방법으로, W 테스트라고도 합니다. Shapiro-Wilk 테스트를 수행할 때 일반적으로 두 가지 주요 지표에 중점을 둡니다.

통계 W: 관측 데이터와 정규 분포 하의 기대 값 사이의 상관 관계를 기반으로 통계 W를 계산하고 W 사이의 값 범위 0과 1, W가 1에 가까울수록 관측된 데이터가 정규 분포에 더 잘 맞는다는 의미입니다.

• P 값: P 값은 이 상관 관계를 관찰할 가능성을 나타냅니다. P 값이 유의 수준(보통 0.05)보다 크면 관찰된 데이터가 정규 분포에서 나올 가능성이 있음을 나타냅니다.
• 따라서 통계 W가 1에 가까우며 P 값이 0.05보다 크면 관측된 데이터가 정규 분포를 만족한다는 결론을 내릴 수 있습니다.

다음 코드에서는 먼저 정규 분포를 따르는 임의의 데이터 집합을 생성한 후 Shapiro-Wilk 테스트를 수행하여 테스트 통계량과 P 값을 얻습니다. P 값과 유의 수준의 비교를 기반으로 표본 데이터가 정규 분포에서 나온 것인지 여부를 확인할 수 있습니다.

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk检验stat, p = stats.shapiro(data)print('Shapiro-Wilk Statistic:', stat)print('P-value:', p)# 根据P值判断正态性alpha = 0.05if p > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

6.KS检验

KS检验（Kolmogorov-Smirnov检验）是一种用于检验数据是否符合特定分布（例如正态分布）的统计方法。它通过计算观测数据与理论分布的累积分布函数（CDF）之间的最大差异来评估它们是否来自同一分布。其基本步骤如下：

• 对两个样本数据进行排序。
• 计算两个样本的经验累积分布函数(ECDF)，即计算每个值在样本中的累积百分比。
• 计算两个累积分布函数之间的差异，通常使用KS统计量衡量。
• 根据样本的大小和显著性水平，使用参考表活计算p值判断两个样本是否来自同一分布。

Python中使用KS检验来检验数据是否符合正态分布时，可以使用Scipy库中的kstest函数。下面是一个简单的示例，演示了如何使用Python进行KS检验来检验数据是否符合正态分布。

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行KS检验statistic, p_value = stats.kstest(data, 'norm')print('KS Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

7.Anderson-Darling检验

Anderson-Darling检验是一种用于检验数据是否来自特定分布（例如正态分布）的统计方法。它特别强调观察值在分布尾部的差异，因此在检测极端值的偏差方面非常有效

下面的代码使用stats.anderson函数执行Anderson-Darling检验，并获取检验统计量、临界值以及显著性水平。然后通过比较统计量和临界值，可以判断样本数据是否符合正态分布

from scipy import statsimport numpy as np# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Anderson-Darling检验result = stats.anderson(data, dist='norm')print('Anderson-Darling Statistic:', result.statistic)print('Critical Values:', result.critical_values)print('Significance Level:', result.significance_level)# 判断正态性if result.statistic <p style="text-align:center;"><img src="https://img.php.cn/upload/article/000/887/227/170255826239547.png" alt="데이터 분포의 정규성을 결정하는 11가지 기본 방법"></p><h4>8.Lilliefors检验</h4><p>Lilliefors检验（也被称为Kolmogorov-Smirnov-Lilliefors检验）是一种用于检验数据是否符合正态分布的统计检验方法。它是Kolmogorov-Smirnov检验的一种变体，专门用于小样本情况。与K-S检验不同，Lilliefors检验不需要假定数据的分布类型，而是基于观测数据来评估是否符合正态分布</p><p>在下面的例子中，我们使用lilliefors函数进行Lilliefors检验，并获得了检验统计量和P值。通过将P值与显著性水平进行比较，我们可以判断样本数据是否符合正态分布</p><pre class="brush:php;toolbar:false">import numpy as npfrom statsmodels.stats.diagnostic import lilliefors# 生成一组服从正态分布的随机数据data = np.random.normal(0, 1, 100)# 执行Lilliefors检验statistic, p_value = lilliefors(data)print('Lilliefors Statistic:', statistic)print('P-value:', p_value)# 根据P值判断正态性alpha = 0.05if p_value > alpha:print('样本数据可能来自正态分布')else:print('样本数据不符合正态分布')

9.距离测量Distance Measures

距离测量（Distance measures）是一种有效的测试数据正态性的方法，它提供了更直观的方式来比较观察数据分布与参考分布之间的差异。

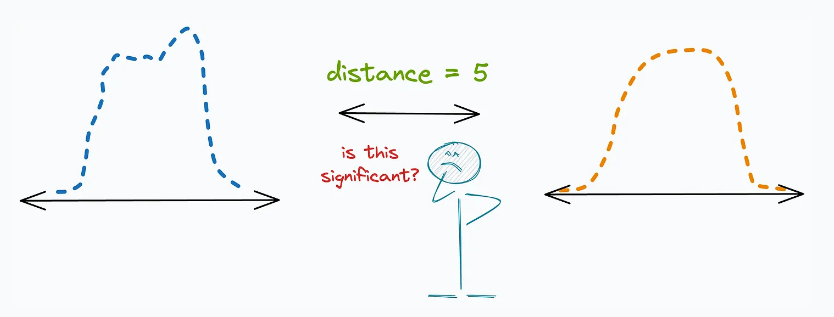
下面是一些常见的距离测量方法及其在测试正态性时的应用：

(1) "巴氏距离（Bhattacharyya distance）"的定义是：

• 测量两个分布之间的重叠，通常被解释为两个分布之间的接近程度。
• 选择与观察到的分布具有最小Bhattacharyya距离的参考分布，作为最接近的分布。

(2) 「海林格距离（Hellinger distance）」：

• 用于衡量两个分布之间的相似度，类似于Bhattacharyya距离。
• 与Bhattacharyya距离不同的是，Hellinger距离满足三角不等式，这使得它在一些情况下更为实用。

(3) "KL 散度（KL Divergence）"：

• 它本身并不是严格意义上的“距离度量”，但在测试正态性时可以用作衡量信息丢失的指标。
• 选择与观察到的分布具有最小KL散度的参考分布，作为最接近的分布。

运用这些距离测量方法，我们能够比对观测到的分布与多个参考分布之间的差异，进而更好地评估数据的正态性。通过找出与观察到的分布距离最短的参考分布，我们可以更精确地判断数据是否符合正态分布

위 내용은 데이터 분포의 정규성을 결정하는 11가지 기본 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!