머신러닝 애플리케이션에서 일반적으로 사용되는 회귀 알고리즘과 그 특성
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-11-29 17:29:261008검색
회귀는 통계에서 가장 강력한 도구 중 하나입니다. 기계 학습 지도 학습 알고리즘은 분류 알고리즘과 회귀 알고리즘의 두 가지 유형으로 나뉩니다. 회귀 알고리즘은 연속 분포 예측에 사용되며 개별 범주 레이블이 아닌 연속 데이터를 예측할 수 있습니다.
회귀 분석은 제품 판매 예측, 교통 흐름, 주택 가격, 기상 조건 등 기계 학습 분야에서 널리 사용됩니다. 회귀 알고리즘은 일반적으로 사용되는 기계 학습 알고리즘으로, 두 항목 간의 관계를 설정하는 데 사용됩니다. 독립변수 X와 종속변수 Y 관계. 기계 학습 관점에서 속성 X와 레이블 Y 간의 매핑 관계를 달성하기 위해 알고리즘 모델(함수)을 구축하는 데 사용됩니다. 학습 과정에서 알고리즘은 최적의 매개변수 관계를 찾으려고 노력합니다. 회귀 알고리즘에서 알고리즘(함수)의 최종 결과는 연속적인 데이터 값입니다. 입력값(속성값)은 d차원 속성/숫자 벡터입니다일반적으로 사용되는 회귀 알고리즘에는 선형 회귀, 다항식 회귀, 의사결정 트리 회귀, Ridge 회귀, Lasso 회귀, ElasticNet 회귀 등이 있습니다.이 문서에서는 몇 가지 일반적인 회귀 알고리즘과 해당 특성을 소개합니다.의사결정 트리 회귀
- Random 숲이 돌아왔습니다
- LASSO가 돌아왔습니다
- Ridge가 돌아왔습니다
- ElasticNet이 돌아왔습니다
- X GBoost가 돌아왔습니다
- 로컬 가중 선형 회귀
- One , 선형 회귀 선형 회귀는 사람들이 기계 학습과 데이터 과학에 대해 배우는 첫 번째 알고리즘인 경우가 많습니다. 선형 회귀는 입력 변수(X)와 단일 출력 변수(y) 사이의 선형 관계를 가정하는 선형 모델입니다. 일반적으로 두 가지 상황이 있습니다.
- 일변량 선형 회귀는 단일 입력 변수(즉, 단일 특성 변수)와 단일 출력 변수 간의 관계를 분석하는 데 사용되는 모델링 방법입니다.
- 다변수 선형 회귀(또한 다중 선형 회귀라고 함): 여러 입력 변수(다중 특성 변수)와 단일 출력 변수 간의 관계를 모델링합니다. 선형 회귀에 대한 몇 가지 핵심 사항:
- 빠르고 쉬운 모델링
매우 직관적인 이해와 설명입니다.
이상값에 매우 민감합니다.
2. 다항식 회귀
비선형 분리 가능한 데이터에 대한 모델을 만들 때 다항식 회귀는 가장 인기 있는 선택 중 하나입니다. 선형 회귀와 유사하지만 변수 X와 y 사이의 관계를 사용하여 데이터 포인트에 맞는 곡선을 그리는 가장 좋은 방법을 찾습니다.
- 다항식 회귀에 대한 몇 가지 핵심 사항:
- 선형 회귀 분석에서는 이를 수행할 수 없습니다. 일반적으로 이는 더 유연하며 상당히 복잡한 관계를 모델링할 수 있습니다.
- 특징 변수(설정할 지수) 모델링을 완벽하게 제어합니다.
- 신중한 디자인이 필요합니다. 최상의 인덱스를 선택하려면 일부 데이터 지식이 필요합니다.
3. 지원 벡터 머신 회귀
지원 벡터 머신은 분류 문제에서 잘 알려져 있습니다. 회귀에서 SVM을 사용하는 것을 지원 벡터 회귀(SVR)라고 합니다. Scikit-learn에는 SVR()에 이 메서드가 내장되어 있습니다.
- 서포트 벡터 회귀에 대한 몇 가지 핵심 사항:
- 이상치에 강력하고 고차원 공간에서 효과적입니다.
- 탁월한 일반화 기능(새로운, 이전에 올바르게 적응하는 능력) 보이지 않는 데이터)
4. 결정 트리 회귀
결정 트리는 비-분류 및 회귀에 사용되는 방법입니다. 파라메트릭 지도 학습 방법. 목표는 데이터 특징에서 유추되는 간단한 의사결정 규칙을 학습하여 대상 변수의 값을 예측하는 모델을 만드는 것입니다. 트리는 조각별 상수 근사로 볼 수 있습니다.
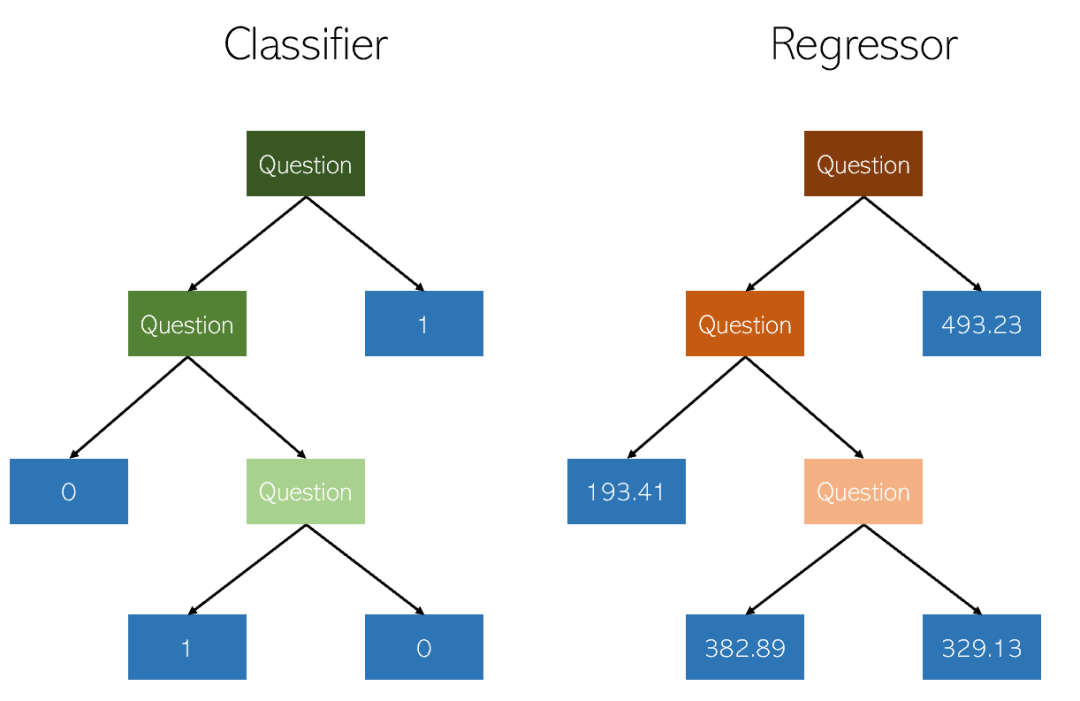
의사결정 트리에 대한 몇 가지 핵심 사항:
- 이해하고 설명하기 쉽습니다. 나무를 시각화할 수 있습니다.
- 범주형 값과 연속형 값 모두에 적용됩니다.
- DT(예: 예측 데이터) 사용 비용은 트리를 훈련하는 데 사용된 데이터 포인트 수에 대한 대수적입니다.
- 의사결정 트리의 예측은 부드럽지도 않고 부드럽지도 않습니다. 연속형 (위 그림과 같이 조각상 상수 근사치임)
5. Random Forest Regression
Random Forest Regression과 Decision Tree Regression은 기본적으로 매우 유사합니다. 이는 데이터 세트의 다양한 하위 샘플에 여러 의사결정 트리를 적용하고 이를 평균화하여 예측 정확도를 향상하고 과적합을 제어할 수 있는 메타 추정기입니다.
회귀 문제의 Random Forest Regressor 성능은 의사결정 트리보다 좋을 수도 있고 나쁠 수도 있습니다. 분류 문제에서 더 좋음) 트리 구성 알고리즘에 내재된 미묘한 과적합 및 과소적합 절충으로 인해
Random Forest 정보 회귀에 대한 몇 가지 사항:
- 결정 트리의 과적합을 줄이고 정확도를 향상시킵니다.
- 범주형 값과 연속형 값에도 적용됩니다.
- 출력을 결합하려면 많은 의사결정 트리에 적합하므로 많은 컴퓨팅 성능과 리소스가 필요합니다.
6. LASSO 회귀
LASSO 회귀는 수축 선형 회귀의 변형입니다. 축소란 데이터 값을 평균으로 중심점으로 축소하는 과정입니다. 이러한 유형의 회귀는 심각한 다중 공선성(특성 간 상관 관계가 높음)이 있는 모델에 이상적입니다.
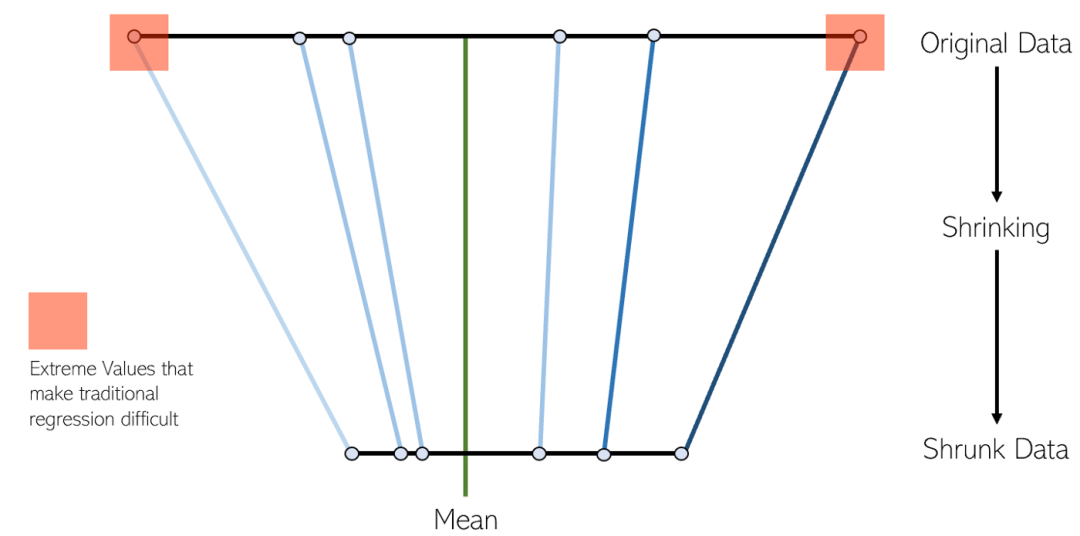
Lasso 회귀에 대한 몇 가지 사항:
- 자동 변수를 제거하고 특성을 선택하는 데 가장 일반적으로 사용됩니다. .
- 심각한 다중 공선성을 나타내는 모델에 이상적입니다(특성이 서로 높은 상관 관계를 갖고 있음).
- LASSO 회귀는 L1 정규화를 활용합니다.
- LASSO 회귀는 일부 기능만 선택하고 다른 기능의 계수를 0으로 줄이므로 Ridge보다 더 나은 것으로 간주됩니다.
7. 능선 회귀
능선 회귀는 두 기술 모두 축소 방법을 사용하므로 LASSO 회귀와 매우 유사합니다. Ridge 회귀와 LASSO 회귀는 모두 심각한 다중 공선성 문제(즉, 특성 간의 높은 상관 관계)가 있는 모델에 매우 적합합니다. 둘 사이의 주요 차이점은 Ridge가 L2 정규화를 사용한다는 것입니다. 즉, LASSO 회귀와 같이 어떤 계수도 0이 되지는 않습니다(그러나 0에 가깝습니다). Ridge 회귀에 대한 몇 가지 사항:
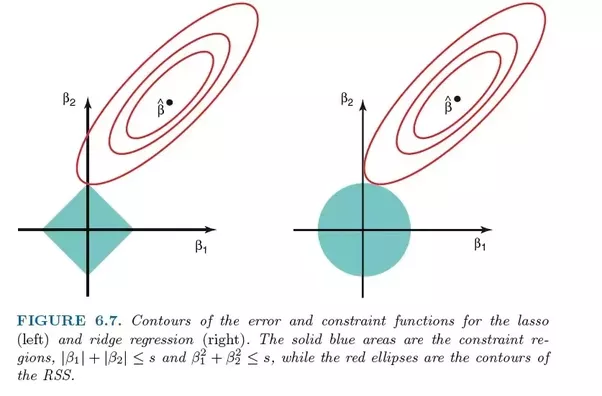
심각한 다중 공선성을 나타내는 모델에 이상적입니다(특성이 서로 높은 상관 관계를 갖고 있음).
Ridge 회귀는 L2 정규화를 사용합니다. 덜 기여하는 기능은 0에 가까운 계수를 갖게 됩니다.- 능형 회귀는 L2 정규화의 특성으로 인해 LASSO보다 나쁜 것으로 간주됩니다.
- 8. ElasticNet 회귀
- ElasticNet은 L1 및 L2 정규화를 사용하여 훈련된 또 다른 선형 회귀 모델입니다. Lasso 회귀분석과 Ridge 회귀분석 기법을 혼합한 것이기 때문에 다중공선성이 심한(특징이 서로 높은 상관관계가 있음) 모델에도 적합합니다.
Lasso와 Ridge 사이에 무게를 둘 때 실용적인 이점은 Elastic-Net이 회전 시 Ridge의 안정성 중 일부를 상속받을 수 있다는 것입니다.
9 XGBoost Regression
XGBoost는 그래디언트 부스팅 알고리즘의 효율적인 버전입니다. 효과적으로 구현되었습니다. Gradient Boosting은 분류 또는 회귀 문제에 사용할 수 있는 앙상블 기계 학습 알고리즘의 한 유형입니다
XGBoost는 원래 Chen Tianqi가 2016년 논문 "XGBoost: A Scalable Tree Boosting System"에서 개발한 오픈 소스 라이브러리입니다. 알고리즘은 계산적으로 효율적이고 효율적으로 설계되었습니다
XGBoost에 대한 몇 가지 사항:
- XGBoost는 희박하고 구조화되지 않은 데이터에서는 제대로 작동하지 않습니다.
- 알고리즘은 계산적으로 효율적이고 효율적으로 설계되었지만 대규모 데이터 세트의 경우 훈련 시간이 여전히 상당히 깁니다.
- 이상치에 민감합니다.
10. Local Weighted Linear Regression
Local Weights Linear Regression(로컬 가중치 선형 회귀)에서는 선형 회귀도 수행합니다. 그러나 일반 선형회귀와는 달리 국소가중선형회귀는 국소선형회귀 방법이다. 가중치(커널 함수)를 도입함으로써 예측 시 테스트 포인트에 가까운 일부 샘플만 회귀 계수를 계산하는 데 사용됩니다. 일반적인 선형회귀는 전역선형회귀인데, 모든 표본을 이용하여 회귀계수를 계산합니다
장점과 단점 & 적용 가능한 시나리오
장점은 커널 함수 가중치를 통해 과소적합을 방지하는 것이고, 단점도 뻔합니다K 디버깅 필요합니다. 다중 선형 회귀가 과적합되는 경우 가우스 커널 로컬 가중치를 사용하여 과적합을 방지할 수 있습니다.
11. 베이지안 능형 회귀
베이지안 추론 방법을 사용하여 풀어낸 선형 회귀 모델을 베이지안 선형 회귀라고 합니다
베이지안 선형 회귀는 선형 모델의 매개변수를 확률변수로 처리하고 이전 것으로부터 사후를 계산합니다. 베이지안 선형회귀는 수치적 방법으로 풀 수 있으며 특정 조건에서는 분석적 형태의 사후 또는 관련 통계도 얻을 수 있습니다
베이지안 선형회귀는 베이지안 통계 모형의 기본 특성을 가지며 가중치 계수에 대해 풀 수 있습니다. 확률 밀도 함수 , Bayes 요인(Bayes 요인)을 기반으로 한 온라인 학습 및 모델 가설 테스트
장점과 단점 및 적용 가능한 시나리오
베이지안 회귀의 장점은 데이터 적응성이며, 데이터를 재사용하고 과적합을 방지할 수 있습니다. 추정 과정에서 정규화 항을 도입할 수 있는데, 예를 들어 베이지안 선형 회귀에 L2 정규화 항을 도입하면 베이지안 능선 회귀를 구현할 수 있는데, 학습 과정이 너무 비싸다는 단점이 있습니다. 특성 수가 10개 미만인 경우 베이지안 회귀를 시도할 수 있습니다.
위 내용은 머신러닝 애플리케이션에서 일반적으로 사용되는 회귀 알고리즘과 그 특성의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

