Terence Tao의 Crazy Amway Copilot: 한 페이지 분량의 교정을 완료하고 후속 프로세스를 추측하는 데 도움이 되었습니다.
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-10-23 11:13:11934검색
Copilot은 GPT-4의 "승인"을 받은 후 Terence Tao의 선호를 받았습니다.
코파일럿은 프로그래밍을 할 때 자신이 다음에 무엇을 할지 직접 예측할 수 있다고 직설적으로 말했습니다.
Copilot을 사용하면 연구가 더욱 편리해졌습니다. Tao Zhexuan도 이를 사용하여 최신 연구 결과를 완성했습니다.

Tao Zhexuan은 이 부분이 실제로 한 페이지밖에 없다고 말했습니다.
하지만 이 한 페이지짜리 증명을 완성하기 위해 그는 새로 배운 프로그래밍 언어 Lean4를 사용하여 200줄이 넘는 코드를 작성했습니다.

Tao Zhexuan의 공개 코드 GitHub 페이지에는 Copilot이 코드 작성 속도를 절반 이상 높인 것으로 나타났습니다.
Tao Zhexuan은 Lean4를 선택한 이유가 긴 표현의 타겟 부분 교체를 수행하는 "다시 쓰기 전략" 때문이라고 말했습니다.
예를 들어, 복잡한 함수 f(x)가 정의된 경우 f(114514)의 표현식을 입력하려고 할 때 코드를 사용하여 x를 114514로 직접 "다시 쓸" 수 있습니다.
Tao Zhexuan은 이 기능이 수식을 반복적으로 입력해야 하는 LaTeX에 비해 그다지 편리하지 않다고 말했습니다.
그렇다면 이번에 도저쉬안의 '한 페이지 증명'은 우리에게 어떤 새로운 결과를 가져다 주었나요?
새로운 불평등에 대한 한 페이지의 증명
이 문서에서는 MacLaughlin의 불평등과 관련된 문제에 대해 설명합니다.
McLaughlin의 부등식은 수학의 고전적인 부등식으로, "음이 아닌 실수의 산술 평균은 기하 평균보다 크거나 같다"는 법칙에 기초하여 도출됩니다.
y를 가정합니다. 1...yn 은 음수가 아닌 실수입니다. k=1...n의 경우 평균 Sk은 다음과 같이 정의됩니다(분모는 분자의 항 수).
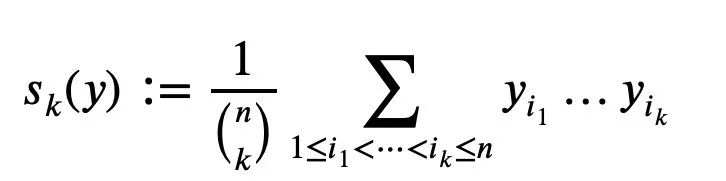
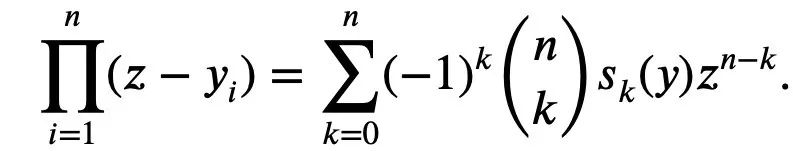
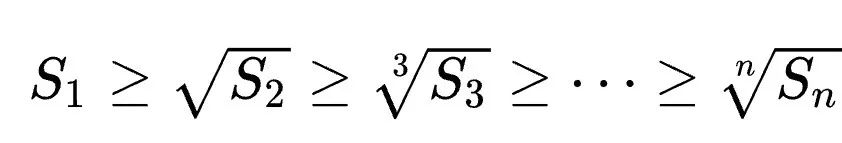
모든 1≤k
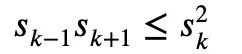
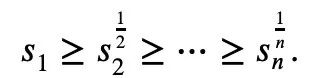
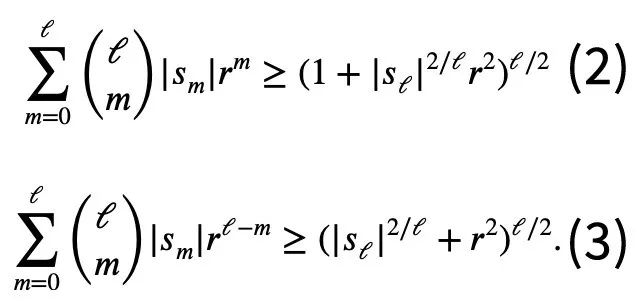
따라서 하한값만 설정하면 됩니다.
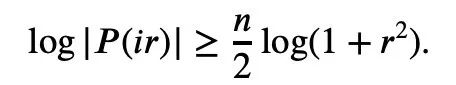
P(z)의 절대값을 취하고 로그를 취하여 다음을 얻습니다.
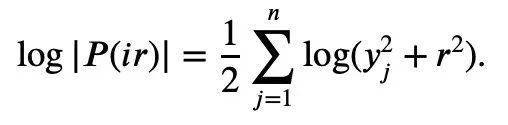
실수 t에 대해 t ↦ log(e t+a)는 Convexity이고 a>0이면 부등식을 얻을 수 있습니다.
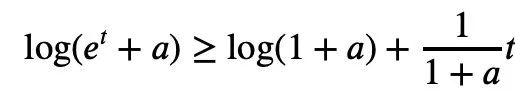
a=r2, t=2log yj일 때 다음을 얻을 수 있습니다.
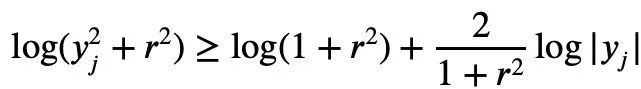
The 위는 Tao Zhexuan이 제공한 증명 프로세스이지만 정규화된 |Sn|=1인 경우 다음 공식이 유지됩니다.
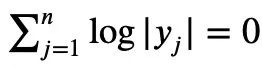
다음 단계: 세련된 버전 만들기
"one- pageproof"에서 이번에 언급한 Terence Tao의 이 논문은 또 다른 새로운 정리, 즉 임의의 1 ≤ k ≤ ℓ≤ n에 대해 제안했습니다.:
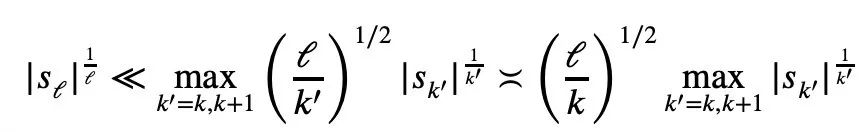
블로그 게시물에서 Tao Zhexuan은 다음 계획은 다음과 같다고 밝혔습니다. 이 불평등 개선 버전을 제안합니다.
Tao Zhexuan은 증명 과정이 연습만큼 간단하고 미적분학으로 이루어질 수 있다고 말했습니다.
그러나 이 부분은 점근 기호를 사용하기 때문에 약간의 어려움이 있을 것이라고 언급했습니다.

어떤 새로운 결론이 나올지 지켜보겠습니다.
한 가지 더
Tao Zhexuan은 Copilot, GPT-4 및 기타 보조 도구의 열렬한 팬입니다.
이번에는 모델이 직접 불평등 변형을 생성할 수 있는 날이 오기를 바라며 대형 모델 개발에 대한 새로운 기대도 제시했습니다.

문서 주소: https://arxiv.org/abs/2310.05328
위 내용은 Terence Tao의 Crazy Amway Copilot: 한 페이지 분량의 교정을 완료하고 후속 프로세스를 추측하는 데 도움이 되었습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

