그래프의 주요 집합이 NP-완전임을 증명
- PHPz앞으로
- 2023-09-19 14:09:021358검색
그래프의 지배적 집합은 NP-완전 문제입니다. 이는 부분 집합의 모든 정점 또는 인접한 정점이 부분 집합에 속하도록 정점의 부분 집합입니다. NP의 전체 형태는 다항식 시간에 문제를 확인하는 "비결정적 다항식"입니다. 즉, 솔루션이 올바른지 다항식 시간에 확인할 수 있습니다. 다항식 시간은 선형 검색 시간 복잡도 – n, 이진 검색 – logn, 병합 정렬 - n(log)n 등과 같은 코드에 대해 가장 복잡도가 높습니다. NP-완전 그래프는 합리적인 시간 내에 좋은 솔루션을 제공합니다. 이 애플리케이션은 네트워크 제어, 컴퓨터 실험실의 토폴로지 생성, 소셜 네트워크 및 분산 컴퓨팅과 같은 영역에서 사용됩니다.
노드가 NP 완전 그래프의 지배적인 집합을 가지고 있는지 이해하고 확인해 보겠습니다.
정점은 자신과 이웃을 지배한다고 합니다.
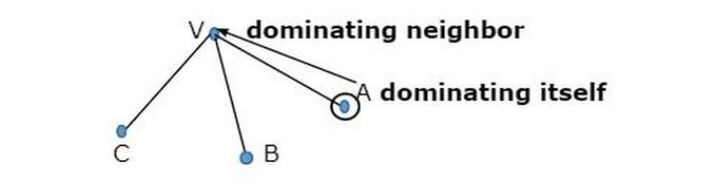
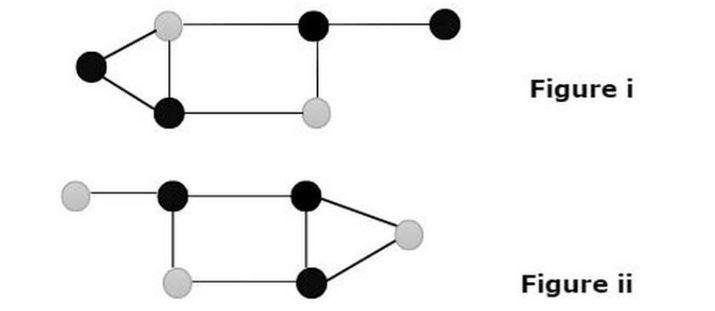
자연계에서 회색이 지배적인 그래프의 노드를 보여주는 두 개의 그래프가 보입니다.
으아아아매개변수
G는 그래프로 간주되고, V는 정점으로 간주되며, E는 가장자리로 간주됩니다.
그래프 G(V, E)와 정수 k가 주어지면 그래프에 크기 k의 지배적인 집합이 있는지 확인하세요. 문제로 지정된 입력은 문제의 인스턴스로 간주됩니다. 그래프 G(V, E)와 정수 k는 그래프 G가 G에서 지배 집합을 가질 수 있는지 묻는 지배 집합 문제의 예입니다. NP-완전 문제의 정의는 NP와 NP-하드 문제 모두인 문제이므로, 문제가 NP-완전임을 증명하는 데는 두 가지 구성 요소가 있습니다 −
Dominator는 NP-완전 문제를 설정합니다
다항식 시간에 X로 감소하는 NP 문제 Y가 있는 경우 X는 NP-완전 문제입니다. NP-완전 문제는 NP 문제만큼 어렵습니다. NP 문제와 NP-Hard 문제의 일부인 경우 문제는 NP-Complete입니다. 비결정론적 튜링 기계는 다항식 시간 내에 NP 완전 문제를 해결할 수 있습니다. 문제가 np-complete이면 np와 np-hard 조합이 모두 있습니다.
이는 np 솔루션의 문제를 다항식 시간에 확인할 수 있음을 의미합니다.
NP 완전의 실제 예에는 -
과 같은 지배적인 집합이 있습니다.의사결정 문제.
그래픽이 일관됩니다.
비결정적 검색 알고리즘
으아아아따라서 이 알고리즘의 전체 시간 복잡도는 O(1)이지만, 이 문제를 해결하는 데 어떤 검색 기술이 더 유용한지는 알 수 없습니다. 이를 비결정적 알고리즘이라고 합니다.
NP-난해한 문제에 지배자가 설정되었습니다
다항식 시간에 문제 X로 환원되는 NP-완전 문제 Y가 존재하는 경우 문제 X는 NP-난해합니다. NP-하드 문제는 NP-완전 문제만큼 어렵습니다. NP-하드 문제가 반드시 NP 범주에 속할 필요는 없습니다.
모든 NP 문제를 다항식 시간 내에 풀 수 있는 경우 이를 NP-Hard라고 합니다. 많은 경우 특정 문제는 다른 문제를 해결하고 줄이기 위해 사용됩니다.
NP-hard의 실제 예에는 -
와 같은 주요 세트가 있습니다.해밀턴 사이클
최적화 문제
최단 경로
결론
우리는 그래프의 주요 집합이 NP-완전이라는 개념을 배웠습니다. 우리는 해밀턴 사이클, 최단 경로 등과 같은 이러한 문제를 연결하는 이산 수학이 얼마나 중요한 측면인지 확인합니다. 프로그래밍 용어에서 NP-완전 문제는 찾기 어렵지만 다항식 시간 내에 해를 직접 확인할 수 있는 문제 클래스입니다.
위 내용은 그래프의 주요 집합이 NP-완전임을 증명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

