Transformer는 학계에서 논의를 촉발한 새로운 이론인 지원 벡터 머신(SVM)입니다.
지난 주말 펜실베이니아 대학과 캘리포니아 리버사이드 대학의 논문에서는 대형 모델을 기반으로 한 Transformer 구조의 원리, Attention 레이어의 최적화된 기하학, 최적의 입력 토큰 분리에 대한 연구를 시도했습니다. 최적이 아닌 토큰은 하드 바운드 SVM 문제 사이에 공식적인 동등성이 설정됩니다.
저자는 hackernews에서 이 이론이 각 입력 시퀀스에서 "좋은" 토큰과 "나쁜" 토큰을 분리하는 SVM 문제를 해결한다고 밝혔습니다. 뛰어난 성능을 갖춘 토큰 선택기로서 이 SVM은 입력에 0-1 레이블을 할당하는 기존 SVM과 본질적으로 다릅니다.
이 이론은 또한 소프트맥스를 통해 주의가 희소성을 유도하는 방법을 설명합니다. SVM 결정 경계의 잘못된 쪽에 있는 "나쁜" 토큰은 소프트맥스 기능에 의해 억제되는 반면 "좋은" 토큰은 그렇지 않은 토큰입니다. 제로 소프트맥스 확률 토큰. 이 SVM이 소프트맥스의 지수 속성에서 파생된다는 점도 언급할 가치가 있습니다.
논문이 arXiv에 올라간 후, 사람들은 다음과 같이 의견을 밝혔습니다. AI 연구의 방향이 정말 나선형으로 돌아가고 있는 걸까요?

한 바퀴를 돌고 난 후에도 지원 벡터 머신은 여전히 구식이 아닙니다.
"Attention is All You Need"라는 고전 논문이 출판된 이후 Transformer 아키텍처는 자연어 처리(NLP) 분야에 혁명적인 발전을 가져왔습니다. Transformer의 주의 계층은 일련의 입력 토큰 X를 받아들이고  를 계산하여 토큰 간의 상관 관계를 평가합니다. 여기서 (K, Q)는 훈련 가능한 키 쿼리 매개변수이며 궁극적으로 원격 종속성을 효과적으로 캡처합니다.
를 계산하여 토큰 간의 상관 관계를 평가합니다. 여기서 (K, Q)는 훈련 가능한 키 쿼리 매개변수이며 궁극적으로 원격 종속성을 효과적으로 캡처합니다.
이제 "Transformers as Support Vector Machines"라는 새 논문에서는 토큰 쌍의 선형 외적을 사용하여 self-attention의 최적화 기하학과 하드 마진 SVM 문제 사이의 형식적 동등성을 확립합니다. 제약 조건은 최적의 입력 토큰을 분리합니다. 최적이 아닌 토큰에서.

문서 링크: https://arxiv.org/pdf/2308.16898.pdf
이 공식 동등성은 Davoud Ataee Tarzanagh et의 "Max-Margin Token Selection in Attention Mechanism" 논문을 기반으로 합니다. al. "Vanishing 정규화를 기반으로 결합된 매개변수의 핵 표준을 최소화하는 SVM 솔루션으로 수렴합니다
. 대조적으로, W를 통해 직접 매개변수화하면 Frobenius 표준 SVM 목표가 최소화됩니다. 이 논문에서는 이러한 수렴을 설명하고 전역 최적이 아닌 지역 최적의 방향으로 발생할 수 있음을 강조합니다.  (2) 이 논문은 또한 적절한 기하학적 조건에서 W 매개변수화 경사하강법의 로컬/글로벌 방향 수렴을 보여줍니다. 중요한 것은 과잉 매개변수화는 SVM 문제의 실현 가능성을 보장하고 고정점 없이 온화한 최적화 환경을 보장함으로써 전역 수렴을 촉진한다는 것입니다.
(2) 이 논문은 또한 적절한 기하학적 조건에서 W 매개변수화 경사하강법의 로컬/글로벌 방향 수렴을 보여줍니다. 중요한 것은 과잉 매개변수화는 SVM 문제의 실현 가능성을 보장하고 고정점 없이 온화한 최적화 환경을 보장함으로써 전역 수렴을 촉진한다는 것입니다.
(3) 이 연구의 이론은 주로 선형 예측 헤드에 적용되지만, 연구팀은 비선형 헤드/MLP가 있는 1층 변압기의 암시적 바이어스를 예측할 수 있는 보다 일반적인 SVM 등가물을 제안합니다.
일반적으로 본 연구의 결과는 일반 데이터 세트에 적용 가능하며 교차 어텐션 레이어로 확장될 수 있으며, 철저한 수치 실험을 통해 연구 결론의 실질적인 타당성을 검증했습니다. 본 연구는 다층 변환기를 최고의 토큰을 분리하고 선택하는 SVM 계층으로 보는 새로운 연구 관점을 확립합니다.
구체적으로, 길이 T의 입력 시퀀스와 임베딩 차원 d
가 주어지면 이 연구에서는 핵심 Cross-Attention 및 Self-Attention 모델을 분석합니다.

여기서 K, Q, V는 각각 학습 가능한 키, 쿼리, 값 행렬입니다.  S(・)는 행별로 적용되는 소프트맥스 비선형성을 나타냅니다
S(・)는 행별로 적용되는 소프트맥스 비선형성을 나타냅니다 . 이 연구에서는 Z의 첫 번째 토큰(z로 표시)이 예측에 사용된다고 가정합니다. 특히 훈련 데이터 세트
. 이 연구에서는 Z의 첫 번째 토큰(z로 표시)이 예측에 사용된다고 가정합니다. 특히 훈련 데이터 세트  ,
,  ,
,  가 주어지면 이 연구에서는 감소 손실 함수
가 주어지면 이 연구에서는 감소 손실 함수  를 사용하여 다음을 최소화합니다. 는 가중치 V 값을 포함하는 예측 헤더. 이 공식에서 모델 f(・)는 Attention 레이어 뒤에 MLP가 오는 단일 레이어 변환기를 정확하게 나타냅니다. 작성자는
를 사용하여 다음을 최소화합니다. 는 가중치 V 값을 포함하는 예측 헤더. 이 공식에서 모델 f(・)는 Attention 레이어 뒤에 MLP가 오는 단일 레이어 변환기를 정확하게 나타냅니다. 작성자는
 를 설정하여 (2)에서 self-attention을 복원합니다. 여기서 x_i는 시퀀스 X_i의 첫 번째 토큰을 나타냅니다. 소프트맥스 연산의 비선형적 특성으로 인해 최적화에 큰 어려움이 따릅니다. 예측 헤드가 고정되고 선형이더라도 문제는 볼록하지 않고 비선형적입니다. 본 연구에서 저자는 주의 가중치(K, Q 또는 W)를 최적화하고 이러한 문제를 극복하여 SVM의 기본 동등성을 확립하는 데 중점을 둡니다.
를 설정하여 (2)에서 self-attention을 복원합니다. 여기서 x_i는 시퀀스 X_i의 첫 번째 토큰을 나타냅니다. 소프트맥스 연산의 비선형적 특성으로 인해 최적화에 큰 어려움이 따릅니다. 예측 헤드가 고정되고 선형이더라도 문제는 볼록하지 않고 비선형적입니다. 본 연구에서 저자는 주의 가중치(K, Q 또는 W)를 최적화하고 이러한 문제를 극복하여 SVM의 기본 동등성을 확립하는 데 중점을 둡니다.
논문의 구조는 다음과 같습니다. 2장에서는 self-attention 및 최적화에 대한 예비 지식을 소개합니다. 3장에서는 self-attention의 최적화 기하학을 분석하여 attention 매개변수 RP가 최대 한계 솔루션에 수렴함을 보여줍니다. 4장과 5장은 각각 전역 및 로컬 경사하강법 분석을 소개하며, 핵심 쿼리 변수 W가 (Att-SVM)의 해로 수렴됨을 보여줍니다. 6장은 비선형 예측 헤드와 일반화된 SVM의 동등성에 대한 결과를 제공합니다. 6 7장은 이론을 순차 및 인과 예측으로 확장합니다. 8장은 관련 문헌을 논의합니다. 마지막으로 9장에서는 열린 질문과 향후 연구 방향을 제시하며 마무리한다. 
 논문의 주요 내용은 다음과 같습니다.
논문의 주요 내용은 다음과 같습니다.
Attention 레이어의 암시적 편향(2-3장)
정규화가 사라질 때 Attention 매개변수(K, Q)를 최적화하면, 방향에서 최대 한계해
로 수렴할 것이며, 핵 표준 목표는 조합 매개변수 입니다. 결합된 매개변수 W를 사용하여 교차 주의를 직접 매개변수화하는 경우 정규화 경로(RP)는 Frobenius 표준을 목표로 하는 (Att-SVM) 솔루션으로 방향적으로 수렴됩니다.
이것은 W와 (K, Q) 파라메트릭 최적화 역학을 공식적으로 구별하여 후자에서 낮은 차수 편향을 드러낸 첫 번째 결과입니다. 본 연구의 이론은 선택된 토큰의 최적성을 명확하게 설명하며 자연스럽게 시퀀스 간 또는 인과 분류 설정으로 확장됩니다. 
 경사하강법의 수렴(4-5장)
경사하강법의 수렴(4-5장)
적절한 초기화 및 선형 수두 h(・)를 사용하면 결합된 키 쿼리 변수 W의 경사하강법(GD) 반복이 다음 방향으로 수렴됩니다. (Att-SVM)의 로컬 최적 솔루션(섹션 5). 로컬 최적을 달성하려면 선택한 토큰이 인접한 토큰보다 높은 점수를 가져야 합니다.
로컬 최적 방향은 반드시 고유한 것은 아니며 문제의 기하학적 특성을 기반으로 결정될 수 있습니다[TLZO23]. 중요한 기여로 저자는 전역 최적을 향한 수렴을 보장하는 기하학적 조건을 식별했습니다(4장). 이러한 조건은 다음과 같습니다:
- 가장 좋은 토큰은 점수에 뚜렷한 차이가 있습니다.
- 초기 그라데이션 방향은 최고의 토큰과 일치합니다.
또한 논문에서는 (1)(Att-SVM) 및 (2) 양성의 타당성을 보장하여 과잉 매개변수화(즉, 차원 d가 크고 동일한 조건)를 보여줍니다. 글로벌 수렴을 촉진하기 위한 최적화 환경(즉, 정지점과 허위 로컬 최적 방향이 없음)(섹션 5.2 참조).
그림 1과 2가 이를 보여줍니다.


SVM 동등의 일반성(6장)
Attention 레이어는 선형 h(・)로 최적화할 때 내재됩니다. 하나의 토큰을 선택하는 편향 각 시퀀스(하드 어텐션이라고도 함). 이는 출력 토큰이 입력 토큰의 볼록 조합인 (Att-SVM)에 반영됩니다. 대조적으로, 저자는 비선형 헤드가 여러 토큰으로 구성되어야 함을 보여줌으로써 변압기 동역학에서의 중요성을 강조합니다(6.1절). 이론에서 얻은 통찰력을 사용하여 저자는 SVM에 대한 보다 일반적이고 동등한 접근 방식을 제안합니다.
특히 그들은 이론에서 다루지 않는 일반적인 경우(예: h(・)는 MLP임) 경사하강법을 통해 훈련된 주의의 암묵적 편향을 우리 방법이 정확하게 예측할 수 있음을 보여줍니다. 특히, 우리의 일반 공식은 주의 가중치를 두 부분으로 분리합니다. SVM에 의해 제어되는 방향 부분은 0-1 마스크를 적용하여 마커를 선택하고, 소프트맥스 확률을 조정하는 유한 부분은 선택된 토큰의 정확한 구성을 결정합니다.
이러한 결과의 중요한 특징은 임의의 데이터 세트(SVM이 가능한 한)에 적용되고 수치적으로 검증될 수 있다는 것입니다. 저자는 변환기의 최대 한계 등가성과 내재적 바이어스를 광범위하게 실험적으로 검증했습니다. 저자는 이러한 발견이 변환기를 계층적 최대 마진 토큰 선택 메커니즘으로 이해하는 데 기여하고 최적화 및 일반화 역학에 대한 향후 연구의 기반을 마련할 수 있다고 믿습니다.
위 내용은 내 말 들어봐, Transformer는 서포트 벡터 머신이야의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM
Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM과학자들은 C. el 그러나 중요한 질문이 발생합니다. 새로운 AI S와 함께 효과적으로 작동하도록 우리 자신의 신경망을 어떻게 조정합니까?
 새로운 Google 유출은 Gemini AI의 구독 변경을 보여줍니다Apr 27, 2025 am 11:08 AM
새로운 Google 유출은 Gemini AI의 구독 변경을 보여줍니다Apr 27, 2025 am 11:08 AMGoogle의 Gemini Advanced : 수평선의 새로운 가입 계층 현재 Gemini Advanced에 액세스하려면 $ 19.99/월 Google One AI Premium Plan이 필요합니다. 그러나 Android Authority 보고서는 다가오는 변경 사항을 암시합니다. 최신 Google p. 내 코드
 데이터 분석 가속이 AI의 숨겨진 병목 현상을 해결하는 방법Apr 27, 2025 am 11:07 AM
데이터 분석 가속이 AI의 숨겨진 병목 현상을 해결하는 방법Apr 27, 2025 am 11:07 AM고급 AI 기능을 둘러싼 과대 광고에도 불구하고 Enterprise AI 배포 내에서 상당한 도전 과제 : 데이터 처리 병목 현상. CEO는 AI 발전을 축하하는 동안 엔지니어는 느린 쿼리 시간, 과부하 파이프 라인,
 Markitdown MCP는 모든 문서를 Markdowns로 변환 할 수 있습니다!Apr 27, 2025 am 09:47 AM
Markitdown MCP는 모든 문서를 Markdowns로 변환 할 수 있습니다!Apr 27, 2025 am 09:47 AM문서 처리는 더 이상 AI 프로젝트에서 파일을 여는 것이 아니라 혼돈을 명확하게 전환하는 것입니다. PDF, PowerPoint 및 Word와 같은 문서는 모든 모양과 크기로 워크 플로우를 범람합니다. 구조화 된 검색
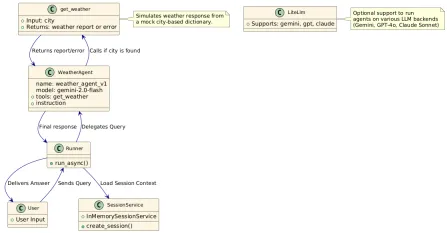 빌딩 에이전트에 Google ADK를 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:42 AM
빌딩 에이전트에 Google ADK를 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:42 AMGoogle의 에이전트 개발 키트 (ADK)의 전력을 활용하여 실제 기능을 갖춘 지능형 에이전트를 만듭니다! 이 튜토리얼은 Gemini 및 GPT와 같은 다양한 언어 모델을 지원하는 ADK를 사용하여 대화 에이전트를 구축하는 것을 안내합니다. w
 효과적인 문제 해결을 위해 LLM을 통해 SLM 사용 - 분석 VidhyaApr 27, 2025 am 09:27 AM
효과적인 문제 해결을 위해 LLM을 통해 SLM 사용 - 분석 VidhyaApr 27, 2025 am 09:27 AM요약: SLM (Small Language Model)은 효율성을 위해 설계되었습니다. 자원 결핍, 실시간 및 개인 정보 보호 환경에서 LLM (Large Language Model)보다 낫습니다. 초점 기반 작업, 특히 도메인 특이성, 제어 성 및 해석 성이 일반적인 지식이나 창의성보다 더 중요합니다. SLM은 LLM을 대체하지는 않지만 정밀, 속도 및 비용 효율성이 중요 할 때 이상적입니다. 기술은 더 적은 자원으로 더 많은 것을 달성하는 데 도움이됩니다. 그것은 항상 운전자가 아니라 프로모터였습니다. 증기 엔진 시대부터 인터넷 버블 시대에 이르기까지 기술의 힘은 문제를 해결하는 데 도움이되는 정도입니다. 인공 지능 (AI) 및보다 최근에 생성 AI가 예외는 아닙니다.
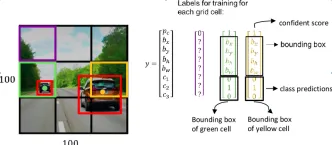 컴퓨터 비전 작업에 Google Gemini 모델을 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:26 AM
컴퓨터 비전 작업에 Google Gemini 모델을 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:26 AM컴퓨터 비전을위한 Google Gemini의 힘을 활용 : 포괄적 인 가이드 주요 AI 챗봇 인 Google Gemini는 강력한 컴퓨터 비전 기능을 포괄하기 위해 대화를 넘어서 기능을 확장합니다. 이 안내서는 사용 방법에 대해 자세히 설명합니다
 Gemini 2.0 Flash vs O4-Mini : Google은 OpenAi보다 더 잘할 수 있습니까?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini : Google은 OpenAi보다 더 잘할 수 있습니까?Apr 27, 2025 am 09:20 AM2025 년의 AI 환경은 Google의 Gemini 2.0 Flash와 Openai의 O4-Mini가 도착하면서 전기가 전환됩니다. 이 최첨단 모델은 몇 주 간격으로 발사되어 비슷한 고급 기능과 인상적인 벤치 마크 점수를 자랑합니다. 이 심층적 인 비교


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

VSCode Windows 64비트 다운로드
Microsoft에서 출시한 강력한 무료 IDE 편집기

SublimeText3 Linux 새 버전
SublimeText3 Linux 최신 버전

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

mPDF
mPDF는 UTF-8로 인코딩된 HTML에서 PDF 파일을 생성할 수 있는 PHP 라이브러리입니다. 원저자인 Ian Back은 자신의 웹 사이트에서 "즉시" PDF 파일을 출력하고 다양한 언어를 처리하기 위해 mPDF를 작성했습니다. HTML2FPDF와 같은 원본 스크립트보다 유니코드 글꼴을 사용할 때 속도가 느리고 더 큰 파일을 생성하지만 CSS 스타일 등을 지원하고 많은 개선 사항이 있습니다. RTL(아랍어, 히브리어), CJK(중국어, 일본어, 한국어)를 포함한 거의 모든 언어를 지원합니다. 중첩된 블록 수준 요소(예: P, DIV)를 지원합니다.






