숫자맞추기 게임?
- PHPz앞으로
- 2023-09-16 10:53:011391검색
Number Connect는 그리드에서 숫자를 연결하는 경로를 찾는 논리 퍼즐입니다.
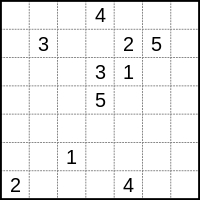
Numberlink 퍼즐의 간단한 예 Numberlink 퍼즐에 대한 솔루션
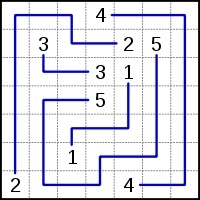
Rules - 플레이어는 그리드에서 일치하는 모든 숫자를 하나의 연속 선(또는 경로)으로 일치시켜야 합니다. 선은 갈라지거나 교차할 수 없으며 숫자는 각 선의 끝에 있어야 합니다(즉, 중간이 아님). 일부 Numberlink 디자이너는 이를 지정하지 않지만 고유한 솔루션이 있고 그리드의 모든 셀이 채워지는 경우에만 문제가 잘 설계된 것으로 간주됩니다.
Game - n×n 정사각형 배열을 생각해 보세요. 일부 사각형은 비어 있고 일부는 단색이며 일부 비단층 사각형은 정수 1, 2, 3,...으로 표시됩니다. 각 정수는 보드에서 서로 다른 두 개의 사각형을 차지합니다. 플레이어의 임무는 수평 및 수직 이동만을 사용하여 간단한 경로를 통해 보드에 있는 각 정수의 두 발생을 연결하는 것입니다. 서로 다른 두 경로는 교차할 수 없습니다. 어떤 경로에도 고체 블록이 포함될 수 없습니다. 어떤 경로에도 고체 블록이 허용되지 않습니다. 마지막으로, 모든 비고체 사각형은 경로로 채워져야 합니다.
알고리즘 - 보드 크기 n×n이 주어지면 효율적인 무작위 퍼즐을 준비하기 위해 먼저 보드에 무작위 단순 분리 경로를 생성합니다. 생성된 모든 경로 외부에 여러 개의 격리된 블록이 남아 있는 경우 이러한 격리된 블록을 솔리드(금지됨)로 표시합니다. 그런 다음 경로의 끝점과 단색 사각형 목록을 퍼즐로 사용합니다.
그래서 먼저 솔루션을 생성한 다음 솔루션에서 퍼즐을 해결합니다. 경로와 단색 사각형은 n×n 체스판을 여러 부분으로 나눕니다. 우리는 이 분할을 생성하기 위해 Union-Lookup 데이터 구조를 사용합니다. 데이터 구조는 체스판에서 n^2 정사각형의 하위 집합을 처리합니다.
Explanation
체스판에서 (a) (i, j)와 (k, l)이 서로 이웃하고 (b)와 같은 사각형 (i, j)와 (k, l)을 무작위로 찾습니다. ) (i, j)나 (k, l) 모두 지금까지 생성된 경로에 속하지 않습니다. 전체 보드에서 그러한 사각형 쌍이 발견되지 않으면 실패가 반환됩니다. /* 여기서 (i, j)와 (k, l)은 구성될 새 경로의 처음 두 사각형입니다. *
(i, j)와 (k, l)을 포함하는 두 개의 결합 찾기 트리를 병합합니다.
현재 경로를 확장할 수 없을 때까지 다음 단계를 반복합니다. (i, j)의 이름을 (k, l)로 바꿉니다. (a) (k, l)이 지금까지 생성된 경로(현재 경로 포함)에 속하지 않도록 (i, j)의 이웃 사각형(k, l)을 무작위로 찾습니다. (b) 구성된 현재 경로에서 부분적으로( i, j)의 유일한 이웃은 (k, l)입니다.
그러한 이웃 사각형 (k, l)이 발견되지 않으면 경로를 더 이상 확장할 수 없으므로 루프가 끊어집니다.
그렇지 않으면 (i, j)와 (k를 포함하는 두 개의 합집합 , l)은 검색 세트 트리 병합이 됩니다.
새 경로의 시작 블록과 끝 블록의 플래그를 설정합니다.
반환 성공
Input
| || || || || || || 4 | | || || || || || 3 || | | || || 2 || 2 || || || 3 | | || || || || X || || 1 | | || || 6 || || || 7 || 7 | | 5 || 4 || || X || || X || 1 | | || 5 || || 6 || || || |
Output
위 표의 솔루션
| 4 || 4 || 4 || 4 || 4 || 4 || 4 | | 4 || 1 || 1 || 1 || 1 || 3 || 3 | | 4 || 1 || 2 || 2 || 1 || 1 || 3 | | 4 || 1 || 1 || 1 || X || 1 || 1 | | 4 || 4 || 6 || 1 || 1 || 7 || 7 | | 5 || 4 || 6 || X || 1 || X || 1 | | 5 || 5 || 6 || 6 || 1 || 1 || 1 |
예
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
struct _node *parent;
int rank;
int path_number;
int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
int i, j;
for (i=0;i<n;i++){
for (j=0;j<n;j++){
node *np;
np = (node *)malloc(sizeof(node));
np->rank = 0;
np->parent = NULL;
np->path_number = 0;
np->endpoint = 0;
arr[i][j] = np;
}
}
}
/*
Input:a node Output:the set pointer of the set the node belongs to
설명 - 노드를 가져오고 세트 포인터를 반환합니다. . */
node *findset(node *n) {
if (n->parent != NULL)
n = n->parent;
return n;
}
void setunion(node *x, node *y) {
x = findset(x);
y = findset(y);
if (x->rank > y->rank)
y->parent = x;
else {
x->parent = y;
if(x->rank == y->rank)
y->rank++;
}
}
int neighbour(int n, node ***arr) {
int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
int k = rand()%(n*n);
while (ct < (n*n)) {
k %= (n*n);
i1 = k/n;
j1 = k%n;
if (arr[i1][j1]->path_number==0) {
int kk = rand()%4;
int cc = 0;
switch (kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 4: if(cc==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 5: if(cc==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 6: if(cc==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 7: if(cc==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
}
}
if(flag==1)
break;
ct++;
k++;
}
if(ct<n*n) {
k2= (i2*n)+j2;
return k*(n*n)+k2;
} else {
return -1;
}
}
int checkneigh(int k1, int k2, int n, node ***arr) {
int i= k2/n;
int j= k2%n;
int ii= k1/n;
int jj= k1%n;
int ct=0;
if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
ct++;
if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
ct++;
if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
ct++;
if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
ct++;
if(ct>1)
return 0;
else
return 1;
}
int valid_next(int k, int n, node ***arr) {
int i1, i2, j1, j2, a, b, kk, stat,ct=0;
int flag=0;
i1= k/n;
j1= k%n;
kk= rand()%4;
switch(kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 4: if(ct==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 5: if(ct==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 6: if(ct==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 7: if(ct==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d</p><p>",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
}
//printf("flag- %d</p><p>",flag);
if(flag==0)
return -1;
if(flag) {
//printf("value sent- %d</p><p>", i2*n + j2);
return (i2*n)+j2;
}
}
int addpath(node ***arr, int n, int ptno) {
int a,b,k1,k2;
int i1,j1,i2,j2;
k2= neighbour( n, arr);
if(k2==-1) //no valid pair found to start with
return 0;
k1= k2/(n*n);
k2= k2%(n*n);
//printf("%d %d</p><p>",k1,k2);
i1= k1/n;
j1= k1%n;
i2= k2/n;
j2= k2%n;
arr[i1][j1]->endpoint= 1;
arr[i2][j2]->path_number= ptno;
arr[i1][j1]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1, n2);
while(1) {
i1= i2;
j1= j2;
k1= (i1*n)+j1;
k2= valid_next(k1,n,arr);
if(k2==-1) {
arr[i1][j1]->endpoint= 1;
break;
}
i2=k2/n;
j2=k2%n;
arr[i2][j2]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1,n2);
}
return 1;
}
void printtable(node ***arr, int n) {
int i,j;
printf("Table to be solved:</p><p>");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->endpoint ==1){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else if(arr[i][j]->path_number==0)
printf("| X |");
else
printf("| |");
}
printf("</p><p>");
}
printf("</p><p></p><p>The solution to the above table:</p><p>");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->path_number != 0){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else
printf("| X |");
}
printf("</p><p>");
}
}
int main(void) {
srand((unsigned int) time (NULL));
int i, j;
int ct = 1;
int n = 7;
node*** pointers= (node ***)malloc(n*sizeof(node **));
for (i=0; i<n; i++)
pointers[i] = (node **)malloc(n*sizeof(node *));
initboard(pointers, n);
while(1) {
i = addpath(pointers, n, ct);
if (i==0) {
break;
} else {
ct++;
}
}
printtable(pointers,n);
return 0;
}위 내용은 숫자맞추기 게임?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
성명：
이 기사는 tutorialspoint.com에서 복제됩니다. 침해가 있는 경우 admin@php.cn으로 문의하시기 바랍니다. 삭제
이전 기사：C 언어의 다양한 데이터 유형은 무엇입니까?다음 기사：C 언어의 다양한 데이터 유형은 무엇입니까?