C++를 사용하여 N-진 트리를 탐색하는 방법의 수 찾기

N-ary 트리가 주어지면 우리의 임무는 트리를 탐색하는 총 방법 수를 찾는 것입니다. 예: −

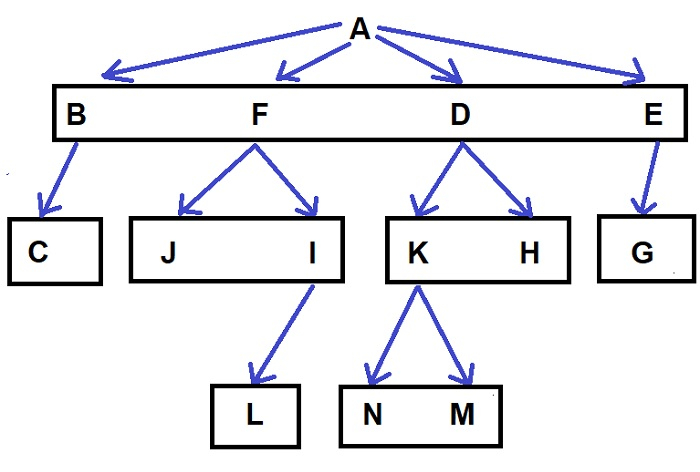
위 트리의 경우 출력은 192입니다.

이 문제를 풀려면 조합론에 대한 지식이 필요합니다. 이제 이 문제에서 우리는 각 경로의 가능한 모든 조합을 확인하면 되며 이것이 답을 줄 것입니다.

해를 ​​찾는 방법

이 방법에서는 레벨 순회를 수행하고 각 노드의 자식 수를 확인한 다음 답에 계승 곱하면 됩니다.

Example

위 메서드의 C++ 코드

#include<bits/stdc++.h>
using namespace std;
struct Node{ // structure of our node
    char key;
    vector<Node *> child;
};
Node *createNode(int key){ // function to initialize a new node
    Node *temp = new Node;
    temp->key = key;
    return temp;
}
long long fact(int n){
    if(n <= 1)
        return 1;
    return n * fact(n-1);
}
int main(){
    Node *root = createNode(&#39;A&#39;);
    (root->child).push_back(createNode(&#39;B&#39;));
    (root->child).push_back(createNode(&#39;F&#39;));
    (root->child).push_back(createNode(&#39;D&#39;));
    (root->child).push_back(createNode(&#39;E&#39;));
    (root->child[2]->child).push_back(createNode(&#39;K&#39;));
    (root->child[1]->child).push_back(createNode(&#39;J&#39;));
    (root->child[3]->child).push_back(createNode(&#39;G&#39;));
    (root->child[0]->child).push_back(createNode(&#39;C&#39;));
    (root->child[2]->child).push_back(createNode(&#39;H&#39;));
    (root->child[1]->child).push_back(createNode(&#39;I&#39;));
    (root->child[2]->child[0]->child).push_back(createNode(&#39;N&#39;));
    (root->child[2]->child[0]->child).push_back(createNode(&#39;M&#39;));
    (root->child[1]->child[1]->child).push_back(createNode(&#39;L&#39;));
    queue<Node*> q;
    q.push(root);
    long long ans = 1;
    while(!q.empty()){
        auto z = q.front();
        q.pop();
        ans *= fact(z -> child.size());
        cout << z->child.size() << " ";
        for(auto x : z -> child)
           q.push(x);
   }
   cout << ans << "\n";
   return 0;
}

Output

4 1 2 2 1 0 0 1 2 0 0 0 0 0 192

위 코드 설명

이 메서드에서는 BFS(Breadth First Search) 또는 계층적 순회를 적용하고 각 노드의 자식을 확인합니다. 노드. 그런 다음 해당 수량의 계승값에 우리의 답을 곱합니다.

결론

이 튜토리얼에서는 N-ary 트리 조합을 탐색하고 BFS를 적용하는 여러 가지 방법을 소개했습니다. 우리는 또한 이 문제를 해결하기 위한 C++ 프로그램과 완전한 방법을 배웠습니다.

C, Java, Python 및 기타 언어와 같은 다른 언어로 동일한 프로그램을 작성할 수 있습니다. 이 튜토리얼이 도움이 되었기를 바랍니다.

위 내용은 C++를 사용하여 N-진 트리를 탐색하는 방법의 수 찾기의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!