Python을 사용한 회귀 분석 및 최적 직선
- 王林앞으로
- 2023-08-28 09:33:051628검색
이 튜토리얼에서는 Python 프로그래밍을 사용하여 회귀 분석과 최적선을 구현합니다
소개
회귀분석은 예측분석의 가장 기본적인 형태입니다.
통계에서 선형 회귀는 스칼라 값과 하나 이상의 설명 변수 간의 관계를 모델링하는 방법입니다.
기계 학습에서 선형 회귀는 지도 알고리즘입니다. 이 알고리즘은 독립변수를 기반으로 목표값을 예측합니다.
선형 회귀 및 회귀 분석에 대한 추가 정보
선형 회귀/분석에서 대상은 급여, BMI 등과 같은 실제 또는 연속 값입니다. 이는 종속변수와 독립변수 집합 간의 관계를 예측하는 데 자주 사용됩니다. 이러한 모델은 일반적으로 선형 방정식에 적합하지만 고차 다항식을 포함한 다른 유형의 회귀가 있습니다.
선형 모델을 데이터에 피팅하기 전에 데이터 포인트 간에 선형 관계가 있는지 확인해야 합니다. 이는 산점도에서 분명합니다. 알고리즘/모델의 목표는 가장 적합한 선을 찾는 것입니다.
이 기사에서는 C++를 사용한 선형 회귀 분석 및 구현을 살펴보겠습니다.
선형 회귀 방정식은 Y = c + mx 형식입니다. 여기서 Y는 대상 변수이고 X는 독립 변수 또는 설명 매개변수/변수입니다. m은 회귀선의 기울기이고 c는 절편입니다. 이는 2D 회귀 작업이므로 모델은 훈련 중에 가장 적합한 선을 찾으려고 합니다. 모든 점이 정확히 같은 선에 정렬될 필요는 없습니다. 일부 데이터 포인트는 선 위에 있을 수 있고, 일부는 선 전체에 흩어져 있을 수 있습니다. 선과 데이터 점 사이의 수직 거리는 잔차입니다. 값은 점이 선 아래에 있는지 위에 있는지에 따라 음수 또는 양수일 수 있습니다. 잔차는 선이 데이터에 얼마나 잘 맞는지를 나타내는 척도입니다. 알고리즘은 총 잔차를 최소화하기 위해 연속적입니다.
각 관측치의 잔차는 예측된 y값(종속변수)과 관측된 y값의 차이입니다
$$mathrm{잔차: =: 실제: y: 값:−:예측: y: 값}$$
$$mathrm{ri:=:yi:−:y'i}$$
선형 회귀 모델의 성능을 평가하는 가장 일반적인 측정 기준은 제곱 평균 오차(RMSE)입니다. 기본 아이디어는 모델의 예측이 실제 관찰과 비교하여 얼마나 나쁜지/잘못된지를 측정하는 것입니다.
그러므로 RMSE가 높으면 '나쁨'이고 RMSE가 낮으면 '좋음'입니다
RMSE 오류는
$$mathrm{RMSE:=:sqrt{frac{sum_i^n=1:(this:-:this')^2}{n}}}$$ p>
RMSE는 모든 잔차의 평균 제곱근입니다.
Python을 사용하여 구현
예
으아아아출력
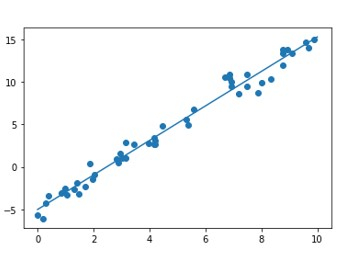
결론
회귀 분석은 기계 학습 및 통계의 예측 분석에 사용되는 매우 간단하면서도 강력한 기술입니다. 아이디어는 단순성과 독립 변수와 목표 변수 간의 기본 선형 관계에 있습니다.
위 내용은 Python을 사용한 회귀 분석 및 최적 직선의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

