대형 모델 등장에서 가장 미스터리한 현상 중 하나는 CoT(Chain of Thought Tips)로, 이는 수학적 추론과 의사결정 문제를 해결하는 데 놀라운 결과를 보여주었습니다. CoT는 얼마나 중요합니까? 성공의 메커니즘은 무엇입니까? 이 기사에서 Peking University의 여러 연구자들은 CoT가 LLM(대형 언어 모델) 추론을 실현하는 데 없어서는 안 될 필수 요소임을 입증하고 CoT가 이론 및 실험적 관점에서 LLM의 엄청난 잠재력을 어떻게 발휘할 수 있는지 보여줍니다.
최근 연구에 따르면 CoT(사고 사슬 프롬프트)는 LLM(대형 언어 모델)의 성능을 크게 향상할 수 있으며 특히 수학과 추론과 관련된 복잡한 작업을 처리하는 데 적합합니다. 그러나 많은 성공에도 불구하고 CoT의 메커니즘과 LLM의 잠재력을 활용하는 방법은 여전히 파악하기 어렵습니다.
최근 북경대학교의 새로운 연구에서는 이론적 관점에서 CoT의 숨겨진 미스터리를 밝혀냈습니다.

논문 링크: https://arxiv.org/abs/2305.15408
Transformer 기반의 대형 언어 모델은 자연어 처리, 다양한 작업에서 보편적인 모델이 되었습니다. 널리 사용되었습니다. 주류 대형 모델은 일반적으로 자기회귀 패러다임을 기반으로 구현됩니다. 특히 다양한 작업(예: 텍스트 번역, 텍스트 생성, 질문 답변 등)은 질문의 입력과 설명이 시퀀스 생성 문제로 일률적으로 간주될 수 있습니다. 질문의 답변은 프롬프트(프롬프트)라고 불리는 단어(토큰) 시퀀스로 함께 인코딩됩니다. 질문에 대한 답변은 프롬프트를 기반으로 조건부로 후속 단어를 생성하는 작업으로 변환될 수 있습니다.

대형 모델 분야의 많은 연구에 따르면 잘 디자인된 프롬프트 단어가 모델 성능에 중요한 역할을 하는 것으로 나타났습니다. 특히 산술 또는 추론 관련 작업의 경우 CoT는 생성된 답변의 정확성을 크게 향상시키는 것으로 나타났습니다. 아래 그림에서 볼 수 있듯이 수학적 추론이 필요한 작업의 경우 대형 모델에서 직접 생성된 답변이 잘못된 경우가 많습니다(아래 그림 a,b). 그러나 대형 모델이 전체 사고 사슬(중간 도출 단계)을 출력하도록 프롬프트를 수정하면 결국 정답을 얻을 수 있게 됩니다(아래 c, d).

실제로 사고 사슬 프롬프트를 구현하는 두 가지 주요 방법이 있습니다. 하나는 프롬프트에 "단계적으로 생각해보자"와 같은 특정 문구를 추가하여 이를 트리거하는 것입니다(그림 참조). 다른 하나는 사고 사슬 시연의 소수의 예를 제공하여 대규모 모델이 해당 파생 프로세스를 시뮬레이션할 수 있도록 하는 것입니다(위의 그림 d 참조).
그러나 CoT는 수많은 실험에서 놀라운 성능을 달성했지만 그 뒤에 있는 이론적 메커니즘은 여전히 미스터리로 남아 있습니다. 한편으로, 대형 모델은 실제로 수학, 추론 등에 관한 질문에 직접 답하는 데 본질적인 이론적 결함을 가지고 있습니까? 반면에 CoT가 이러한 작업에 대한 대형 모델의 기능을 향상시킬 수 있는 이유는 무엇입니까? 본 논문은 이론적 관점에서 위의 질문에 답한다.
구체적으로 연구자들은 CoT를 모델 표현 능력의 관점에서 연구합니다. 수학적 작업과 일반적인 의사 결정 작업에 대해 이 기사에서는 다음 두 가지 측면에서 자동 회귀 기반 Transformer 모델의 표현 능력을 연구합니다. (1) 생성 (2) CoT를 사용하여 완전한 솔루션 단계를 생성합니다.
CoT는 수학 문제를 해결하는 열쇠입니다
GPT-4로 대표되는 대형 모델은 충격적인 수학적 능력을 보여주었습니다. 예를 들어 대부분의 고등학교 수학 문제를 정확하게 풀 수 있으며 심지어 수학자들의 연구 조교가 되기도 했습니다.
대형 모델의 수학적 기능을 연구하기 위해 이 기사에서는 매우 기본이지만 핵심적인 두 가지 수학 작업인 산술과 방정식을 선택했습니다(다음 그림은 이 두 작업의 입력 및 출력 예를 제공합니다). 이는 복잡한 수학 문제를 해결하기 위한 기본 구성 요소이므로 이 두 가지 핵심 수학 문제를 연구함으로써 일반적인 수학 문제에 대한 대형 모델의 기능을 더 깊이 이해할 수 있습니다.

연구원들은 먼저 Transformer가 중간 단계를 출력하지 않고 위 질문에 대한 답변을 출력할 수 있는지 여부를 조사했습니다. 그들은 현실과 매우 일치하는 가정, 즉 로그 정밀도 변환기를 고려했습니다. 즉, 변환기의 각 뉴런은 제한된 정밀도의 부동 소수점 수만 나타낼 수 있습니다(정밀도는 log n 비트). 여기서 n은 최대 길이입니다. 문장의. 이 가정은 현실과 매우 유사합니다. 예를 들어 GPT-3에서는 기계 정밀도(16 또는 32비트)가 일반적으로 최대 출력 문장 길이(2048)보다 훨씬 작습니다.
이러한 가정 하에서 연구자들은 핵심적으로 불가능한 결과를 증명했습니다. 상수 레이어와 너비 d를 갖는 자동 회귀 Transformer 모델의 경우, 답을 직접 출력하여 위의 두 가지 수학적 문제를 풀 때 매우 필요합니다. 대형 모델 너비 d. 구체적으로 d는 입력 길이 n이 커짐에 따라 다항식보다 커져야 합니다.
이 결과가 나온 근본적인 이유는 위의 두 가지 문제에 대해 효율적인 병렬 알고리즘이 없어 일반적인 병렬 모델인 Transformer가 이를 해결할 수 없기 때문입니다. 이 기사에서는 이론적인 컴퓨터 과학의 회로 복잡도 이론을 사용하여 위의 정리를 엄격하게 증명했습니다.
그럼, 모델이 직접 답을 출력하는 것이 아니라, 중간 도출 단계를 위 그림과 같은 형태로 출력한다면 어떨까요? 연구자들은 모델이 중간 단계를 출력할 수 있을 때 고정 크기(입력 길이 n에 의존하지 않음) 자동 회귀 변환기 모델이 위의 두 가지 수학적 문제를 해결할 수 있다는 것을 구성을 통해 추가로 입증했습니다. 이전 결과를 비교해 보면 CoT를 추가하면 대형 모델의 표현력이 크게 향상되는 것을 알 수 있습니다. 연구원들은 이에 대해 직관적으로 이해했습니다. 이는 CoT의 도입으로 생성된 출력 단어가 입력 레이어에 지속적으로 피드백되어 모델의 유효 깊이가 크게 증가하여 CoT의 출력 길이에 비례하기 때문입니다. 따라서 Transformer의 병렬 복잡성이 크게 향상됩니다.
CoT는 일반적인 의사결정 문제를 해결하는 열쇠입니다
연구원들은 수학적 문제 외에도 CoT의 일반적인 작업 해결 능력을 더욱 고려했습니다. 그들은 의사결정 문제부터 시작하여 동적 프로그래밍이라고 불리는 의사결정 문제를 해결하기 위한 일반적인 프레임워크를 고려했습니다.동적 프로그래밍(DP)의 기본 아이디어는 복잡한 문제를 순차적으로 해결할 수 있는 일련의 소규모 하위 문제로 분해하는 것입니다. 문제를 분해하면 다양한 하위 문제 사이에 상당한 상호 관계(중복)가 존재하므로 각 하위 문제는 이전 하위 문제에 대한 답을 사용하여 효율적으로 해결할 수 있습니다.
최장 오름차순 하위 시퀀스(LIS)와 편집 거리 해결(ED)은 "알고리즘 소개" 책에서 제안된 두 가지 유명한 DP 문제입니다. 다음 표에는 이 두 가지 문제의 상태 공간과 전환이 나열되어 있습니다. 기능의.

연구원들은 자동 회귀 Transformer 모델이 하위 문제를 해결하는 순서대로 완전한 동적 프로그래밍 사고 체인을 출력할 수 있으므로 다음으로 해결 가능한 모든 작업에 대해 출력할 수 있음을 입증했습니다. 동적 프로그래밍 정답입니다. 마찬가지로 연구자들은 생성적 사고 체인이 필요하다는 점을 추가로 입증했습니다. 많은 어려운 동적 프로그래밍 문제의 경우 상수 계층, 다항식 크기의 Transformer 모델은 정답을 직접 출력할 수 없습니다. 이 기사는 문맥 자유 문법 멤버십 테스트 문제에 대한 반례를 제공합니다.
실험연구원들은 산술 표현식 평가, 선형 방정식 풀기, 가장 긴 오름차순 부분 수열 풀기, 편집 거리 풀기 등 네 가지 작업을 고려하여 위의 이론을 검증하기 위해 마침내 수많은 실험을 설계했습니다.실험 결과에 따르면 CoT 데이터를 사용하여 훈련했을 때 3계층 자동 회귀 Transformer 모델이 모든 작업에서 거의 완벽한 성능을 달성할 수 있었던 것으로 나타났습니다. 그러나 정답을 직접 출력하는 것은 모든 작업에서 제대로 수행되지 않습니다(더 깊은 모델에서도). 이 결과는 다양한 복잡한 작업을 해결하는 Autoregressive Transformer의 능력을 명확하게 보여주고 이러한 작업을 해결하는 데 CoT의 중요성을 보여줍니다.


위 내용은 사고 체인은 언어 모델의 숨겨진 기능을 어떻게 해제합니까? 최신 이론적 연구는 그 뒤에 숨은 미스터리를 밝혀줍니다의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 AI 내부 배포의 숨겨진 위험 : 거버넌스 격차 및 치명적인 위험Apr 28, 2025 am 11:12 AM
AI 내부 배포의 숨겨진 위험 : 거버넌스 격차 및 치명적인 위험Apr 28, 2025 am 11:12 AMApollo Research의 새로운 보고서에 따르면 고급 AI 시스템의 점검되지 않은 내부 배치는 상당한 위험을 초래합니다. 주요 AI 기업들 사이에서 널리 퍼져있는 이러한 감독 부족은 uncont에서 범위에 이르는 잠재적 인 치명적인 결과를 허용합니다.
 AI Polygraph 구축Apr 28, 2025 am 11:11 AM
AI Polygraph 구축Apr 28, 2025 am 11:11 AM전통적인 거짓말 탐지기는 구식입니다. 손목 대역으로 연결된 포인터에 의존하는 것은 대상의 활력 징후와 물리적 반응을 인쇄하는 거짓말 탐지기가 거짓말을 식별하는 데 정확하지 않습니다. 그렇기 때문에 거짓말 탐지 결과는 일반적으로 법원에서 채택되지는 않지만 많은 무고한 사람들이 감옥에 갇히게되었습니다. 대조적으로, 인공 지능은 강력한 데이터 엔진이며, 작동 원리는 모든 측면을 관찰하는 것입니다. 이것은 과학자들이 다양한 방식으로 진실을 찾는 응용 분야에 인공 지능을 적용 할 수 있음을 의미합니다. 한 가지 방법은 거짓말 탐지기처럼 심문을받는 사람의 중요한 부호 반응을 분석하지만보다 상세하고 정확한 비교 분석을 분석하는 것입니다. 또 다른 방법은 언어 마크 업을 사용하여 사람들이 실제로 말하는 것을 분석하고 논리와 추론을 사용하는 것입니다. 말이 갈 때, 한 거짓말은 또 다른 거짓말을 번식시키고 결국
 항공 우주 산업에서 AI가 이륙을 위해 청산 되었습니까?Apr 28, 2025 am 11:10 AM
항공 우주 산업에서 AI가 이륙을 위해 청산 되었습니까?Apr 28, 2025 am 11:10 AM혁신의 선구자 인 항공 우주 산업은 AI를 활용하여 가장 복잡한 도전을 해결하고 있습니다. Modern Aviation의 복잡성 증가는 AI의 자동화 및 실시간 인텔리전스 기능이 필요합니다.
 베이징의 봄 로봇 레이스를보고 있습니다Apr 28, 2025 am 11:09 AM
베이징의 봄 로봇 레이스를보고 있습니다Apr 28, 2025 am 11:09 AM로봇 공학의 빠른 발전은 우리에게 매혹적인 사례 연구를 가져 왔습니다. Noetix의 N2 로봇의 무게는 40 파운드가 넘고 키가 3 피트이며 백 플립을 할 수 있다고합니다. Unitree의 G1 로봇의 무게는 N2 크기의 약 2 배이며 키는 약 4 피트입니다. 경쟁에 참여하는 작은 휴머노이드 로봇도 많으며 팬이 앞으로 나아가는 로봇도 있습니다. 데이터 해석 하프 마라톤은 12,000 명 이상의 관중을 끌어 들였지만 21 명의 휴머노이드 로봇 만 참여했습니다. 정부는 참여 로봇이 경쟁 전에 "집중 훈련"을 수행했다고 지적했지만 모든 로봇이 전체 경쟁을 완료 한 것은 아닙니다. 챔피언 -Tiangong Ult Beijing Humanoid Robot Innovation Center가 개발했습니다.
 거울 함정 : AI 윤리와 인간 상상력의 붕괴Apr 28, 2025 am 11:08 AM
거울 함정 : AI 윤리와 인간 상상력의 붕괴Apr 28, 2025 am 11:08 AM인공 지능은 현재 형태로 진정으로 지능적이지 않습니다. 기존 데이터를 모방하고 정제하는 데 능숙합니다. 우리는 인공 지능을 만들지 않고 오히려 인공적인 추론을 만들고 있습니다.
 새로운 Google Leak은 Handy Google 사진 기능 업데이트가 공개됩니다Apr 28, 2025 am 11:07 AM
새로운 Google Leak은 Handy Google 사진 기능 업데이트가 공개됩니다Apr 28, 2025 am 11:07 AM보고서에 따르면 Google Photos Android 버전 7.26 코드에 업데이트 된 인터페이스가 숨겨져 있으며 사진을 볼 때마다 새로 감지 된 얼굴 썸네일 행이 화면 하단에 표시됩니다. 새로운 얼굴 썸네일에는 이름 태그가 없으므로 탐지 된 각 사람에 대한 자세한 정보를 보려면 개별적으로 클릭해야한다고 생각합니다. 현재이 기능은 Google 사진이 이미지에서 찾은 사람들 외에는 정보를 제공하지 않습니다. 이 기능은 아직 사용할 수 없으므로 Google이 어떻게 정확하게 사용할 것인지 모릅니다. Google은 썸네일을 사용하여 선택된 사람들의 더 많은 사진을 찾는 속도를 높이거나 편집 할 개인을 선택하는 것과 같은 다른 목적으로 사용될 수 있습니다. 기다렸다가 보자. 지금은
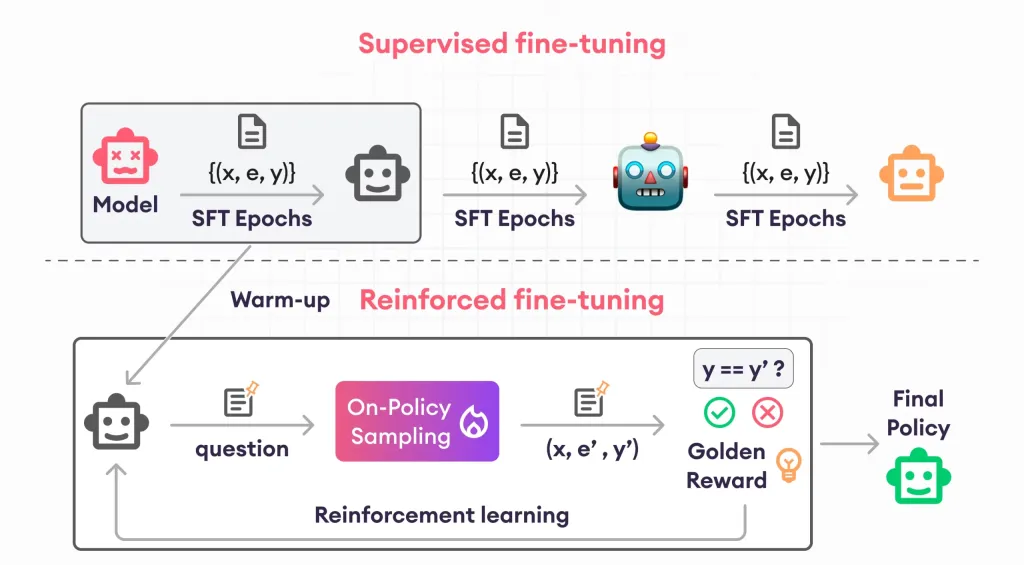 강화 조정 안내서 - 분석 VidhyaApr 28, 2025 am 09:30 AM
강화 조정 안내서 - 분석 VidhyaApr 28, 2025 am 09:30 AM강화 결합은 인간의 피드백을 기반으로 조정하도록 모델을 가르치면서 AI 개발을 흔들었다. 감독 학습 기초가 보상 기반 업데이트와 혼합되어 더 안전하고 정확하며 진정으로 도움을줍니다.
 Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM
Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM과학자들은 C. el 그러나 중요한 질문이 발생합니다. 새로운 AI S와 함께 효과적으로 작동하도록 우리 자신의 신경망을 어떻게 조정합니까?


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

에디트플러스 중국어 크랙 버전
작은 크기, 구문 강조, 코드 프롬프트 기능을 지원하지 않음

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

MinGW - Windows용 미니멀리스트 GNU
이 프로젝트는 osdn.net/projects/mingw로 마이그레이션되는 중입니다. 계속해서 그곳에서 우리를 팔로우할 수 있습니다. MinGW: GCC(GNU Compiler Collection)의 기본 Windows 포트로, 기본 Windows 애플리케이션을 구축하기 위한 무료 배포 가능 가져오기 라이브러리 및 헤더 파일로 C99 기능을 지원하는 MSVC 런타임에 대한 확장이 포함되어 있습니다. 모든 MinGW 소프트웨어는 64비트 Windows 플랫폼에서 실행될 수 있습니다.

mPDF
mPDF는 UTF-8로 인코딩된 HTML에서 PDF 파일을 생성할 수 있는 PHP 라이브러리입니다. 원저자인 Ian Back은 자신의 웹 사이트에서 "즉시" PDF 파일을 출력하고 다양한 언어를 처리하기 위해 mPDF를 작성했습니다. HTML2FPDF와 같은 원본 스크립트보다 유니코드 글꼴을 사용할 때 속도가 느리고 더 큰 파일을 생성하지만 CSS 스타일 등을 지원하고 많은 개선 사항이 있습니다. RTL(아랍어, 히브리어), CJK(중국어, 일본어, 한국어)를 포함한 거의 모든 언어를 지원합니다. 중첩된 블록 수준 요소(예: P, DIV)를 지원합니다.

DVWA
DVWA(Damn Vulnerable Web App)는 매우 취약한 PHP/MySQL 웹 애플리케이션입니다. 주요 목표는 보안 전문가가 법적 환경에서 자신의 기술과 도구를 테스트하고, 웹 개발자가 웹 응용 프로그램 보안 프로세스를 더 잘 이해할 수 있도록 돕고, 교사/학생이 교실 환경 웹 응용 프로그램에서 가르치고 배울 수 있도록 돕는 것입니다. 보안. DVWA의 목표는 다양한 난이도의 간단하고 간단한 인터페이스를 통해 가장 일반적인 웹 취약점 중 일부를 연습하는 것입니다. 이 소프트웨어는







