Java에서 토폴로지 정렬을 구현하는 방법

준비

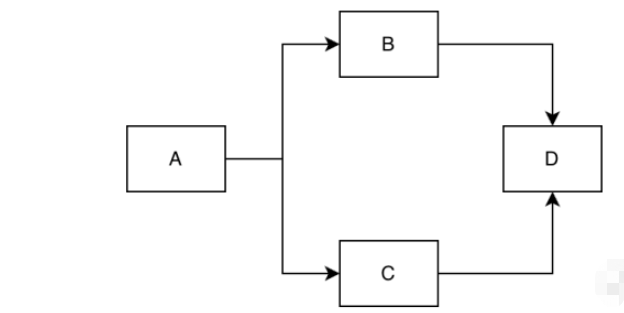
이 섹션에서는 유향 그래프와 관련된 알고리즘을 소개하므로 먼저 유향 그래프의 일부 개념을 설명하겠습니다. 이후 기사에서는 이러한 개념을 자세히 설명하지 않습니다. 먼저 유향 그래프의 노드는 화살표가 있는 선으로 연결됩니다. 노드의 아웃 차수와 인 차수를 사용하여 연결 끝이 노드를 가리킬 때 아웃 차수는 1만큼 증가하고 연결 화살표가 노드를 가리킬 때, 그 차수는 1씩 증가합니다. 다음 예를 살펴보세요. A의 진입 차수는 0, 진출 차수는 2이고, B의 진입 차수는 1, 진출 차수는 1이며, C의 진입 차수는 1, 진출 차수는 1입니다. D의 차수는 1이고, D의 진입 차수는 2이고, 외차는 0입니다.

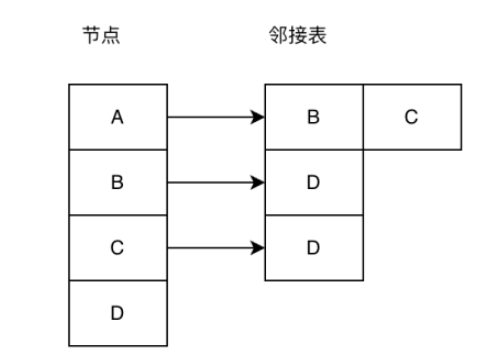
인접 목록: 인접 목록은 그래프 구조를 저장하는 효과적인 방법입니다. 아래 그림과 같이 왼쪽의 노드 배열은 그래프의 모든 노드를 저장하고 오른쪽의 인접 목록은 저장합니다. 노드의 인접한 노드.

소개

이번 글에서는 방향성 비순환 그래프의 알고리즘인 위상 정렬에 대해 이야기하겠습니다. 이는 주로 선행자와 후행자의 관계, 즉 현재를 완성할 때 사용됩니다. 작업, 먼저 완료해야 할 작업은 무엇입니까? 실제로 이것은 프로세스 제어에서 많이 사용됩니다. 아래 그림을 보면 A 항목을 먼저 완료해야 B 항목과 C 항목을 완료할 수 있습니다. B 항목과 C 항목은 평행하고 순서가 없지만 D 항목은 B 항목과 C 항목이 완료된 후에만 완료할 수 있습니다. 위상 정렬은 항목을 완성하기 위한 합리적인 순서를 찾는 데 도움이 될 수 있습니다. 동시에 위의 예를 살펴보겠습니다. 항목 A가 완료된 후 항목 B와 C가 먼저 완료되지 않습니다. 조건이 충족되므로 위상 정렬의 순서가 완전히 확실하지는 않습니다.

작업 과정

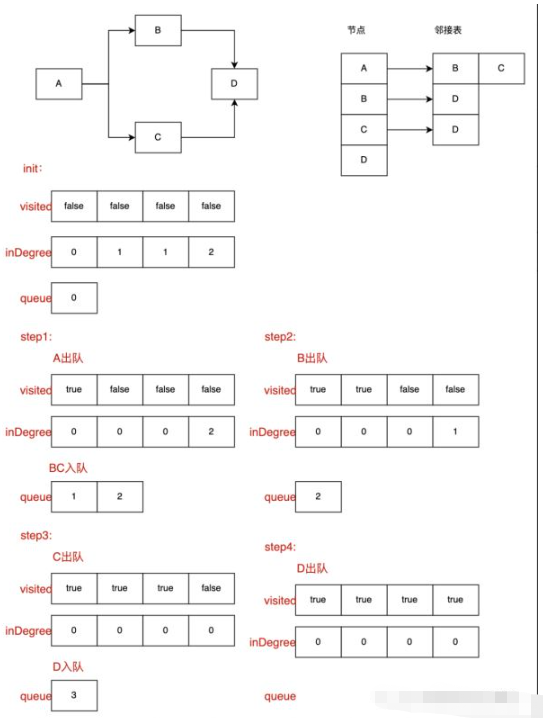
먼저, 위상 정렬에 해당하는 작업은 방향성 비순환 그래프입니다. 비순환 그래프의 경우 내차수가 0인 노드가 하나 이상 있어야 합니다. 현재 상황에서 동작을 위해서는 in-degree가 0인 노드를 찾아야 하는데, in-degree가 0이라는 것은 현재 노드에 선행 노드가 없거나, 선행 노드가 처리되어 직접 동작할 수 있다는 것을 의미합니다. 연산이 완료된 후에는 현재 노드의 후속 노드들의 in-degree를 모두 1씩 감소시키고, in-degree가 0인 노드를 다시 찾아 연산을 수행하게 되는데, 이는 재귀적 과정이다. 현재 상황에서 in-degree가 0인 노드는 모든 노드가 완료될 때까지 계속 처리됩니다.

데이터 구조

다음은 유향 그래프의 구조로, node는 현재 그래프의 모든 노드를 저장하고, adj는 첨자 노드에 해당하는 인접 점을 저장합니다. 그래프를 초기화할 때 노드 수를 지정하고 노드 배열과 인접 배열을 생성해야 합니다. 두 노드 사이에 간선을 설정하는 데, 즉 선행 노드의 인접 목록에 후속 노드를 추가하는 데 사용되는 addEdge라는 메서드를 제공합니다.

public static class Graph{
       /**
        * 节点个数
        */
       private Integer nodeSize;
       /**
        * 节点
        */
       private char[] node;
       /**
        * 邻接表
        */
       private LinkedList[] adj;

       public Graph(char[] node) {
           this.nodeSize = node.length;
           this.node = node;
           this.adj = new LinkedList[nodeSize];
           for (int i = 0 ; i < adj.length ; i++) {
               adj[i] = new LinkedList();
          }
      }
       /**
        * 在节点之间加边，前驱节点指向后继节点
        * @param front 前驱节点所在下标
        * @param end 后继节点所在下标
        */
       public void addEdge(int front, int end) {
           adj[front].add(end);
      }
  }

토폴로지 정렬

토폴로지 정렬은 먼저 두 개의 임시 배열, 대기열 및 inDegree 배열을 초기화하여 해당 첨자 노드의 차수를 저장합니다. 액세스된 각 노드에는 선행 노드가 완료되어야 하기 때문입니다. 즉, in-degree는 0입니다. 이 배열을 사용하면 이러한 노드를 비교적 빠르게 찾을 수 있습니다. 다른 하나는 방문 배열로, 여러 방문을 방지하기 위해 현재 노드를 방문했는지 여부를 표시합니다. 현재 상황에서는 0도입니다. (접근의 편의를 위해 우리는 모두 노드 첨자를 저장합니다. 1단계: inDegree 배열 및 방문 배열을 초기화합니다. 2단계: inDegree 배열을 탐색하고 indegree가 0인 모든 노드를 노드 큐에 넣습니다. 3단계: 노드를 종료합니다. Queue; 방문을 기반으로 현재 노드를 방문했는지 여부를 결정하고, 그렇다면 단계 3으로 돌아가고, 그렇지 않으면 현재 노드의 인접 노드의 차수를 -1로 설정합니다. , 인접한 노드의 in-degree가 0인지 확인하고, 0이면 직접 노드 큐에 넣고, 0이 아니면 3단계로 돌아갑니다.

/**
    * @param graph 有向无环图
    * @return 拓扑排序结果
    */
   public List<Character> toPoLogicalSort(Graph graph) {
       //用一个数组标志所有节点入度
       int[] inDegree = new int[graph.nodeSize];
       for (LinkedList list : graph.adj) {
           for (Object index : list) {
               ++ inDegree[(int)index];
          }
      }
       //用一个数组标志所有节点是否已经被访问
       boolean[] visited = new boolean[graph.nodeSize];
       //开始进行遍历
       Deque<Integer> nodes = new LinkedList<>();
       //将入度为0节点入队
       for (int i = 0 ; i < graph.nodeSize; i++) {
           if (inDegree[i] == 0) {
               nodes.offer(i);
          }
      }
       List<Character> result = new ArrayList<>();
       //将入度为0节点一次出队处理
       while (!nodes.isEmpty()) {
           int node = nodes.poll();
           if (visited[node]) {
               continue;
          }
           visited[node] = true;
           result.add(graph.node[node]);
           //将当前node的邻接节点入度-1；
           for (Object list : graph.adj[node]) {
               -- inDegree[(int)list];
               if (inDegree[(int)list] == 0) {
                   //前驱节点全部访问完毕，入度为0
                   nodes.offer((int) list);
              }
          }
      }
       return result;
  }

테스트 샘플 1

public static void main(String[] args) {
       ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
       //初始化一个图
       Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D'});
       graph.addEdge(0, 1);
       graph.addEdge(0,2);
       graph.addEdge(1,3);
       graph.addEdge(2,3);
       List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
  }

실행 결과

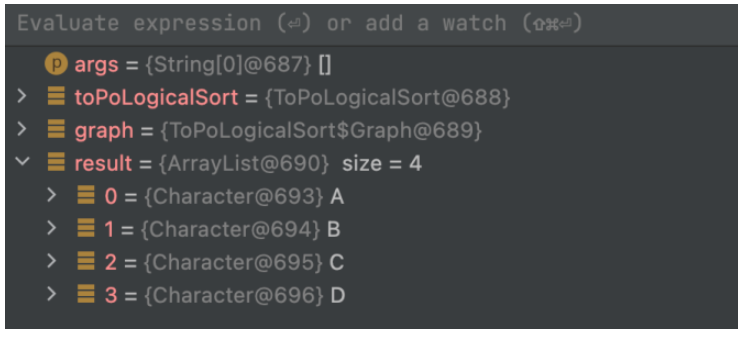
테스트 샘플 2

public static void main(String[] args) {
       ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
       //初始化一个图
       Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D','E','F','G','H'});
       graph.addEdge(0, 1);
       graph.addEdge(0,2);
       graph.addEdge(0,3);
       graph.addEdge(1,4);
       graph.addEdge(2,4);
       graph.addEdge(3,4);
       graph.addEdge(4,7);
       graph.addEdge(4,6);
       graph.addEdge(7,5);
       graph.addEdge(6,7);
       List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
  }

실행 결과

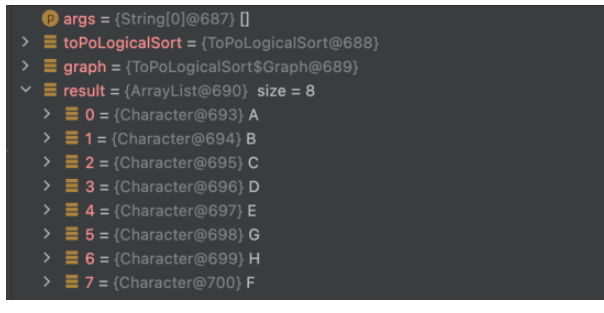
위 내용은 Java에서 토폴로지 정렬을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!