Python에서 의사결정 트리 분류 알고리즘을 구현하는 방법

사전 정보

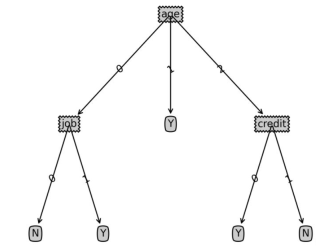
1. 결정 트리

재작성된 문장: 지도 학습에서 일반적으로 사용되는 분류 알고리즘은 결정 트리입니다. 이는 일련의 샘플을 기반으로 하며 각 샘플에는 일련의 속성과 해당 분류 결과가 포함됩니다. 이러한 샘플을 학습에 사용하면 알고리즘은 새로운 데이터를 올바르게 분류할 수 있는 의사결정 트리를 생성할 수 있습니다

2. 샘플 데이터

기존 사용자가 14명이고 이들의 개인 속성과 특정 제품 구매 여부에 대한 데이터가 다음과 같다고 가정합니다.

불안정 나쁨예 04>40Medium불안정나쁨예05>40 낮음안정 나쁨06>40낮음안정좋음아니요0730-40낮음안정 좋아요is08보통불안정나쁨아니요09낮음안정나쁨예 10>40 보통안정나쁨예11보통안정좋음예12 30-40중간불안정 좋음예1330-40높음안정나쁨예14>40보통 불안정좋아요아니요

특정 트리 분류 알고리즘

1. 데이터 세트 구성

처리를 용이하게 하기 위해 시뮬레이션 데이터는 다음 규칙에 따라 숫자 목록 데이터로 변환됩니다.

Age:

의 값이 할당됩니다. 소득: 낮음은 0, 중간은 1, 높음은 2

직장 특성: 불안정은 0, 안정적은 1

: 나쁨은 0, 좋음은 1

#创建数据集
def createdataset():
    dataSet=[[0,2,0,0,'N'],
            [0,2,0,1,'N'],
            [1,2,0,0,'Y'],
            [2,1,0,0,'Y'],
            [2,0,1,0,'Y'],
            [2,0,1,1,'N'],
            [1,0,1,1,'Y'],
            [0,1,0,0,'N'],
            [0,0,1,0,'Y'],
            [2,1,1,0,'Y'],
            [0,1,1,1,'Y'],
            [1,1,0,1,'Y'],
            [1,2,1,0,'Y'],
            [2,1,0,1,'N'],]
    labels=['age','income','job','credit']
    return dataSet,labels

통화 기능, 사용 가능한 데이터:

ds1,lab = createdataset()
print(ds1)
print(lab)

[[0, 2, 0, 0, ‘N’], [0, 2, 0, 1, ‘N’ ], [1, 2, 0, 0, ‘Y’], [2, 1, 0, 0, ‘Y’], [2, 0, 1, 0, ‘Y’], [2, 0, 1, 1, 'N'], [1, 0, 1, 1, 'Y'], [0, 1, 0, 0, 'N'], [0, 0, 1, 0 , ‘Y’], [2, 1, 1, 0, ‘Y’], [0, 1, 1, 1, ‘Y’], [1, 1, 0, 1, ‘Y’ ], [1, 2, 1, 0, ‘Y’], [2, 1, 0, 1, ‘N’]]
[‘나이’, ‘수입’, ‘직업’, &lsquo ;credit’]

2. 데이터 세트 정보 엔트로피

섀넌 엔트로피라고도 알려진 정보 엔트로피는 확률 변수에 대한 기대값입니다. 정보의 불확실성 정도를 측정합니다. 정보의 엔트로피가 클수록 정보를 파악하기가 더 어려워집니다. 정보를 처리하는 것은 정보를 명확하게 하는 것인데, 이는 엔트로피 감소 과정이다.

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        
        labelCounts[currentLabel] += 1            
        
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
    
    return shannonEnt

샘플 데이터 정보 엔트로피:

shan = calcShannonEnt(ds1)
print(shan)

0.9402859586706309

3. 정보 이득

정보 이득: 샘플 집합 X의 엔트로피를 줄이는 데 속성 A의 기여도를 측정하는 데 사용됩니다. 정보 획득이 클수록 X를 분류하는 데 더 적합합니다.

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0;bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntroy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prop = len(subDataSet)/float(len(dataSet))
            newEntroy += prop * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntroy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i    
    return bestFeature

위 코드는 정보 엔트로피 이득을 기반으로 ID3 결정 트리 학습 알고리즘을 구현합니다. 핵심 논리 원리는 다음과 같습니다. 속성 세트의 각 속성을 차례로 선택하고 이 속성의 값에 따라 샘플 세트를 여러 하위 세트로 나누고 이러한 하위 세트의 정보 엔트로피와 정보 엔트로피 간의 차이를 계산합니다. 샘플은 이 속성 분할의 정보 엔트로피 이득을 기반으로 하며, 모든 이득 중에서 가장 큰 이득에 해당하는 속성을 찾습니다. 이는 샘플 세트를 분할하는 데 사용되는 속성입니다.

샘플의 가장 좋은 분할 샘플 속성을 계산하면 결과가 0열에 표시됩니다. 이는 age 속성입니다.

col = chooseBestFeatureToSplit(ds1)
col

0

4 의사결정 트리 구성

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classList.iteritems(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
    return sortedClassCount[0][0]

#创建树的函数    
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        
    return myTree

majorityCnt code> 함수를 사용하여 처리합니다. 다음 상황은 최종 이상적인 의사결정 트리가 의사결정 분기를 따라 맨 아래에 도달해야 하며 모든 샘플의 분류 결과가 동일해야 합니다. 그러나 실제 샘플에서는 모든 속성이 일치하지만 분류 결과가 다른 것은 불가피합니다. 이 경우 <code>majorityCnt는 해당 샘플의 분류 라벨을 가장 많이 발생하는 분류 결과에 맞게 조정합니다. majorityCnt函数用于处理一下情况：最终的理想决策树应该沿着决策分支到达最底端时，所有的样本应该都是相同的分类结果。但是真实样本中难免会出现所有属性一致但分类结果不一样的情况，此时majorityCnt将这类样本的分类标签都调整为出现次数最多的那一个分类结果。

createTree

createTree는 핵심 작업 기능으로 모든 속성에 대해 ID3 정보 엔트로피 이득 알고리즘을 순차적으로 호출하여 계산하고 처리하며 최종적으로 의사결정 트리를 생성합니다.

5. 인스턴스화를 통해 결정 트리 구성

샘플 데이터를 사용하여 결정 트리 구성:

Tree = createTree(ds1, lab)
print("样本数据决策树：")
print(Tree)

샘플 데이터 결정 트리:
{‘age’: {0: {‘job’: {0: ‘ N’ , 1: ‘Y’}},
1: ‘Y’,

2: {’크레딧’: {0: ‘Y’, 1: ‘N’}}}

6. 테스트 샘플 분류

신규 사용자에게 특정 제품 구매 여부를 판단할 수 있는 정보 제공:

번호	나이	소득 범위	직업 특성	신용 등급	구매 결정
01		높음	불안정	나쁨 아니요

Age소득 범위업무 성격신용 등급lowstablegoodhighunstablegood

def classify(inputtree,featlabels,testvec):
    firststr = list(inputtree.keys())[0]
    seconddict = inputtree[firststr]
    featindex = featlabels.index(firststr)
    for key in seconddict.keys():
        if testvec[featindex]==key:
            if type(seconddict[key]).__name__=='dict':
                classlabel=classify(seconddict[key],featlabels,testvec)
            else:
                classlabel=seconddict[key]
    return classlabel

labels=['age','income','job','credit']
tsvec=[0,0,1,1]
print('result:',classify(Tree,labels,tsvec))
tsvec1=[0,2,0,1]
print('result1:',classify(Tree,labels,tsvec1))

결과: : N

포스트정보: 의사결정나무 code

다음 코드는 의사결정트리 그래픽, 비의사결정트리 알고리즘 포커스를 그리는 데 사용됩니다. 관심 있는 경우 학습에 참고할 수 있습니다

import matplotlib.pyplot as plt

decisionNode = dict(box, fc="0.8")
leafNode = dict(box, fc="0.8")
arrow_args = dict(arrow)

#获取叶节点的数目
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

#绘制连接线  
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

#绘制树结构  
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]     #the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

#创建决策树图形    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.savefig('决策树.png',dpi=300,bbox_inches='tight')
    plt.show()

위 내용은 Python에서 의사결정 트리 분류 알고리즘을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!