Python에서 @cache를 사용하는 방법

Python에서 @cache의 놀라운 용도는 무엇입니까?

캐싱 전략을 채택하면 공간을 시간으로 변환하여 컴퓨터 시스템 성능을 향상시킬 수 있습니다. 코드에서 캐싱의 역할은 코드의 실행 속도를 최적화하는 것입니다. 단, 메모리 사용량은 늘어납니다.

Python의 내장 모듈 functools에서는 데코레이터로 사용되는 캐싱을 구현하기 위해 고차 함수인 캐시()가 제공됩니다: @cache.

@cache 캐싱 기능 소개

캐시 소스 코드에서 캐시에 대한 설명은 다음과 같습니다. 단순 경량 무제한 캐시. 중국어로 번역하면 단순 경량 무제한 캐시입니다. 때로는 "메모이제이션"이라고도 합니다.

def cache(user_function, /):
    'Simple lightweight unbounded cache.  Sometimes called "memoize".'
    return lru_cache(maxsize=None)(user_function)

cache()에는 lru_cache() 함수를 호출하고 maxsize=None 매개변수를 전달하는 코드 한 줄만 있습니다. lru_cache()도 functools 모듈의 함수입니다. lru_cache()의 소스 코드를 확인하세요. maxsize의 기본값은 128이며, 이는 데이터가 128을 초과하면 삭제됩니다. LRU(Longest Unused) 알고리즘 데이터입니다. 캐시()가 maxsize를 None으로 설정하면 LRU 기능이 비활성화되고 캐시 수가 무한정 늘어날 수 있으므로 "무제한 캐시"라고 합니다.

lru_cache()는 오랫동안 사용되지 않은 LRU(Least Recent Used) 알고리즘을 사용하므로 함수 이름에 lru라는 글자가 3개 있습니다. 가장 적게 사용된 알고리즘의 메커니즘은 최근 기간에 데이터에 액세스하지 않았다고 가정하면 향후에도 해당 데이터에 액세스할 가능성도 매우 적다는 것입니다. LRU 알고리즘은 최근에 가장 적게 사용된 데이터를 제거하고 해당 데이터를 유지하도록 선택합니다. 데이터를 자주 사용합니다.

cache()는 Python 버전 3.9의 새로운 기능이고, lru_cache()는 Python 3.2 버전의 새로운 기능이며, 캐시()는 lru_cache() 기반의 캐시 수 제한을 해제하는데, 실제로 기술의 발전과 관련되어 있습니다. 하드웨어 성능이 크게 향상되었으므로 캐시()와 lru_cache()는 동일한 기능의 다른 버전일 뿐입니다.

lru_cache()는 본질적으로 함수에 대한 캐시 함수를 제공하는 데코레이터입니다. 들어오는 매개변수의 최대 크기 그룹을 캐시하고 다음에 동일한 매개변수로 함수가 호출될 때 높은 오버헤드나 높은 비용을 절약하기 위해 이전 결과를 직접 반환합니다. I/O. O 함수의 호출 시간입니다.

@cache의 애플리케이션 시나리오

Cache에는 정적 웹 콘텐츠 캐싱과 같은 광범위한 애플리케이션 시나리오가 있습니다. 사용자가 정적 웹 페이지에 액세스하는 기능에 @cache 데코레이터를 직접 추가할 수 있습니다.

일부 재귀 코드에서는 동일한 매개변수가 반복적으로 전달되어 함수 코드를 실행합니다. 캐시를 사용하면 반복 계산을 방지하고 코드의 시간 복잡도를 줄일 수 있습니다.

다음에는 @cache의 역할을 설명하기 위해 피보나치 수열을 예로 들어 보겠습니다. 이전 내용에 대해 아직 조금 이해가 되셨다면 예제를 읽어보시면 이해가 되실 거라 믿습니다.

피보나치 수열은 1, 1, 2, 3, 5, 8, 13, 21, 34,... 세 번째 숫자부터 시작하여 각 숫자는 처음 두 숫자의 합입니다. 대부분의 초보자는 피보나치 수열에 대한 코드를 작성했습니다. Python에서는 코드가 매우 간결합니다.

def feibo(n):
    # 第0个数和第1个数为1
    a, b = 1, 1
    for _ in range(n):
        # 将b赋值给a,将a+b赋值给b,循环n次
        a, b = b, a+b
    return a

물론 피보나치 수열 코드를 구현하는 방법은 여러 가지가 있습니다(적어도 5~6개). 이 기사에서는 @cache의 응용 시나리오를 설명하기 위해 재귀적 방법을 사용하여 코드를 작성합니다. 피보나치 수열. 다음과 같습니다:

def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    # 根据斐波那契数列的定义，其他情况递归返回前两个数之和
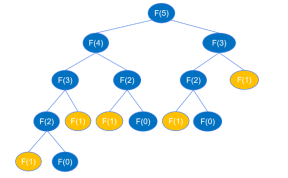
    return feibo_recur(n-1) + feibo_recur(n-2)

재귀 코드가 실행되면 아래 그림과 같이 feibo_recur(1) 및 feibo_recur(0)까지 계속 반복됩니다(6번째 숫자를 예로 사용).

F(5)를 찾으려면 F(4)와 F(3)을 먼저 찾아야 하고, F(4)를 찾으려면 F(3)과 F(2)를 먼저 찾아야 하고,.. 등, 재귀적으로 이 프로세스는 이진 트리의 깊이 우선 순회 프로세스와 유사합니다. 위의 재귀 호출 다이어그램에 따르면 높이 k인 이진 트리는 최대 2k-1개의 노드를 가질 수 있다고 알려져 있습니다. 이진 트리의 높이는 최대 2n-1개입니다. 재귀 함수 호출의 횟수는 최대 2n-1회이므로 재귀의 시간 복잡도는 O(2^n)입니다.

시간 복잡도가 O(2^n)일 때 n이 증가함에 따라 실행 시간이 매우 과장되게 변화합니다. 실제로 테스트해 보겠습니다.

import time
for i in [10, 20, 30, 40]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

출력:

10번째 피보나치 수: 89
n=10 비용 시간: 0.0
20번째 피보나치 수: 10946
n=20 비용 시간: 0.0015988349914550781
30번째 피보나치 수 보나치 번호: 1346269
n=30 Cost Time: 0.17051291465759277
40번째 피보나치 수: 165580141
n=40 Cost Time: 20.90010976791382

n이 매우 길면 매우 잘 실행되는 것을 실행 시간을 보면 알 수 있습니다. n이 증가할수록 실행 시간도 빨라집니다. 특히 n이 30과 40으로 점진적으로 증가하면 실행 시간이 특히 뚜렷하게 변합니다. 시간 변화 패턴을 보다 명확하게 확인하기 위해 추가 테스트를 수행했습니다.

for i in [41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

출력:

41번째 피보나치 수: 267914296
n=41 비용 시간: 33.77224683761597
42번째 피보나치 수: 433494437
n=42 비용 시간: 55.863986 6899414
43번째 피지 보나치 번호 : 701408733
n=43 비용 시간: 92.55108690261841

从上面的变化可以看到，时间是指数级增长的（大约按1.65的指数增长），这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度，假如要计算第50个斐波那契数列，差不多要等一个小时，非常不合理，也说明递归的实现方式运算量过大，存在明显的不足。如何解决这种不足，降低运算量呢？接下来看如何进行优化。

根据前面的分析，递归代码运算量大，是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2)，如示例图中，要得到 feibo_recur(5) ，feibo_recur(1) 调用了5次。随着 n 的增大，调用次数呈指数级增长，导致出现大量的重复操作，浪费了许多时间。

假如有一个地方将每个 n 的执行结果记录下来，当作“备忘录”，下次函数再接收到这个相同的参数时，直接从备忘录中获取结果，而不用去执行递归的过程，就可以避免这些重复调用。在 Python 中，可以创建一个字典或列表来当作“备忘录”使用。

temp = {}  # 创建一个空字典，用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    if n in temp:  # 如果temp字典中有n,则直接返回值,不调用递归代码
        return temp[n]
    else:
        # 如果字典中还没有第n个斐波那契数，则递归计算并保存到字典中
        temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
        return temp[n]

上面的代码中，创建了一个空字典用于存放每个 n 的执行结果。每次调用函数，都先查看字典中是否有记录，如果有记录就直接返回，没有记录就递归执行并将结果记录到字典中，再从字典中返回结果。这里的递归其实都只执行了一次计算，并没有真正的递归，如第一次传入 n 等于 5，执行 feibo_recur_temp(5)，会递归执行 n 等于 4, 3, 2, 1, 0 的情况，每个 n 计算过一次后 temp 中都有了记录，后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加，执行一次计算，所以时间复杂度是 O(n) 。

下面看一下代码的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)
print(temp)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}

可以观察到，代码的运行时间已经减少到小数点后很多位了（时间过短，只显示了0.0）。然而，temp 字典存储了每个数字的斐波那契数，这需要使用额外的内存空间，以换取更高的时间效率。

上面的代码也可以用列表来当“备忘录”，代码如下。

temp = [1, 1]
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    if n < len(temp):
        return temp[n]
    else:
        # 第一次执行时，将结果保存到列表中，后续直接从列表中取
        temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
        return temp[n]

现在，已经剖析了递归代码重复执行带来的时间复杂度问题，也给出了优化时间复杂度的方法，让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存，在下次以相同参数调用函数时直接返回上一次的结果，与上面的优化方式完全一致。

所以，只需要在递归函数上加 @cache 装饰器，递归的重复执行就可以解决，时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下：

from functools import cache
@cache
def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    return feibo_recur(n-1) + feibo_recur(n-2)

使用 @cache 装饰器，可以让代码更简洁优雅，并且让你专注于处理业务逻辑，而不需要自己实现缓存。下面看一下实际的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0

完美地解决了问题，所有运行时间都被精确到了小数点后数位（即使只显示 0.0），非常巧妙。若今后遇到类似情形，可以直接采用 @cache 实现缓存功能，通过“记忆化”处理。

补充：Python @cache装饰器

@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果，以便遇到相同参数可以直接给出答案。前者无限制存储数量，而后者通过设定maxsize限制存储数量的上限。

例：

@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
    print('开始计算a+b的值...')
    return a + b

可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果，都需要额外的空间。不过用装饰器可以省略额外空间代码，减少了出错的风险。

위 내용은 Python에서 @cache를 사용하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!