Java 데이터 구조의 힙을 만드는 방법

힙의 속성

힙은 논리적으로 완전한 이진 트리이고 힙은 물리적으로 배열에 저장됩니다.

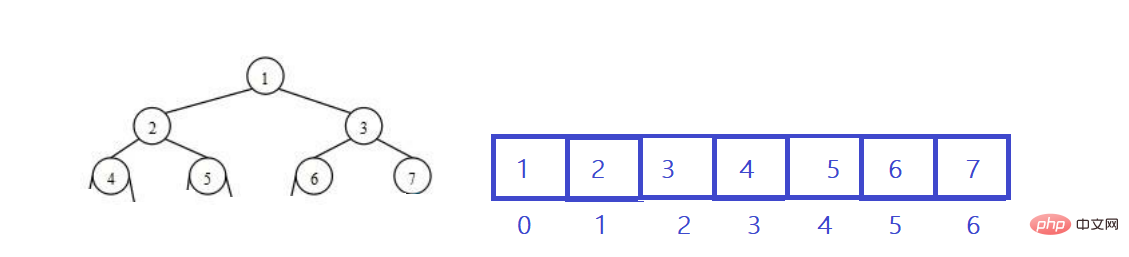
요약: 완전한 이진 트리는 레벨 순서 탐색을 사용하여 배열에 저장됩니다. 이 방법의 주요 용도는 힙 표현입니다.

그리고 부모의 첨자를 알면

다음: 왼쪽 자식(왼쪽) 첨자 = 2 * 부모 + 1;

오른쪽 자식(오른쪽) 첨자 = 2 * 부모 + 2;

자식의 첨자(왼쪽과 오른쪽 구분 없음)는 다음과 같습니다.

Parent(부모) 첨자 = (자식 - 1) / 2;

힙의 분류

큰 힙: 루트 노드가 왼쪽 노드보다 크고 오른쪽 자식 노드 완전한 이진 트리(부모 노드가 자식 노드보다 큼)를 빅 힙, 빅 루트 힙 또는 최대 힙이라고 합니다.

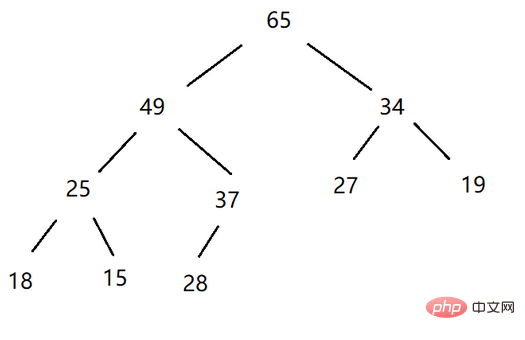
작은 힙: 루트 노드가 두 개의 왼쪽 및 오른쪽 자식 노드보다 작은 완전한 이진 트리를 작은 힙(상위 노드가 자식 노드보다 작음) 또는 작은 루트 힙이라고 합니다. 최소 힙.

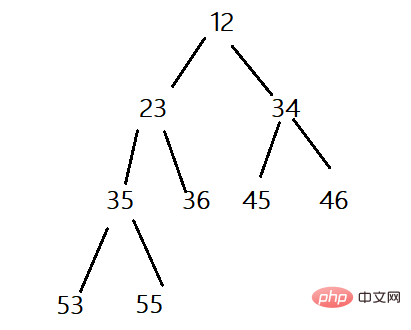
힙의 하향 조정

이제 논리적으로 완전한 이진 트리인 배열이 있습니다. 루트 노드부터 시작하는 하향 조정 알고리즘을 통해 이를 작은 힙이나 큰 힙으로 조정할 수 있습니다. 하향 조정 알고리즘에는 전제가 있습니다. 왼쪽 및 오른쪽 하위 트리는 조정되기 전에 힙이어야 합니다.

작은 힙을 예로 들어보겠습니다.

1. 먼저 왼쪽과 오른쪽 하위 노드를 비교하여 최소값을 취합니다.

2. 더 작은 하위 노드를 상위 노드와 비교합니다. 하위 노드

3. 하위 노드의 첨자가 범위를 벗어나면 사이클이 계속된다는 뜻입니다.

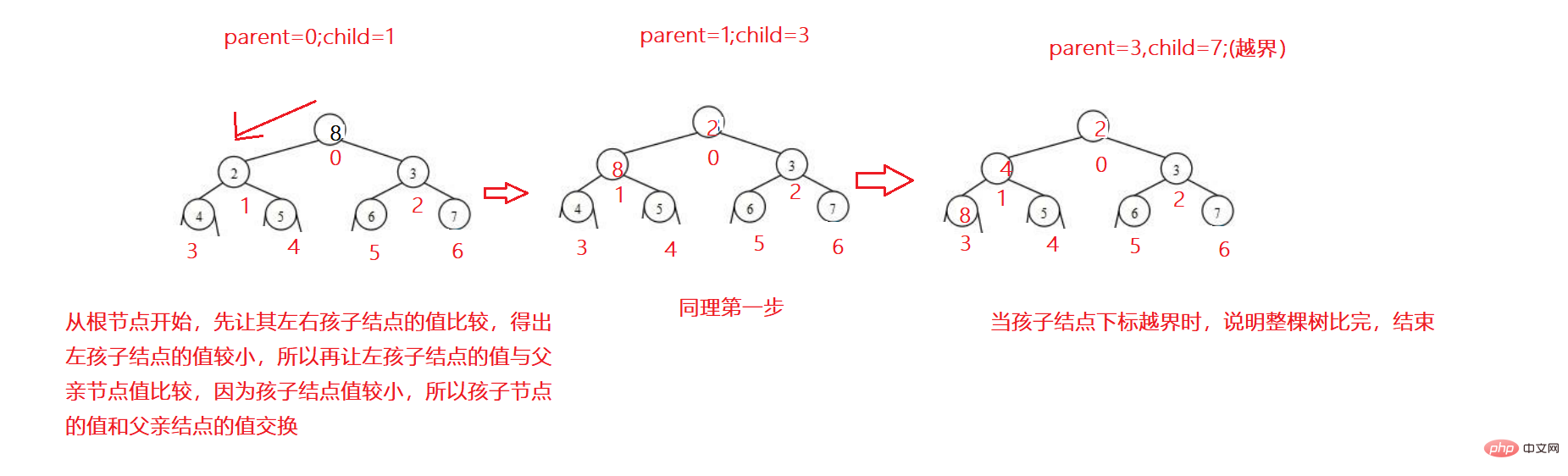
코드 예:

 //parent: 每棵树的根节点
 //len: 每棵树的调整的结束位置
public void shiftDown(int parent,int len){
        int child=parent*2+1; //因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以最起码是有左孩子的，至少有1个孩子
        while(child<len){
            if(child+1<len && elem[child]<elem[child+1]){
                child++;//两孩子结点比较取较小值
            }
            if(elem[child]<elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                parent=child;
                child=parent*2+1;
            }else{
                break;
            }
        }
    }

힙 구축

배열이 주어지면 이 배열은 논리적으로 완전한 이진 트리로 간주될 수 있지만 아직 힙은 아닙니다(왼쪽 및 오른쪽 하위 트리가 둘 다 크거나 크지 않음). 작은) 힙), 이제 알고리즘을 사용하여 힙(큰 또는 작은 힙)으로 만듭니다. 어떻게 해야 하나요? 여기에서는 리프가 아닌 마지막 노드의 첫 번째 하위 트리부터 조정을 시작하고 이를 루트 노드의 트리까지 조정한 다음 더미로 조정할 수 있습니다. 여기서는 방금 작성한 하향 조정을 사용하겠습니다.

public void creatHeap(int[] arr){
        for(int i=0;i<arr.length;i++){
            elem[i]=arr[i];
            useSize++;
        }
        for(int parent=(useSize-1-1)/2;parent>=0;parent--){//数组下标从0开始
            shiftDown(parent,useSize);
        }
    }

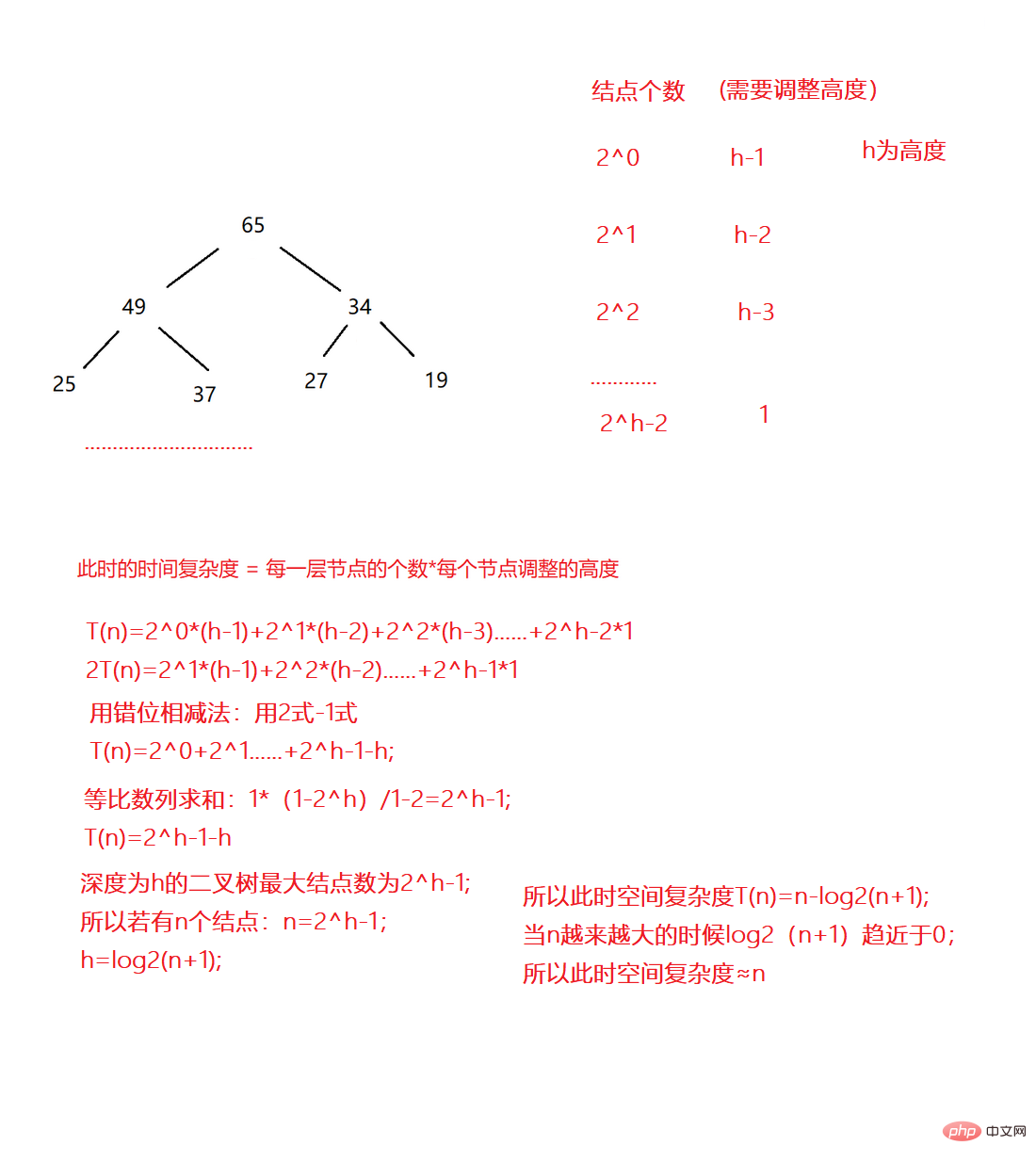
힙 구축의 공간 복잡도는 O(N)입니다. 힙은 완전 이진 트리이고 완전 이진 트리도 완전 이진 트리이기 때문입니다(최악의 경우). 증명해 보세요.

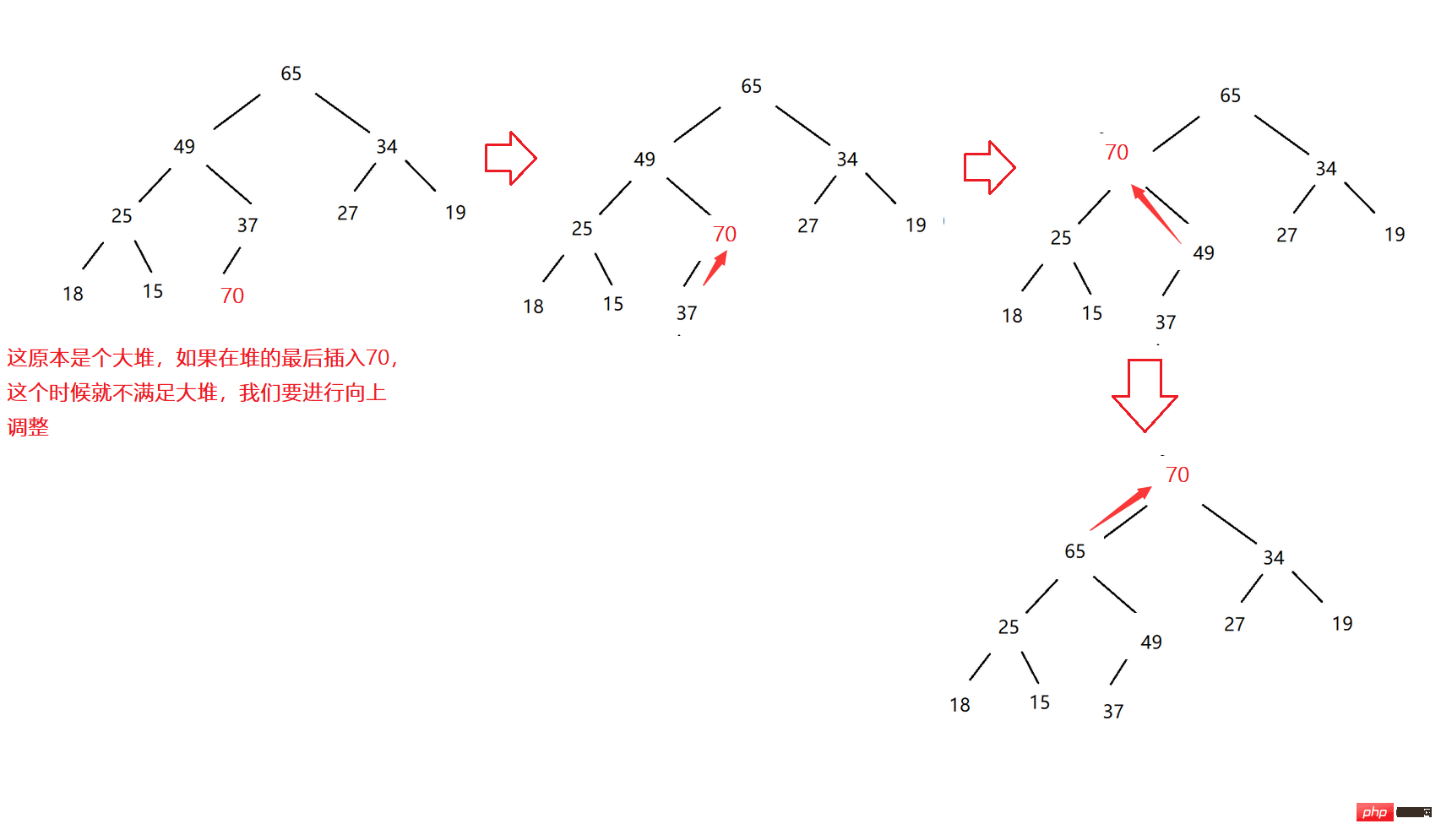
힙을 위쪽으로 조정해야 합니다

이제 힙이 있으므로 힙 끝에 데이터를 삽입한 다음 힙의 구조를 계속 유지하도록 조정해야 합니다. 이것이 위쪽 조정입니다. .

큰 힙을 예로 들어보세요:

코드 예:

public void shiftup(int child){
        int parent=(child-1)/2;
        while(child>0){
            if(elem[child]>elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

힙의 일반적인 작업

Enqueue

힙에 요소를 추가하려면, 즉 요소를 마지막 위치에 추가하고 그런 다음 위쪽으로 조정하십시오.

public boolean isFull(){
        return elem.length==useSize;
    }
public void offer(int val){
        if(isFull()){
            elem= Arrays.copyOf(elem,2*elem.length);//扩容
        }
        elem[useSize++]=val;
        shiftup(useSize-1);
    }

Dequeue

힙의 요소를 삭제하려면 힙의 최상위 요소를 마지막 요소로 바꾼 다음 전체 배열의 크기를 1만큼 줄이고 마지막으로 아래쪽으로 조정하여 스택의 최상위 요소를 삭제합니다. .

public boolean isEmpty(){
        return useSize==0;
    }
public int poll(){
        if(isEmpty()){
            throw new RuntimeException("优先级队列为空");
        }
        int tmp=elem[0];
        elem[0]=elem[useSize-1];
        elem[useSize-1]=tmp;
        useSize--;
        shiftDown(0,useSize);
        return tmp;
    }

팀 리더 요소 가져오기

public int peek() {
        if (isEmpty()) {
            throw new RuntimeException("优先级队列为空");
        }
        return elem[0];
    }

TopK 질문

6개의 데이터가 주어졌을 때 가장 큰 데이터 상위 3개를 찾으세요. 이때 힙을 어떻게 사용합니까?

문제 해결 아이디어:

1. 상위 K개의 가장 큰 요소를 찾으려면 작은 루트 힙을 구축해야 합니다.

2. 처음으로 K개의 가장 작은 요소를 찾으려면 큰 루트 힙을 구축해야 합니다.

3. K번째로 큰 요소입니다. 작은 힙을 만들고, 힙의 맨 위 요소가 K번째로 큰 요소입니다.

4. K번째로 작은 요소입니다. 큰 힙을 구축하고 힙의 최상위 요소가 K번째로 큰 요소입니다.

Example

예: 처음 n개의 가장 큰 데이터 찾기

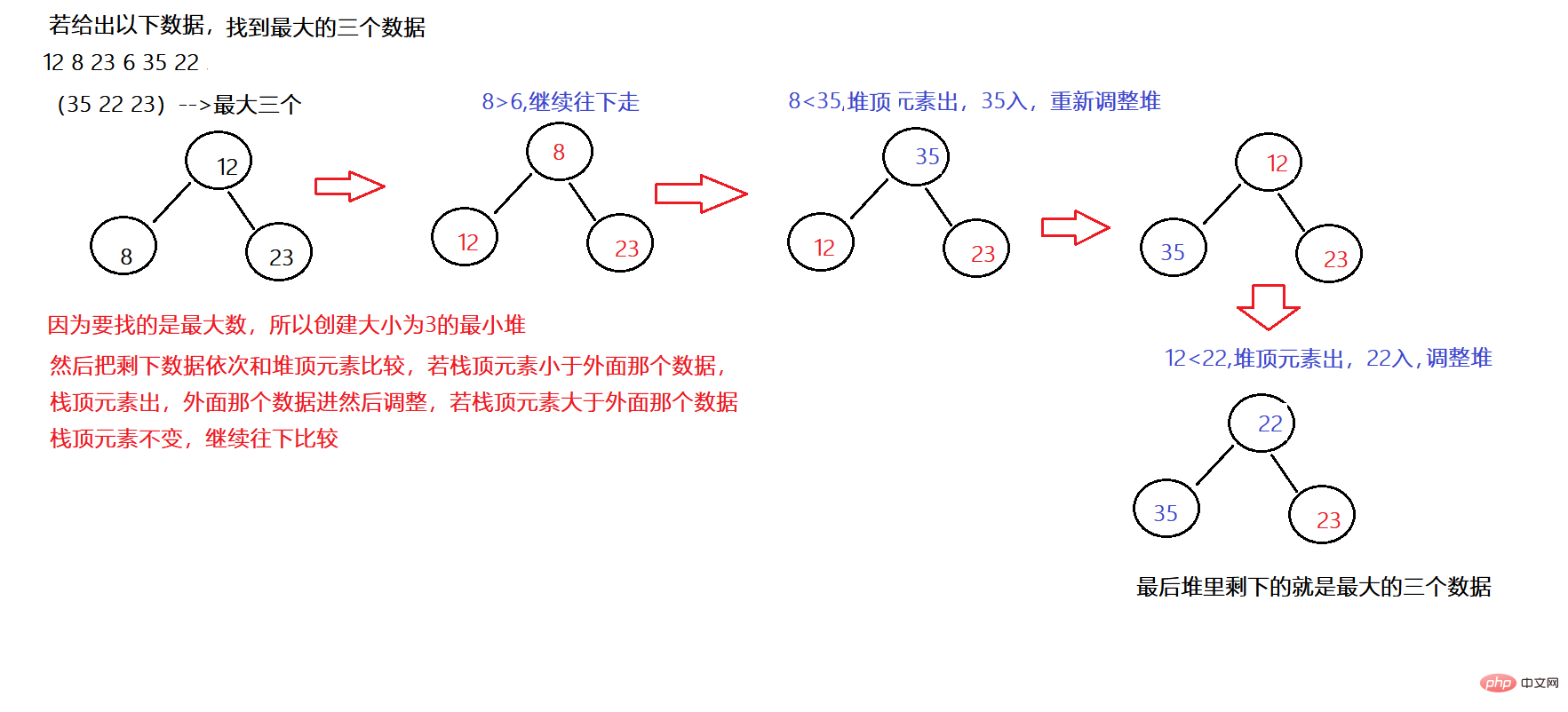
코드 예:

 public static int[] topK(int[] array,int k){
        //创建一个大小为K的小根堆
        PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1-o2;
            }
        });
        //遍历数组中元素，将前k个元素放入队列中
        for(int i=0;i<array.length;i++){
            if(minHeap.size()<k){
                minHeap.offer(array[i]);
            }else{
                //从k+1个元素开始，分别和堆顶元素比较
                int top=minHeap.peek();
                if(array[i]>top){
                    //先弹出后存入
                    minHeap.poll();
                    minHeap.offer(array[i]);
                }
            }
        }
        //将堆中元素放入数组中
        int[] tmp=new int[k];
        for(int i=0;i< tmp.length;i++){
            int top=minHeap.poll();
            tmp[i]=top;
        }
        return tmp;
    }
    public static void main(String[] args) {
        int[] array={12,8,23,6,35,22};
        int[] tmp=topK(array,3);
        System.out.println(Arrays.toString(tmp));
    }

Result:

Array sort

또한 배열을 작은 것에서 큰 것으로 정렬하려면, 큰 루트 파일을 사용해야 할까요, 아니면 작은 루트 파일을 사용해야 할까요?

---->Dagendui

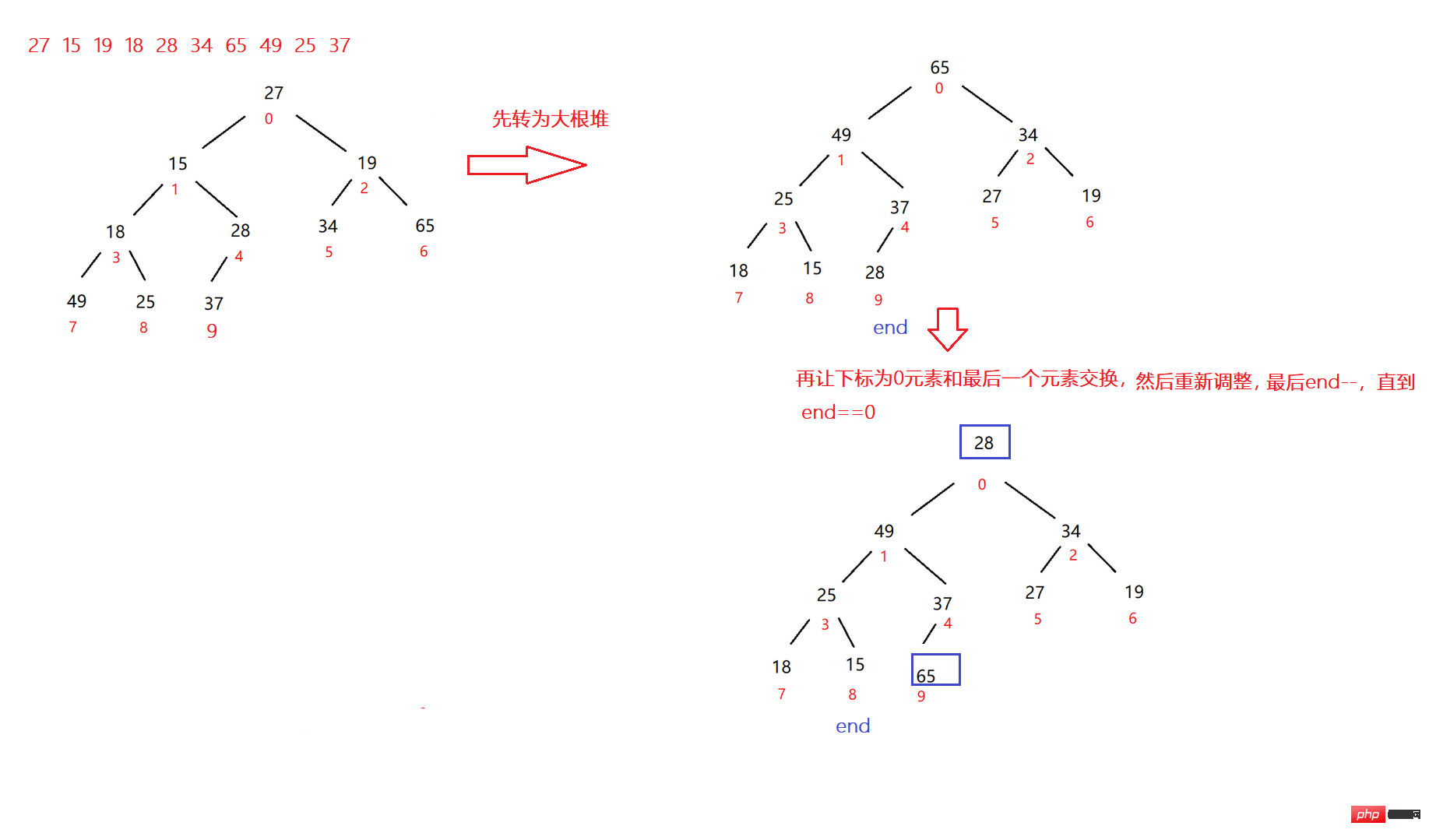
코드 예:

  public void heapSort(){
        int end=useSize-1;
        while(end>0){
            int tmp=elem[0];
            elem[0]=elem[end];
            elem[end]=tmp;
            shiftDown(0,end);//假设这里向下调整为大根堆
            end--;
        }
    }

위 내용은 Java 데이터 구조의 힙을 만드는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!