Java에서 상위 10개 정렬 알고리즘을 구현하는 방법
- 王林앞으로
- 2023-05-15 15:55:061440검색
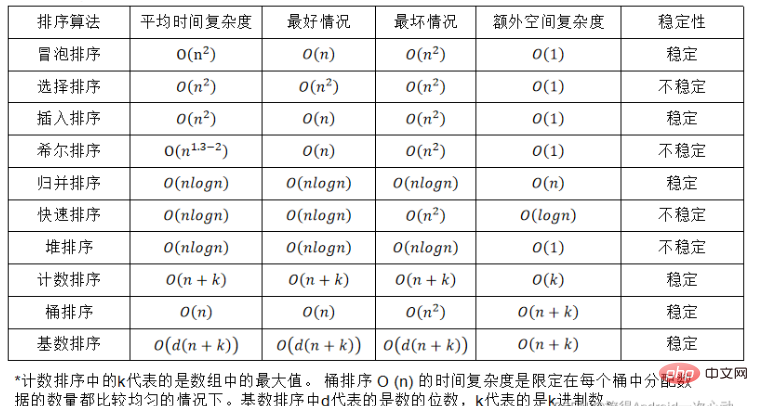
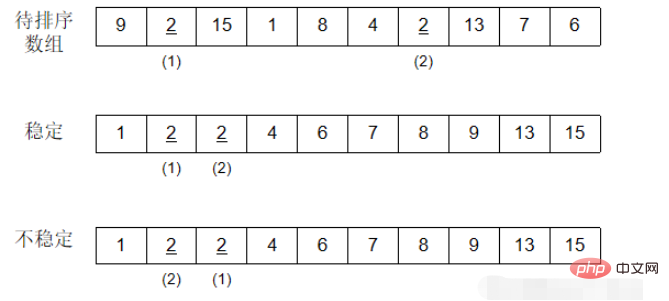
정렬 알고리즘의 안정성:
정렬할 레코드 순서에 동일한 키워드를 가진 여러 레코드가 있다고 가정합니다. 정렬 후에도 이러한 레코드의 상대적 순서는 변경되지 않고 유지됩니다. 원래 시퀀스에서 a[i]=a[j]이고 a[i]가 a[j] 앞에 있고 a[i]가 정렬 후에도 여전히 a[j] 앞에 있으면 이 정렬 알고리즘은 다음과 같습니다. 안정적이라고 하고, 그렇지 않으면 불안정하다고 합니다.
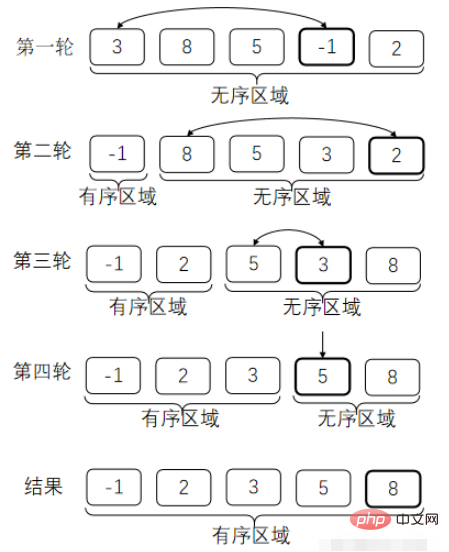
1. 선택 정렬
매번 정렬할 요소 중 가장 작은 요소를 선택하여 1, 2, 3... 위치의 요소와 차례로 교환합니다. 이는 어레이 전면에 정렬된 영역을 형성합니다. 스왑이 수행될 때마다 정렬된 영역의 길이가 1씩 증가합니다.
public static void selectionSort(int[] arr){
//细节一：这里可以是arr.length也可以是arr.length-1
for (int i = 0; i < arr.length-1 ; i++) {
int mini = i;
for (int j = i+1; j < arr.length; j++) {
//切换条件，决定升序还是降序
if(arr[mini]>arr[j]) mini =j;
}
swap(arr,mini,i);
}
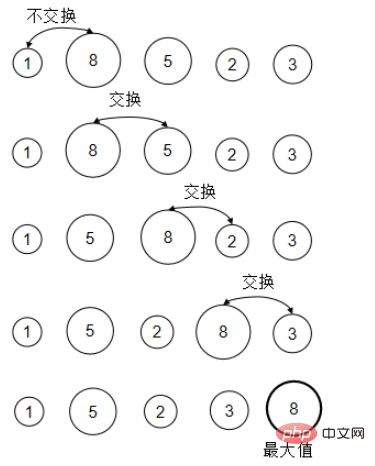
}2. 버블 정렬
순서가 잘못된 경우 이 방법으로 각 비교 후에 가장 큰 숫자가 있어야 할 위치에 배치됩니다. 위치. (가장 큰 버블을 상위 레이어로 가져가는 것과 같습니다.)
잘못된 순서의 의미는 다음과 같습니다. 오름차순으로 정렬합니다. 이후 값은 이전 값보다 크거나 같아야 합니다.
public static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
//记录本次有没有进行交换的操作
boolean flag = false;
//保存在头就动头，保存在尾就动尾
for(int j =0 ; j < arr.length-1-i ; j++){
//升序降序选择地
if(arr[j] > arr[j+1])
{
swap(arr,j,j+1);
flag = true;
}
}
//如果本次没有进行交换操作，表示数据已经有序
if(!flag){break;} //程序结束
}
}3. 삽입 정렬
삽입 정렬은 실제로 포커를 할 때 카드를 뽑는 과정으로 이해될 수 있습니다. , 카드를 있어야 할 곳에 삽입하십시오. 모든 카드를 터치한 후에는 모든 카드가 순서대로 정렬됩니다.
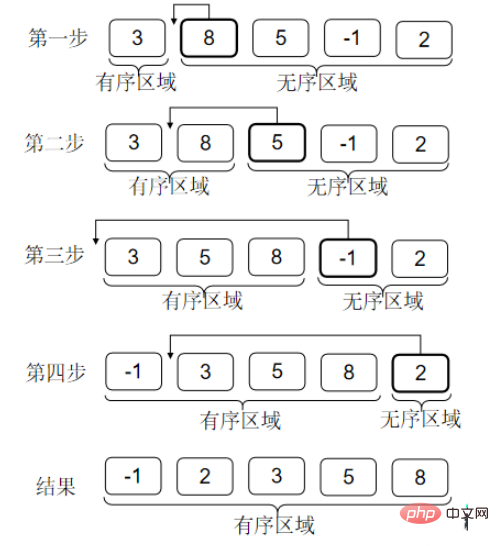
생각하기: 배열 앞에 정렬된 영역이 형성됩니다. 그런 다음 현재 숫자가 삽입되어야 하는 위치를 찾으면 이진 분할을 사용하여 삽입 정렬의 복잡성을 O(nlogn)로 최적화할 수 있습니까? ?
위치는 로그 복잡도로 찾을 수 있습니다. 중요한 점은 배열을 사용하여 데이터를 저장하는 경우 삽입 중에 데이터를 다시 이동하는 복잡성이 여전히 O(n)이라는 것입니다. 연결리스트를 사용하면 위치를 찾아 삽입하는 것은 O(1)이지만, 연결리스트를 둘로 나눌 수는 없다.
public static void insertSort(int[] arr){
//从第二个数开始，把每个数依次插入到指定的位置
for(int i = 1 ; i < arr.length ; i++)
{
int key = arr[i];
int j = i-1;
//大的后移操作
while(j >= 0 && arr[j] > key)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}4. Hill 정렬
Hill 정렬은 1959년 Donald Shell이 제안한 정렬 알고리즘입니다. 직접 삽입 정렬을 개선하고 효율적인 버전입니다. Hill 정렬을 위해서는 일련의 데이터를 증분 순서로 준비해야 합니다.
이 데이터 집합은 다음 세 가지 조건을 충족해야 합니다.
1. 데이터가 내림차순으로 정렬됩니다.
2. 데이터의 최대값이 정렬할 배열의 길이보다 작습니다.
3. 데이터의 최소값은 1입니다. + 위의 요구 사항을 충족하는 배열은 증분 시퀀스로 사용할 수 있지만 증분 시퀀스가 다르면 정렬 효율성에 영향을 미칩니다. 여기서는 {5,3,1}을 증분 시퀀스로 사용하여 설명합니다
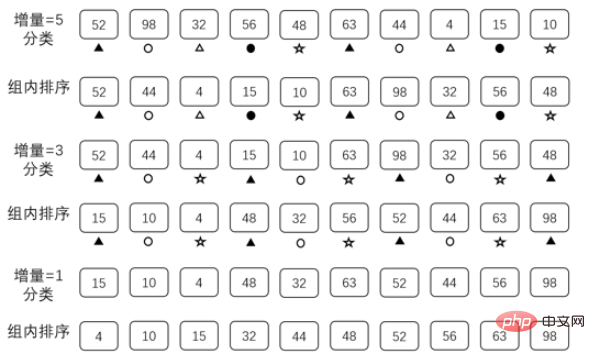최적화 이유: O(n)과 O(n^2)의 차이가 크지 않도록 데이터 양을 줄입니다.
public static void shellSort(int[] arr){
//分块处理
int gap = arr.length/2; //增量
while(1<=gap)
{
//插入排序：只不过是与增量位交换
for(int i = gap ; i < arr.length ; i++)
{
int key = arr[i];
int j = i-gap;
while(j >= 0 && arr[j] > key)
{
arr[j+gap] = arr[j];
j-=gap;
}
arr[j+gap] = key;
}
gap = gap/2;
}
} 5. 힙 정렬
은 큰 루트 힙과 작은 루트 힙의 두 가지 유형으로 나누어진 완전한 이진 트리입니다.
O(1)에서 최대/최소 값을 취하고, O(1)에서 최대/최소 값을 삭제할 수 있습니다. O(logn), O(logn)에서 최대/최소값 삭제 요소 삽입
MIN-HEAPIFY(i) 작업:
완전 이진 트리에서 특정 노드 i의 왼쪽 하위 트리와 오른쪽 하위 트리가 있다고 가정합니다. i 노드의 왼쪽 자식이 left_i라고 가정하면 둘 다 작은 루트 힙의 속성을 충족합니다. i 노드의 오른쪽 자식은 rigℎt_i입니다. a[i]가 a[left_i] 또는 a[rigℎt_i]보다 크면 i 노드가 루트 노드인 전체 하위 트리는 작은 루트 힙의 속성을 충족하지 않습니다. 이제 i를 넣어야 합니다. 루트 노드로서 루트 노드의 하위 트리는 작은 루트 힙으로 조정됩니다.
//堆排序
public static void heapSort(int[] arr){
//开始调整的位置为最后一个叶子节点
int start = (arr.length - 1)/2;
//从最后一个叶子节点开始遍历，调整二叉树
for (int i = start; i >= 0 ; i--){
maxHeap(arr, arr.length, i);
}
for (int i = arr.length - 1; i > 0; i--){
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
maxHeap(arr, i, 0);
}
}
//将二叉树调整为大顶堆
public static void maxHeap(int[] arr, int size, int index){
//建立左子节点
int leftNode = 2 * index + 1;
//建立右子节点
int rightNode = 2 * index + 2;
int maxNode = index;
//左子节点的值大于根节点时调整
if (leftNode < size && arr[leftNode] > arr[maxNode]){
maxNode = leftNode;
}
//右子节点的值大于根节点时调整
if (rightNode < size && arr[rightNode] > arr[maxNode]){
maxNode = rightNode;
}
if (maxNode != index){
int temp = arr[maxNode];
arr[maxNode] = arr[index];
arr[index] = temp;
//交换之后可能会破坏原来的结构，需要再次调整
//递归调用进行调整
maxHeap(arr, size, maxNode);
}
}
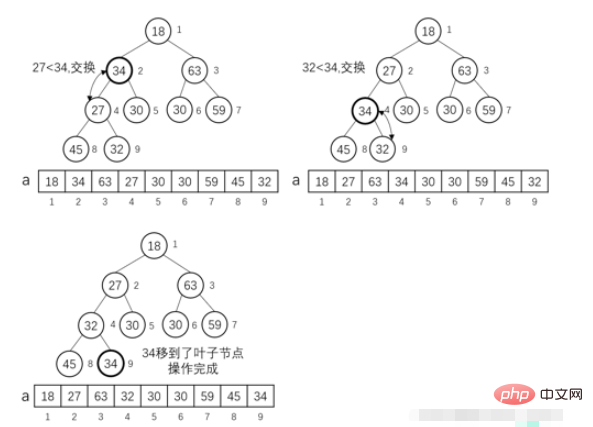저는 큰 뿌리 더미를 사용합니다. 정렬 과정은 다음과 같이 요약할 수 있습니다. 먼저 왼쪽 뿌리, 그 다음 오른쪽 뿌리(어떻게 쓰는지 보세요) ->각 뿌리는 위로 갔다가 아래로 내려갑니다. (왼쪽, 오른쪽, 위쪽 및 아래쪽)
6. 병합 정렬
병합 정렬은 분할 정복 방법의 대표적인 응용 방법입니다. 먼저 분할 정복 방법을 소개하겠습니다. 분할 정복 방법은 복잡한 문제를 분할하는 것입니다. 두 개 이상의 동일하거나 유사한 하위 문제로 나눈 다음 하위 문제를 더 작은 하위 문제로 나누고... 최종 하위 문제가 직접 해결될 수 있을 만큼 작아질 때까지 솔루션을 하위 문제에 결합합니다. -원래 문제에 대한 해결책을 찾는 문제.
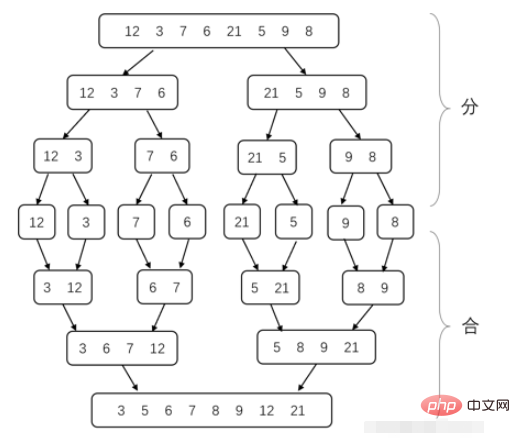
병합 정렬 분해 하위 문제의 프로세스는 배열의 길이가 1이 될 때까지 배열을 매번 2개의 부분으로 나누는 것입니다(하나의 숫자만 있는 배열이 주문되기 때문입니다). 그런 다음 인접한 정렬된 배열을 하나의 정렬된 배열로 병합합니다. 모두 합쳐질 때까지 전체 배열이 정렬됩니다. 이제 해결해야 할 문제는 두 개의 정렬된 배열을 하나의 정렬된 배열로 병합하는 방법입니다. 사실, 매번 두 배열의 가장 작은 두 개의 현재 요소를 비교하는 것입니다. 어느 쪽이든 더 작은 것을 선택하세요
array a |
array b |
설명 |
대답 array |
| 2,5,7 |
1,3,4 |
1 |
1 |
2,5,7 | 1,3,4 |
2 |
1,2 |
2,5 ,7 |
1,3, 4 |
3 |
1,2,3 |
|
2,5,7 |
1,3,4 |
4 |
1,2,3,4 |
2,5,7 | 1,3,4 |
배열 b에 요소가 없습니다. 5 |
1,2,3,4,5 |
2,5,7 |
1을 취하세요. ,3,4 |
배열 b에 요소가 없습니다. 예, 7 |
1,2,3,4,5,7 |
public static void mergeSort(int[] arr, int low, int high){
int middle = (high + low)/2;
if (low < high){
//递归排序左边
mergeSort(arr, low, middle);
//递归排序右边
mergeSort(arr, middle +1, high);
//将递归排序好的左右两边合并
merge(arr, low, middle, high);
}
}
public static void merge(int[] arr, int low, int middle, int high){
//存储归并后的临时数组
int[] temp = new int[high - low + 1];
int i = low;
int j = middle + 1;
//记录临时数组中存放数字的下标
int index = 0;
while (i <= middle && j <= high){
if (arr[i] < arr[j]){
temp[index] = arr[i];
i++;
} else {
temp[index] = arr[j];
j++;
}
index++;
}
//处理剩下的数据
while (j <= high){
temp[index] = arr[j];
j++;
index++;
}
while (i <= middle){
temp[index] = arr[i];
i++;
index++;
}
//将临时数组中的数据放回原来的数组
for (int k = 0; k < temp.length; ++k){
arr[k + low] = temp[k];
}
}七.快速排序
快速排序的工作原理是：从待排序数组中随便挑选一个数字作为基准数，把所有比它小的数字放在它的左边，所有比它大的数字放在它的右边。然后再对它左边的数组和右边的数组递归进行这样的操作。
全部操作完以后整个数组就是有序的了。 把所有比基准数小的数字放在它的左边，所有比基准数大的数字放在它的右边。这个操作，我们称为“划分”(Partition)。
//快速排序
public static void QuickSort1(int[] arr, int start, int end){
int low = start, high = end;
int temp;
if(start < end){
int guard = arr[start];
while(low != high){
while(high > low && arr[high] >= guard) high--;
while(low < high && arr[low] <= guard) low++;
if(low < high){
temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
}
arr[start] = arr[low];
arr[low] = guard;
QuickSort1(arr, start, low-1);
QuickSort1(arr, low+1, end);
}
}
//快速排序改进版(填坑法)
public static void QuickSort2(int[] arr, int start, int end){
int low = start, high = end;
if(start < end){
while(low != high){
int guard = arr[start];//哨兵元素
while(high > low && arr[high] >= guard) high--;
arr[low] = arr[high];
while(low < high && arr[low] <= guard) low++;
arr[high] = arr[low];
}
arr[low] = guard;
QuickSort2(arr, start, low-1);
QuickSort2(arr, low+1, end);
}
}八.鸽巢排序
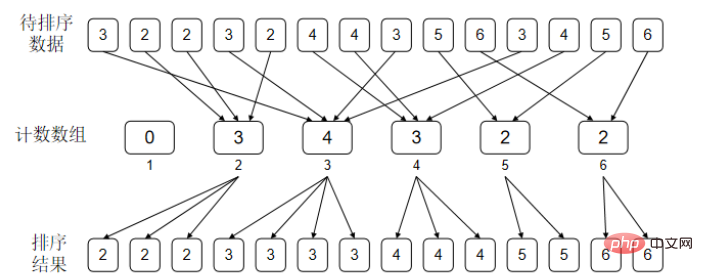
计算一下每一个数出现了多少次。举一个例子，比如待排序的数据中1出现了2次，2出现了0次，3出现了3次，4出现了1次，那么排好序的结果就是{1.1.3.3.3.4}。
//鸽巢排序
public static void PigeonholeSort(int[] arr){
//获取最大值
int k = 0;
for (int i = 0; i < arr.length; i++) {
k = Math.max(k,arr[i]);
}
//创建计数数组并且初始化为0
int[] cnt = new int[k+10];
for(int i = 0 ; i <= k ; i++) { cnt[i]=0; }
for(int i = 0 ; i < arr.length ;i++) { cnt[arr[i]]++; }
int j = 0;
for(int i = 0 ; i <=k ; i++)
{
while(cnt[i]!=0)
{
arr[j]=i;
j++;
cnt[i]--;
}
}
}鸽巢排序其实算不上是真正意义上的排序算法，它的局限性很大。只能对纯整数数组进行排序，举个例子，如果我们需要按学生的成绩进行排序。是一个学生+分数的结构那就不能排序了。
九.计数排序
先考虑这样一个事情：如果对于待排序数据中的任意一个元素 a[i]，我们知道有 m 个元素比它小，那么我们是不是就可以知道排好序以后这个元素应该在哪个位置了呢？（这里先假设数据中没有相等的元素）。计数排序主要就是依赖这个原理来实现的。
比如待排序数据是{2,4,0,2,4} 先和鸽巢一样做一个cnt数组{1,0,2,0,2} 0,1,2,3,4
此时cnt[i]表示数据i出现了多少次，
然后对cnt数组做一个前缀和{1,1,3,3,5} ：0,1,2,3,4
此时cnt[i]表示数据中小于等于i的数字有多少个
待排序数组 |
计数数组 |
说明 |
答案数组ans |
2,4,0,2,4 |
1,1,3,3,5 |
初始状态 |
null,null,null,null,null, |
2,4,0,2,4 |
1,1,3,3,5 |
cnt[4]=5，ans第5位赋值，cnt[4]-=1 |
null,null,null,null,4 |
2,4,0,2,4 |
1,1,3,3,4 |
cnt[2]=3，ans第3位赋值，cnt[2]-=1 |
null,null,2 null,4 |
2,4,0,2,4 |
1,1,2,3,4 |
cnt[0]=1，ans第1位赋值，cnt[0]-=1 |
0,null,2,null,4 |
2,4,0,2,4 |
0,1,2,3,4 |
cnt[4]=4，ans第4位赋值，cnt[4]-=1 |
0,null,2,4,4 |
2,4,0,2,4 |
0,1,2,3,3 |
cnt[2]=2，ans第2位赋值，cnt[2]-=1 |
0,2,2,4,4 |
十.基数排序
基数排序是通过不停的收集和分配来对数据进行排序的。
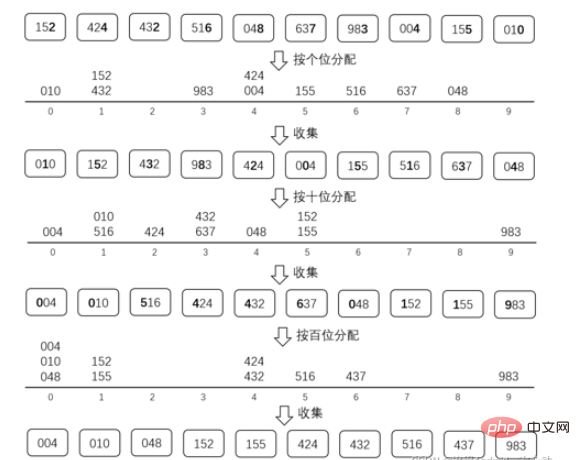
因为是10进制数，所以我们准备十个桶来存分配的数。
最大的数据是3位数，所以我们只需要进行3次收集和分配。
需要先从低位开始收集和分配（不可从高位开始排，如果从高位开始排的话，高位排好的顺序会在排低位的时候被打乱，有兴趣的话自己手写模拟一下试试就可以了）
在收集和分配的过程中，不要打乱已经排好的相对位置
比如按十位分配的时候，152和155这两个数的10位都是5，并且分配之前152在155的前面，那么收集的时候152还是要放在155之前的。
//基数排序
public static void radixSort(int[] array) {
//基数排序
//首先确定排序的趟数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
int time = 0;
//判断位数;
while (max > 0) {
max /= 10;
time++;
}
//建立10个队列;
List<ArrayList> queue = new ArrayList<ArrayList>();
for (int i = 0; i < 10; i++) {
ArrayList<Integer> queue1 = new ArrayList<Integer>();
queue.add(queue1);
}
//进行time次分配和收集;
for (int i = 0; i < time; i++) {
//分配数组元素;
for (int j = 0; j < array.length; j++) {
//得到数字的第time+1位数;
int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
ArrayList<Integer> queue2 = queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count = 0;//元素计数器;
//收集队列元素;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList<Integer> queue3 = queue.get(k);
array[count] = queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}위 내용은 Java에서 상위 10개 정렬 알고리즘을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!