Python을 사용하여 행렬의 표준과 행렬식을 찾는 방법

scipy.linalg 함수에는 두 개의 매개변수가 제공되는 경우가 많습니다. 하나는 true인 경우 제한된 검사가 수행됩니다. 수행되는 경우 다른 유형은 overwrite_xxxx이며, 이는 계산 프로세스 중에 xxxx를 덮어쓸 수 있는지 여부를 나타냅니다. 단순화를 위해 나중에 a가 덮어쓰기 스위치를 제공한다고 설명하겠습니다. 이는 True일 때 매개변수 overwrite_a가 있음을 의미합니다. code>는 계산 프로세스를 재정의합니다. 제한된 확인 스위치가 제공되면 check_finite 매개변수가 제공된다는 의미입니다. scipy.linalg的函数中，往往会提供两种参数，其一是check_finite，当为True时将进行有限检查，另一类是overwrite_xxxx，表示xxxx在计算过程中是否可以被覆写。简洁起见，后文中说a提供覆写开关，就表示存在一个参数overwrite_a，当其为True时，a允许计算过程中被覆写；若说提供有限检查开关，则代表提供check_finite参数。

范数

在scipy.linalg中提供了函数norm用来求范数，其定义为

norm(a, ord=None, axis=None, keepdims=False, check_finite=True)

其中ord用于声明范数的阶 

ord	矩阵范数	向量范数
None	弗罗贝尼乌斯范数	2-范数
'fro'	弗罗贝尼乌斯范数	-
'nuc'	核范数	-
inf	max(sum(abs(a), axis=1))	max ⁡ ( ∣ a ∣ )
-inf	min(sum(abs(a), axis=1))	min ⁡ ( ∣ a ∣ )
0	-	sum(a!=0)
1	max(sum(abs(a), axis=0))
-1	min(sum(abs(a), axis=0))
2	2-范数(最大奇异值)
-2	最小奇异值

 若a为向量，若ord为非零整数，记作n nn，设a i a_iai为矩阵a aa中的元素，则矩阵的n nn范数为

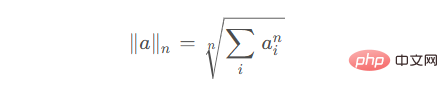
核范数又称“迹范数” (trace norm)，表示矩阵的所有奇异值之和。

Frobenius范数可定义为

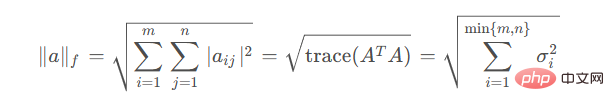
其实质是向量的2-范数在矩阵中的自然推广。

除了scipy.linalg之外，numpy.linalg中也提供了norm，其参数为

norm(x, ord=None, axis=None, keepdims=False)

其中order的可选参数与scipy.linalg中的norm函数相同。

行列式

在scipy.linalg中，行列式函数为det，其定义非常简单，除了待求矩阵a之外，就只有a的覆写开关和有限检查。

示例如下

import numpy as np
from scipy import linalg
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 0.0
a = np.array([[0,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 3.0

迹

scipy.linalg不提供trace函数，但是numpy提供，其定义为

umpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)

其中

• offset为偏移量，表示相对于主对角线的偏移

• axis1, axis2 表示坐标轴

• dtype

  Norm

  norm 함수는 scipy.linalg에 제공되어

>>> x = np.random.rand(3,3)
>>> print(x)
[[0.26832187 0.64615363 0.09006217]
 [0.63106319 0.65573765 0.35842304]
 [0.66629322 0.16999836 0.92357658]]
>>> np.trace(x)
1.8476361016546932

여기서 ord로 정의된 표준을 찾습니다. 는 노름의 순서를 선언하는 데 사용됩니다. 🎜 tr>max(sum(abs(a), 축=0))

ord	행렬 노름	벡터 노름 숫자
		td>
없음	프로베니우스 노름	2-노름
'fro'	프로베니우스 표준	-
'nuc'	핵 표준	-
inf	max(sum( abs(a), 축=1))	max ⁡ ( ∣ a ∣ )
-inf	min(sum(abs(a), axis=1))	min ⁡ ( ∣ a ∣ )
0	-	sum(a!=0)
1	td>
-1	min(sum(abs(a), axis=0))
2	2-노름(최대 특이값)
-2	최소 특이값

🎜 a가 벡터인 경우. >ord는 0이 아닌 정수이며 n nn으로 기록됩니다. a i a_iai를 행렬 a aa의 요소로 두고 행렬의 n nn 노름은 ​​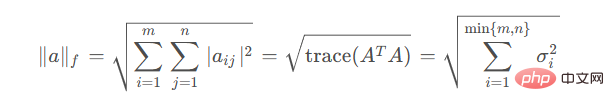🎜 🎜🎜🎜kernel 노름도, "추적 놈"으로 알려져 있으며, 행렬의 모든 특이값의 합을 나타냅니다. 🎜🎜Frobenius 표준은 다음과 같이 정의할 수 있습니다.🎜🎜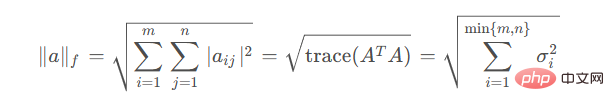🎜🎜핵심은 행렬에서 벡터의 2-노름을 자연스럽게 일반화하는 것입니다. 🎜🎜scipy.linalg 외에도 numpy.linalg는 매개변수가 🎜rrreee🎜인 norm도 제공합니다. 여기서 order는 선택 사항입니다. 의 매개변수는 scipy.linalg의 norm 함수와 동일합니다. 🎜

행렬

🎜 scipy.linalg에서 행렬식 함수는 det이고 정의는 매우 간단합니다. 단, 찾을 행렬은 a 외에도 재정의 스위치와 a에 대한 제한된 검사만 있습니다. 🎜🎜예제는 다음과 같습니다🎜rrreee

trace

🎜scipy.linalg는 trace 기능을 제공하지 않지만, numpy는 그렇습니다. 정의는 🎜rrreee🎜입니다. 여기서 🎜

• 🎜offset은 주 대각선을 기준으로 한 오프셋을 나타내는 오프셋입니다 🎜🎜
• 🎜axis1, axis2는 좌표축을 나타냅니다🎜🎜
• 🎜dtype은 출력 값을 조정하는 데 사용되는 데이터 유형입니다🎜🎜🎜rrreee

위 내용은 Python을 사용하여 행렬의 표준과 행렬식을 찾는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!