최근 광고주의 요구 변화와 관련 기술의 발전에 따라 컴퓨터 경제학 이론, 게임 이론 및 인공 지능 기술이 광고 경매 메커니즘 및 전달 전략에 점점 더 많이 적용되고 있습니다.
비즈니스 시나리오에서 의사결정 인텔리전스의 중요성은 점점 더 중요해지고 있습니다. 사용자가 보는 모든 제품 디스플레이, 판매자의 모든 광고 입찰, 플랫폼의 모든 트래픽 할당은 거대하고 복잡한 의사 결정 인텔리전스의 지원을 받습니다.
이러한 조치의 목표는 사용자 쇼핑 경험을 최적화하고, 광고 의사 결정 프로세스를 더욱 지능적으로 만드는 동시에 광고주와 미디어가 플랫폼에서 장기적인 번영을 달성할 수 있도록 하는 것입니다. 광고주는 제한된 자원 투자로 마케팅 효과를 극대화하고, 플랫폼은 더 나은 생태계를 구축하고자 합니다. 그러나 트래픽 환경의 복잡성, 다른 경쟁 광고에 의해 형성된 경쟁 환경, 그리고 광고 전략에 있어 입찰가, 타겟 그룹, 자원 위치, 배송 시간 등의 변수 조합의 엄청난 복잡성으로 인해 광고 전략이 계산되고 실행됩니다. 도전 가득한 최적의 광고 전략.
이러한 문제를 해결하는 방법은 무엇입니까? 혜택 극대화 목표는 어떻게 세분화됩니까? 의사결정 지능과 관련된 이러한 중요한 문제는 해당 분야의 연구자 및 실무자에게도 가장 큰 관심사입니다.
"디지털 지능 비즈니스 시나리오의 의사결정 지능"이라는 주제를 깊이 탐구하기 위해 Alimama Boxian Society와 Heart of Machines는 최근 북경대학교 Deng Xiaotie 교수, 중국과학원 Cai Shaowei 연구원, Alimama를 초청했습니다. CTO Zheng Bo 해당 분야의 선임 학자 및 전문가 3명이 일련의 주제를 공유했습니다.
다음은 Deng Xiaotie 교수, Cai Shaowei 연구원, Zheng Bo 선생님이 원래 의미를 바꾸지 않고 편집한 주제입니다.
Deng Xiaotie 교수: 계산 경제학의 몇 가지 최신 연구 발전
오늘은 1930년까지 거슬러 올라갈 수 있는 매우 역사적인 연구 분야인 계산 경제학을 간략하게 소개하겠습니다. 이후의 전산경제학은 다른 관점에서 출발하여 경제학을 계산으로 바꾸었습니다. 이전의 전산경제학은 계산을 통해 경제 연구를 한다는 것이었습니다.

컴퓨팅 관점에서 경제학을 생각할 때 몇 가지 주요 핵심 문제가 있습니다. 첫 번째는 최적화입니다. 기계 학습은 모두 최적화이며 여기에서 많은 최적화 시스템을 볼 수 있습니다. 최적화 다음에는 균형이라는 문제가 또 있습니다. 예전에 우리가 계산경제학을 할 때는 계획경제학의 관점에서 했는데요, 당시에는 개발도상국의 발전을 연구하는 학파도 있었습니다. 세계은행은 개발도상국을 위한 계획을 세우고 투입과 산출을 최적화하려는 아이디어를 개발하기 시작했습니다. 계산적 관점에서 평형을 계산하는 것은 매우 어려운 문제일 수 있으므로 계산 가능한 일반 평형이라는 개념이 등장했습니다.
최근에는 세상의 많은 것들이 균형을 이루고 있지 않기 때문에 점점 더 역동적인 시스템을 볼 수 있습니다. 균형의 가장 두드러진 장면은 가격 책정과 같은 경제 수준을 포함한 디지털 경제 활동입니다. 디지털 경제에서는 거래 데이터와 가격 변동이 매초 눈에 띕니다. 단순히 1년이 지난 경제 데이터를 집계하는 것이 아니라, 데이터의 변화를 명확하게 확인할 수 있습니다.
전산경제학의 전체 프레임워크에는 더 많은 것이 있습니다. 모든 경제 주체는 최적화해야 하며, 공동 게임의 고정점은 균형입니다. 플랫폼 역시 균형 게임을 펼칠 것이며, 특히 인터넷 광고 플랫폼에서는 광고주가 플랫폼에 와서 플랫폼과 미디어를 통해 광고를 배포합니다. 미디어의 경우 광고 위치를 제공하고 특정 유형의 사람들에게 자신의 매력을 활용하는 것이 필요합니다. 플랫폼에 있어서 우리가 생각해야 할 것은 어떻게 하면 모든 사람의 관심사를 더 잘 일치시킬 수 있는가 하는 것입니다. 중국 최대의 광고 플랫폼인 Alimama는 또한 게임 균형의 문제에 직면해 있습니다. 사회적 이익을 극대화하고 메커니즘 설계의 이점을 극대화하려면 모든 당사자의 이익을 조정해야 합니다.

최적화에 대해서는 세 가지 관점에서 이야기할 수 있습니다.
첫 번째는 경제지능의 특성화 문제입니다. 일부 환경의 제약 조건을 포함하여 기계 학습 방법을 사용하여 제약 조건을 계산하는 방법과 같은 많은 기계 학습 항목은 최적화 문제로 작성됩니다.
불완전한 정보 하에서는 알 수 없는 많은 조건이 있습니다. 게임 상대의 이익 함수는 무엇인지, 게임 상대의 전략 공간은 무엇인지, 게임 상대는 누구인지 등의 복잡한 사항을 고려할 수 없습니다. . , 불완전한 정보도 경제 활동을 설명하는 데 매우 중요합니다.
상대방의 이익 함수를 아는 경제인, 제약 조건 및 기타 다양한 정보와 같은 많은 가정은 불완전한 정보를 설명할 수 있습니다. 서로의 이익 기능에 대한 공통 지식이 있습니다. 우리는 분배를 알고 있습니다. 그런데 이 분포는 어디서 왔는가? 이것은 우리를 기계 학습의 영역으로 인도합니다. 플레이어는 왜 자신이 알고 있는 것을 서로에게 그리고 우리에게 말하는가? 이러한 점을 고려하면 계산 각도 측면에서 몇 가지 매우 합리적인 질문이 있습니다.
게임 역학, 이것이 전산경제학의 세 번째 단계입니다. 실물경제 경제학의 관점에서 보면 6,000년이 넘는 시간 동안 많은 활동들이 진화하고 발전해 왔으며, 모두가 균형에 도달할 때까지 천천히 게임을 하게 된다. 디지털 경제에서는 한꺼번에 균형을 이루는 것이 큰 도전이 될 것입니다.
광고 플랫폼 최적화는 알리마마가 하는 일입니다. 지금까지 어려운 컴퓨팅 작업에 대해 이야기를 많이 했는데 언제쯤 잘 할 수 있을까요? 단일 매개변수의 경우 기존 이론이 이를 뒷받침할 수 있지만 다중 매개변수를 달성하는 방법에 대한 이론상 기성 정의는 없습니다.
매우 중요한 점은 경제 시스템 전체가 확립되어 있지만 인터넷에서 경제학을 사용하면 정적이라는 큰 결함이 있다는 것입니다. 예를 들어, "Double Eleven" 프로모션은 많은 과제를 야기할 것입니다. 빨간 봉투의 가격을 어떻게 설계하고 알려진 시장 모델을 기반으로 이러한 것들을 구축하는지는 중요한 문제가 되었습니다. 오늘날의 계산경제학 과제: 하나는 대략적인 솔루션 최적화이고, 하나는 균형 계획이고, 다른 하나는 플랫폼 경쟁 역학입니다.

대략적인 계산은 매우 어렵습니다. 우리가 알고 있는 평형해는 최대 3분의 1까지 계산할 수 있고, 오류율은 최대 33%로 최적과 33% 차이가 나므로 평형 계산은 매우 어렵습니다. 정말 어렵습니다. 자동 설계 방법론과 숨겨진 상대 모델 학습이 이 영역의 프레임워크이며 모두 정보 용량과 관련됩니다.

다른 하나는 시장에서 알 수 없는 상대와 도박을 하는 것입니다. 우리는 적어도 두 회사를 고려하고 그들 사이의 게임을 디자인하기 위한 모델을 구축해야 합니다. 그것은 모두 단조롭고 모든 정보가 알려져 있지 않습니다. 알려진 정보를 바탕으로 시장 변동 및 가격 설계 변화를 살펴보고 이를 기반으로 암시적 함수의 최적화 모델을 설계하고 분석을 위해 머신러닝 방법을 사용합니다.
다자 인식의 순서는 게임의 인지 수준을 가져옵니다. 최근 몇 년간 여러 연구에서 1차 가격 경매가 2차 가격 경매보다 나은 이유에 대해 논의했습니다. Myerson은 모든 사람이 모든 사람의 가치 분포를 알고 있지만 실제로 대중의 지식은 모른다는 가정 하에 최적 경매 이론을 개발했습니다. 우리 자신의 연구를 또 다른 관점에서 고찰해 보면, 출발점은 사전 상식이 없으며, 확률론적 방법을 사용하여 마이어슨의 최적 경매 이론을 확립한다는 원래의 가정을 포기한다는 것입니다.
경매 균형에 대한 이러한 기본 가정이 없는 경우 최적의 솔루션이 어떻게 균형을 달성할 수 있습니까? 일반화된 단일가격 경매수익은 마이어슨과 동일함을 알 수 있다. 여기서는 최적 이익을 목표로 구매자가 발표한 가치 분포를 다루어야 합니다. 판매자가 설계한 Myerson 최적 수익은 일반화된 단일 가격 경매의 예상 경매 수익과 동일합니다.
최종 결론은 Myerson과 GFP가 동일하고 VCG보다 우수하지만 IID의 경우 동일하며 Symmetric BNE 및 GSP도 동일하다는 것입니다.
전산경제학에서 사용되는 또 다른 개념은 마르코프 게임(Markov game)입니다. 이는 역동적인 환경에서 게임, 특히 무한 라운드 게임을 해결하는 문제입니다. 우리는 세 가지 방향에서 문제를 다루었습니다. 첫째, 계산을 합리적으로 단순화하고 목표를 근사해로 제한했습니다. 둘째, 시간 할인율을 사용하여 무한 라운드 소득의 수렴을 보장했습니다. 셋째, 수학적 분석을 수행했습니다. 단계 요약은 여러 라운드의 전략 변경을 한 라운드의 변경으로 제한합니다. 이런 식으로 무한합산의 어려움을 극복할 수 있다.
마르코프 게임 적용 시 계산 난이도를 더욱 단순화시켰습니다. 합의 메커니즘 설계에 대한 명확한 Markov 보상 분석이 있으며 이는 좋은 이야기를 전달합니다. 메커니즘 설계의 규칙에 따르면 대부분의 사람들이 지지하는 것이 옳습니다. 그러나 다수의 지지가 경제적 안정을 보장하지 못한다는 사실이 나중에 밝혀졌습니다.
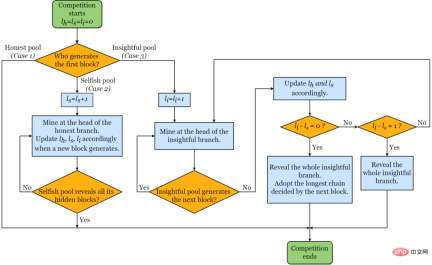
디지털 경제의 설계 과정에서 발생하는 문제에 대해 우리의 최신 작업은 통찰력 있는 마이닝 균형으로 극복할 수 있으며, 최적성을 달성하기 위한 장기적인 전략을 사용하고, 마지막으로 Markov 게임의 구조를 형성하여 Markov를 형성합니다. 보상 프로세스는 정직한 풀에서 이기적인 풀까지 인지 수준을 추가한 다음, 또 다른 수준을 넘어 비전 풀의 결과에 도달합니다.
마찬가지로 많은 인터넷 기업들은 정적인 것보다 역동적인 것을 다루어야 합니다. 또한 오늘날의 세계 경제는 더 이상 과거의 경제학이 아닙니다. 또한, 기계 학습 방법론과 게임 이론은 수학을 통해 밀접하게 통합됩니다. 이로써 우리는 정적인 경제학만 다룰 수 있는 상황을 극복하고, 역동적인 상황에 대처할 수 있는 수준으로 진화했습니다.
Cai Shaowei 연구원: 대규모 희소 조합 최적화 문제를 해결하기 위한 효율적인 방법
안녕하세요 여러분, 오늘 제가 공유하는 주제는 대규모 희소 조합 최적화를 위한 효율적인 방법입니다. 많은 의사 결정 문제의 핵심은 조합 최적화 문제와 관련되어 있으며, 사람들은 목표 최적화를 달성하기 위해 적절한 솔루션 조합을 선택하는 방법에 대해 매우 관심을 갖고 있습니다.
조합 최적화를 해결하는 방법에는 크게 두 가지가 있습니다. 하나는 휴리스틱 검색과 휴리스틱 구성을 포함하는 휴리스틱 방법입니다. 예를 들어 자주 사용되는 그리디 알고리즘은 일종의 휴리스틱 구성으로 간주할 수 있습니다. 휴리스틱(Heuristics); 다른 하나는 브랜드 앤 바운드(brand-and-bound)로 표현되는 정확한 알고리즘입니다.
휴리스틱 방법의 장점은 규모에 민감하지 않아 근사치를 사용하여 대규모 문제를 해결할 수 있다는 것입니다. 단점은 최적의 해리 해법이 어디까지인지 알 수 없는 경우가 많고, 최적의 해법이 있다는 것입니다. 예, 하지만 당신은 모릅니다. Branch And Bound가 완성되었습니다. 계산하고 중지하는 데 충분한 시간을 주면 최적의 솔루션을 찾고 그것이 최적의 솔루션임을 증명할 수 있습니다. 그러나 이 방법은 비용이 많이 들고 규모에 민감합니다. 왜냐하면 이러한 유형의 알고리즘은 기하급수적으로 폭발하고 대규모 문제에는 적합하지 않은 경우가 많기 때문입니다.
검색이든 구성이든 휴리스틱 알고리즘 프레임워크는 대부분 매우 간단합니다. 이는 주로 휴리스틱이 어떻게 설계되고 어떤 기준을 기반으로 해야 하는지에 따라 다릅니다. 분기 및 경계 방법은 주로 "경계"를 만드는 방법에 중점을 둡니다. 논문을 읽으면 경계를 더 엄격하게 만드는 방법이 솔루션 공간을 더 잘 정리할 수 있는 많은 Branch And Bound 논문을 찾을 수 있습니다.
나중에 생각해보니 이 둘을 합칠 수 있을까? 즉, 규모에 둔감할 뿐만 아니라 경계 기술도 추가할 수 있습니다. 전처리 방법을 사용하거나 휴리스틱스를 먼저 수행한 다음 Branch And Bound를 수행하고 휴리스틱스 결과를 초기 솔루션으로 사용할 수 있다고 생각하기 쉽습니다. 우리는 이와 관련하여 휴리스틱과 Branch And Bound의 중첩 반복이라는 새로운 접근 방식을 제안합니다.

간단히 말하면 이 방법은 먼저 대략적인 휴리스틱 해결을 수행하여 예비 결과를 찾습니다. 일반적으로 경계를 설정하려면 상한과 하한이 필요합니다. 휴리스틱에서는 대략적으로 하한을 구한 다음 상한에 대한 함수를 설계합니다. 문제가 상대적으로 크고 많은 요소를 포함한다고 가정하면 일부를 제거하여 문제를 더 작게 만들 수 있습니다. 그런 다음 좀 더 다듬고 휴리스틱 해결을 계속하면 하한이 향상될 수 있습니다. 이를 기반으로 알고리즘은 더 많은 경계를 수행하고 계속 중첩될 수 있습니다. 따라서 이 알고리즘은 준정확(semi-exact) 알고리즘이 되며, 특정 단계에서 문제 공간이 충분히 작다는 것을 발견하고 휴리스틱 해결이 필요하지 않지만 해결할 수 있기 때문에 이것이 최적의 솔루션임을 증명할 수 있습니다. 직접적이고 정확하게. 또한 최적해를 찾지 못한 경우 최적해 구간이 어디인지도 알 수 있습니다.

다음으로 이 방법을 설명하기 위해 두 가지 예를 들어보겠습니다.
첫 번째는 '최대 집단 문제'입니다. Clique는 그래프 이론의 매우 고전적인 개념으로, 그래프에는 점 사이의 모서리로 연결된 하위 그래프가 있는데 이를 Clique라고 합니다. 가중치를 부여하고 각 꼭지점에 가중치를 부여하면 최대가중파벌 문제는 총 가중치가 가장 큰 파벌을 찾는 문제이다. 아래 예에서는 각각 4개의 그룹과 3개의 그룹이 있으며, 이 그림에서 가장 큰 가중치 그룹은 세 그룹의 가중치가 더 큽니다.

이 프레임워크에 따라 이를 수행하려면 두 개의 하위 알고리즘이 필요합니다. 하나는 그룹에서 FindClique라고 하는 휴리스틱 솔루션이고 다른 하나는 ReduceGraph라고 하는 단순화 알고리즘입니다. FindClique를 사용하여 이전에 찾은 것보다 더 나은 파벌을 찾을 수 있습니다. 이 더 나은 그룹이 축소 그래프에 도달하면 우리가 아는 것은 가장 큰 그룹이 적어도 이 정도 크기라는 것입니다. 단순화도 이 단계에서 수행됩니다. 단순화 후 그래프가 비어 있으면 발견된 클러스터가 최적의 솔루션입니다. 비어 있지 않으면 일부 포인트를 줄이고 다시 돌아가 클러스터를 찾는 알고리즘을 조정할 수 있습니다. 여기서의 알고리즘은 반드시 고정된 알고리즘은 아니며 동적으로 변경될 수 있습니다.
우리 직업 중 하나는 다중 탐욕 알고리즘으로 이해할 수 있는 "구성 및 절단" 방법을 선택했습니다.

다중 그리디의 효과는 각각의 그리디 구성이 매우 빠르고 서로 다른 시작점에서 시작할 수 있으며 특정 구성 프로세스 중에 계산되면 현재 그룹을 아무리 확장할 수 없다는 것입니다. 이전에 찾은 그룹을 중지할 수 있습니다. 최종 목표는 이전보다 더 큰 그룹을 찾는 것입니다. 휴리스틱을 더 정교하게 만들어야 하는지, 순서를 어떻게 조정해야 하는지는 마치 양파를 특정 층까지 껍질을 벗긴 다음 다듬는 것과 같습니다. 더 나은 팀을 찾는 데 더 큰 초점을 맞추기 위해서입니다. 그래프를 더 이상 단순화할 수 없는 경우 Branch And Bound와 같은 정밀한 알고리즘을 사용할 수 있습니다. 우리의 방법에 따르면 그룹을 찾은 후 경계를 설정하고 일부 포인트를 버려야 합니다. 이 방법은 포인트가 전개할 수 있는 그룹의 크기를 추정하는 것이며 이를 해결하기 위한 다양한 솔루션이 있을 수 있습니다.
이 두 가지 경계 추정 기술은 단지 예일 뿐이며 이를 위해 서로 다른 기술을 사용할 수 있습니다. 실험적인 측면에서는 아래 표를 참조하여 FastWClq, LSCC+BMS, MaxWClq 등의 방법을 비교할 수 있습니다. 동일한 정확도를 달성하는 데 필요한 시간은 10배, 심지어 수백 배 이상 다릅니다.

두 번째 질문인 "그래프 색칠 문제"를 살펴보겠습니다. 그래프 색칠 문제는 그래프의 각 점을 색상으로 칠하는 것입니다. 인접한 두 점은 동일한 색상이 될 수 없습니다. 그래프 색칠 문제는 그래프를 색칠하는 데 사용할 수 있는 최소 색상 수에 대해 설명합니다. 그래프의 색상 번호라고 합니다. 그래프 색칠 문제는 특히 충돌 없이 자원을 할당하는 데 많은 응용이 가능합니다.
이 문제의 일반적인 아이디어는 동일합니다. 휴리스틱 솔루션에 일부 경계 기술을 더한 것입니다. 차이점은 그래프 색칠 문제에는 부분 집합이 필요하지 않기 때문에 "영원히 버려야 한다"는 개념이 없으며, 이 점은 반드시 색상. 여기서 축소는 그래프를 커널과 여백으로 분해하는 것입니다.
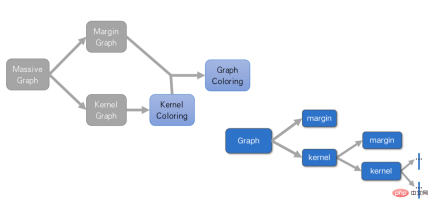
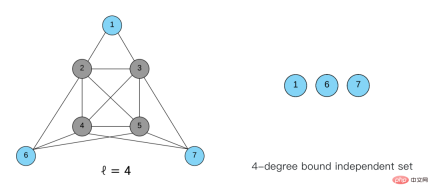
이 그래프에서 사용해야 하는 색상 수를 최소한 알고 있다면 여전히 독립 세트와 관련된 매우 간단한 규칙이 있습니다. 색상 하한(ℓ로 기록됨)이면 ℓ차 경계의 독립적인 집합을 찾을 수 있습니다. 이 독립 집합에 있는 점의 차수는 모두 ℓ보다 작으므로 ℓ차 경계라고 합니다. 그러한 독립적인 세트를 찾으면 안전하게 Margin으로 이동할 수 있습니다. 커널의 해를 찾으면 마진을 쉽게 통합할 수 있습니다. 커널이 최적의 해라면 그 조합도 최적의 해가 되어야 합니다. 이 규칙은 반복적으로 사용될 수 있습니다.

예를 들어 보겠습니다. 이 예에서는 4개의 회색 점이 커널입니다. 최소 4가지 색상이 필요합니다. 옆에 있는 세 점은 가장자리에 배치되어 있으므로 세 점의 각도는 4보다 작으므로 지금은 이 세 점을 옆으로 안전하게 이동하고 무시할 수 있습니다. 그러다가 나머지 하위 그래프를 분해할 수 없다는 사실을 발견했습니다. 이는 이미 매우 하드코어하며 직접 해결할 수 있습니다. 희소 그래프의 하드 코어는 일반적으로 크지 않으므로 솔루션을 위해 정확한 알고리즘을 고려할 수 있습니다. 코어를 찾으면 코어가 최소 4가지 색상을 사용하는 것으로 알려져 있습니다. 가장자리에 있는 점의 경우 각 점의 정도가 4 미만입니다. 어떻게 색상을 남길 수 있습니까? 시간. .
마지막까지 각 껍질의 여백을 유지해야 하며 레이어가 명확하게 표시되어야 합니다. 이는 첫 번째 질문과 약간 다릅니다. 이러한 에지 맵을 유지하려면 추가 데이터 구조를 사용해야 합니다. 이동할 수 없는 마지막 커널이 정확하게 해결된 후 역순 방법을 사용하여 먼저 마지막 마진을 병합하고 이전 규칙에 따라 최적성을 유지할 수 있습니다. , 가장자리를 병합하는 것은 여전히 최적입니다. 끝까지 되돌아가더라도 원본 이미지에 대한 솔루션도 최적이어야 합니다.
이 문제가 프레임화되면 남은 것은 하한과 상한을 찾는 방법을 고려하는 것뿐입니다. 알고리즘의 일반적인 아이디어는 다음과 같습니다. 처음에는 커널이 원본 이미지이고 하한을 찾기 위해 최대 클릭 알고리즘을 사용해야 하며, 가장자리를 벗겨낸 후 그리디 그래프 채색 알고리즘을 사용할 수 있습니다. 상한선을 찾으려면.

여기에는 실제로 세 가지 알고리즘이 사용됩니다. 실제로는 조합 펀칭 방법이 더 일반적이며, 특히 커널 컬러링의 경우 이미지가 상대적으로 클 경우 탐욕스럽거나 더 빠른 방법을 통해 수행할 수 있으며 최종적으로는 이를 수행하는 정확한 알고리즘이 될 수 있습니다. 프로세스 전반에 걸쳐 하한과 상한이 전역적으로 적용됩니다. 이 둘이 동일하면 중지할 수 있습니다.

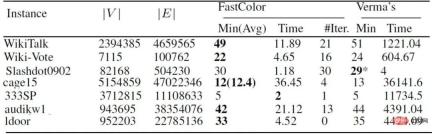
위 사진은 희박한 대형 이미지에서 효과가 더 좋은 것을 볼 수 있습니다. 144개 중 97개는 1분 안에 최적의 솔루션을 증명할 수 있습니다. 유사한 알고리즘에 비해 우리 알고리즘의 비교 시간도 더 빠릅니다. 상대적으로 희박한 큰 그래프에 대한 특별한 방법이 있어 문제를 빠르게 해결할 수 있습니다. 사람들은 수백만 개의 정점이 있는 NP 하드 문제를 해결하는 데 오랜 시간이 걸릴 것이라고 생각하곤 했습니다. 실제로 이러한 그래프가 크지만 특정 특성을 가지고 있으면 몇 초, 몇 분 안에 해결할 수 있습니다.
Alimama CTO Zheng Bo: 지속적으로 업그레이드되는 Alimama의 의사결정 지능 기술 시스템
안녕하세요 여러분, Alimama의 기술 리더로서 저는 지난 몇 년간 Alimama의 의사결정 지능 기술의 발전 과정을 여러분과 공유하겠습니다. 업계 관점 .
2007년에 설립된 알리마마는 온라인 광고 부문인 알리바바 그룹의 핵심 사업화 부서입니다. 알리마마는 10년 이상의 개발 끝에 '검색 광고 타오바오 익스프레스' 등 영향력 있는 제품을 탄생시켰으며, 2009년에는 디스플레이 광고와 Ad Exchange 광고 거래 플랫폼을 출시했고, 2014년에는 데이터 관리 플랫폼 다모판(Damopan)이 등장해 글로벌하게 시작했다. 2016년 마케팅.
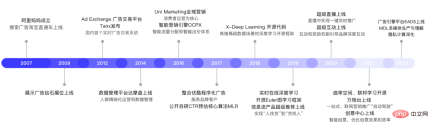
기술적인 관점에서 볼 때, 알리마마는 2015년과 2016년경 지능형 마케팅 엔진 OCPX부터 자체 개발한 CTR 예측 핵심 알고리즘 MLR 모델까지 모두 딥 러닝을 기반으로 했습니다. 방법은 끊임없이 진화하고 있습니다. 2018년에는 딥러닝 프레임워크인 X-Deep Learning이 오픈 소스로 공개되었습니다. 2019년에는 오일러 그래프 학습 프레임워크가 오픈 소스화되었으며, 정보 흐름 제품에 대한 슈퍼 추천도 출시되었습니다. "사람이 물건을 찾습니다"는 "상품이 사람을 찾습니다." 2020년부터 Alimama는 라이브 스트리밍 광고를 시작했으며, 더 자주 플레이되는 인터랙티브 게임 "Double Eleven" Stacking Cat과 같은 인터랙티브 인센티브 광고도 출시하기 시작했습니다. 곡률 공간 학습 프레임워크도 올해 오픈소스로 공개되었습니다.
2022년 알리마마는 광고 엔진 전체를 대대적으로 업그레이드했습니다. 광고 엔진 플랫폼 EADS와 멀티미디어 제작 및 이해 플랫폼 MDL은 모두 소비자 개인 정보 보호 측면에서 온라인이며 Alimama의 개인 정보 컴퓨팅 기술 역량은 중국 정보 통신 기술 아카데미(China Academy of Information and Communications Technology)의 인증을 받았습니다. 지난 15년 동안 Alimama의 발전을 되돌아보면 우리는 컴퓨터 광고에 종사하는 회사임을 알 수 있습니다.
알리마마의 장점은 무엇인가요? 매우 전문적인 전자상거래 분야에서 우리는 사용자와 전자상거래에 대해 매우 깊은 이해를 갖고 있으며, 전통적인 검색 및 추천 외에도 라이브 방송과 같은 디지털 비즈니스 시나리오도 매우 풍부합니다. 홍보, 상호 작용 및 새로운 형태. 또한 우리의 고객 기반은 세계 최대 규모 중 하나이며 수백만 명의 판매자가 Alimama 플랫폼의 광고주입니다. 이러한 고객은 운영에 대한 비즈니스 요구 사항 외에도 앵커, 전문가, 에이전트 및 서비스 제공업체와 같은 다양한 생태적 역할이 관련되어 있습니다. 그들은 다양한 역할로 이 플랫폼에서 활동합니다.

우리도 AI에 대한 연구를 많이 하고 있어요. 광고 장면 알고리즘 기술의 특징을 소개합니다. 위에서 본 것처럼 왼쪽의 역깔때기 구조는 검색이나 추천을 하는 많은 학생들에게 매우 친숙합니다. 광고의 이 부분은 광고 회상, 대략적인 정렬, 미세 정렬, 메커니즘 전략의 채점 등 검색 추천과 매우 유사합니다. 정보 검색 기술, 특히 TDM 매칭과 같은 회상 모델과 같은 대량의 AI가 관련된 기술은 모두 딥 러닝 기술을 사용합니다.
여기에는 의사결정 인텔리전스가 포함됩니다. 플랫폼에는 각각 고유한 게임 관계가 있는 많은 역할이 포함되어 있으므로 의사결정 인텔리전스는 다자간 관계와 최적화된 균형 사이에서 유용합니다. 사용자 경험, 트래픽 비용, 예상 수익, 예산 제어 및 도메인 간 통합이 모두 균형을 이루어야 합니다.
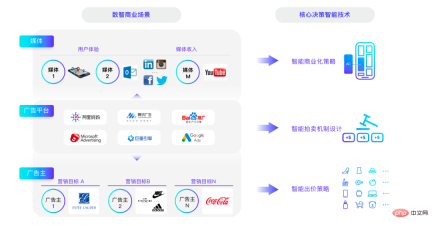
여기서는 대표적인 세 가지 게임 플레이어에 대해 이야기하겠습니다. 플랫폼에는 많은 플레이어가 있으며 미디어, 광고주, 광고 플랫폼이라는 세 가지 주요 범주가 있습니다.
이 세 부분의 핵심 기술은 다음과 같이 요약할 수 있습니다. 미디어 관점에서는 어떤 미디어 리소스가 광고주 관점에서 사용자 경험과 상업적 수익의 균형을 가장 잘 맞출 수 있는지, 무엇을 최적화해야 하는지, 마케팅 목표를 달성하는 방법에 중점을 둡니다. 최소한의 비용으로 . 그렇다면 광고 플랫폼의 가장 큰 목표는 무엇일까요? 장기적으로 광고 플랫폼의 하위 목표는 전체 플랫폼을 더욱 번영시키는 것입니다. 돈을 버는 것은 단기적인 문제일 뿐이며, 장기적으로 플랫폼을 번영시키는 것이 궁극적인 목표입니다. 플랫폼은 모든 당사자 간의 관계 균형을 유지해야 하며 모든 당사자의 플레이어가 플랫폼에서 플레이하는 것이 좋습니다.
광고 플랫폼의 최적화 목표에는 많은 메커니즘 설계가 포함됩니다. 오늘은 스마트 경매 메커니즘 설계, 스마트 입찰 전략, 스마트 상용화 전략의 세 가지 방향에 대해 간략하게 이야기하겠습니다. 이와 관련하여 지난 몇 년간 Alimama의 작업을 대중 과학 방식으로 모두가 논의할 수 있도록 하겠습니다.
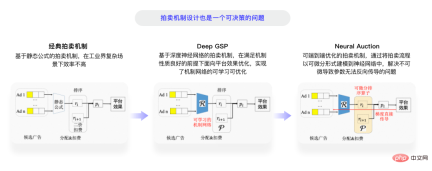
스마트 경매 메커니즘 디자인.
먼저 지능형 경매 메커니즘의 설계에 대해 이야기해 보겠습니다. 이는 매우 흥미로운 주제입니다. 많은 선배들과 전문가들이 노벨 경제학상을 수상했습니다. 우리가 말하는 고전적인 경매 메커니즘은 모두 1970년대 이전에 나타났습니다. 당시에는 온라인 광고가 아직 등장하지 않았으며 모두가 단일 경매 또는 정적 경매의 최적화에 대해 많은 연구를 했습니다. 이러한 메커니즘은 일반적으로 단일 대상이며 단일 경매에 사용됩니다.
광고 플랫폼이든 미디어이든 사용자 경험과 광고 수익의 균형이 필요합니다. 일반적인 업계 문제는 플랫폼에 관련된 비즈니스가 많으면 플랫폼 전략이 있을 수 있습니다. 이것은 또한 다중 목표 최적화입니다.
처음부터 트래픽 분배 및 가격 책정을 위해 GSP 또는 UGSP와 같은 고전적인 경매 이론이 사용되었습니다. 업계는 이 문제를 해결하기 위해 점차 딥 러닝으로 진화했습니다. 이러한 고전적인 알고리즘은 공식을 사용하여 플랫폼이 특정 목표를 위해 최적화하는 일부 매개 변수를 계산하며, 딥 러닝 도구를 사용하면 경매 메커니즘 자체의 설계도 의사 결정 문제를 해결하기 위한 알고리즘입니다. , 하지만 생산 의사결정 알고리즘도 의사결정 문제입니다.
3년 전, 우리는 딥러닝을 기반으로 하는 Deep GSP 경매 메커니즘을 설계했는데, 이는 이른바 좋은 본질인 플랫폼의 효과에 굶주린 메커니즘의 만족을 전제로 개선되었습니다. 메커니즘은 인센티브 호환성을 의미하며 광고주는 다른 사람들의 속내를 겪을 필요가 없습니다. 진정으로 원하는 것을 표현하면 입찰에 맞는 트래픽을 얻을 수 있습니다. Deep GSP는 인센티브 호환성 속성을 유지하고 원래의 정적 공식을 학습 가능한 딥 네트워크로 대체하는 작업의 첫 번째 단계입니다.
두 번째 단계에서는 학습 최적화를 통해 경매 메커니즘 네트워크의 많은 매개변수를 계산했습니다. 그러나 실제로는 매개변수 계산, 정렬, 광고 배포 프로세스 외에도 전체 프로세스에서 전체 시스템의 필수적인 부분입니다. 정렬 모듈과 같은 일부 모듈은 실제로 미분 가능하므로 딥 러닝 네트워크에서 이를 시뮬레이션하기 어렵습니다. 경매 메커니즘을 엔드 투 엔드로 설계하기 위해 경매 프로세스의 미분 가능 부분을 다음과 같이 모델링합니다. 전도를 사용하면 모델 훈련이 더 편리해집니다.
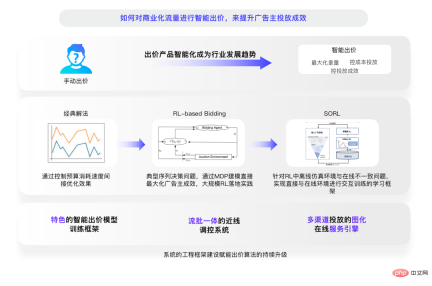
스마트 자동 입찰 전략.
다음으로, 광고주가 효과나 게임을 조정하기 위해 사용하는 가장 중요한 도구인 스마트 비딩 전략에 대해 이야기해보겠습니다. 중앙 집중식 배포는 수요를 표현할 수 없지만 광고 시나리오에서 이를 표현하는 방법이 있습니다. 입찰 제품은 세 가지 개발 단계로 나뉩니다.
원래의 클래식 솔루션은 가장 오래된 입찰 방법이기도 하며, 초기에는 업계에서 사용하는 효과가 더 원활하게 이루어지기를 바랍니다. PID와 유사한 제어 알고리즘은 효과가 제한적인 매우 간단한 알고리즘입니다.
2014년과 2015년 AlphaGo가 인간을 물리친 후 우리는 강화 학습의 힘을 보았습니다. 스마트 비딩(Smart Bidding)은 예산 주기 동안 이전 지출이 좋은지 아닌지가 후속 입찰 결정에 영향을 미치는 매우 일반적인 시퀀스 의사결정 문제이며, 이것이 강화 학습의 강점입니다. 강화학습 기반 입찰, MDP 모델링을 통해 강화학습을 직접 활용합니다.
세 번째 단계는 SORL 플랫폼으로 진화했는데, 강화학습에서 오프라인 시뮬레이션 환경과 온라인 환경의 불일치가 특징입니다. 우리는 엔지니어링 디자인과 알고리즘 디자인의 결합의 한 예인 온라인 환경에서 직접 대화형 학습을 진행합니다. SORL이 출시된 후 강화학습이 시뮬레이션 플랫폼에 크게 의존하는 문제를 대부분 해결했습니다.
기타 기술 기능에는 스마트 입찰 모델의 교육 프레임워크, 통합 흐름 및 배치 제어 시스템, 다중 채널 전달 그래픽 온라인 엔진을 포함한 엔지니어링 인프라 부분이 포함됩니다. 엔지니어링 시스템과 알고리즘도 똑같이 중요합니다. 거래 센터에 더 가까울수록 더 나은 피드백을 얻을 수 있으며, 스마트 비딩의 경우 엔지니어링 인프라가 발전할수록 광고주가 더 나은 성과를 거두는 데 도움이 될 수 있습니다. 결과.

스마트한 상용화 전략.
마지막으로 미디어와 관련된 스마트 상품화 전략에 대해 말씀드리겠습니다. 상품화 전략 최적화 측면에서 초기 시도는 광고 결과와 자연적 결과를 가중치로 통합한 후 이를 혼합하여 상황에 따라 선택하는 것이었습니다. 불합리한 상용화 메커니즘은 사용자 경험에 매우 해롭고 모든 사람들이 이 문제를 깨닫기 시작했습니다. 지난 1~2년 동안 딥 러닝 및 기타 기술의 발전으로 동적 디스플레이 전략이 점차 인기를 얻었습니다. 의사 결정 알고리즘을 최적화하여 사용자 경험과 상업적 수익의 균형을 맞추고 글로벌 트래픽과 사용자 경험의 균형을 맞출 수 있습니다.

일반적으로 Alimama는 세 가지 수준으로 나누어진 의사결정 지능형 시스템 다이어그램을 형성했습니다. 지능형 경매 메커니즘은 중간에 있는 다리이며 문제는 이를 통해 해결됩니다. 지능형 상용화 전략은 어떤 종류의 자원 경매가 가장 효율적이며 사용자 경험과 상업적 수입의 균형을 가장 잘 맞출 수 있습니까? 스마트 입찰 전략은 입찰 매개변수 최적화 및 강화 최적화를 통해 트래픽을 기반으로 정교한 입찰을 위한 의사 결정 프로세스입니다. 실제 환경을 기반으로 매개 변수를 학습하거나 Target CPX 및 Max Return과 같은 모델링 패러다임을 사용하여 최적화합니다.
현재의 다중 라운드 경매와 고주파 경매에 직면하여 많은 기본 이론을 더욱 깨뜨릴 필요가 있습니다. 기본 메커니즘의 이론적 돌파구에 관한 한 Deng 선생님은 이 분야의 전문가이시며 우리는 그 선생님과 함께 이 분야의 최첨단 연구를 수행할 수 있기를 기대합니다. 실제 엔지니어링 문제의 과제 관점에서 볼 때 실제 환경에서는 200ms 내에 결과가 반환되어야 하므로 효율성과 효과 사이에 어느 정도 균형이 필요합니다. 저는 오랫동안 업계에 근무하면서 이것을 경험했습니다.
광고 생태계의 최적화는 상대적으로 독립적입니다. 플랫폼의 궁극적인 목표는 생태계가 평화롭게 번성하고 발전하는 것입니다. 이것이 잘 이루어지면 생태계가 기대에 부응할 수 있을까요? 나는 둘 사이에 직접적인 방정식이 있을 수 없다고 생각합니다. 생태학적 최적화와 관련하여 아직 해결해야 할 이론적이고 실제적인 문제가 많이 있습니다. 앞으로 업계 친구들이 함께 논의하고 해결할 수 있기를 바랍니다.
지난 3년 동안 Alimama는 의사 결정 인텔리전스에 관해 최고의 국제 회의(NeurIPS, ICML, KDD, WWW 등)에서 약 20편의 논문을 발표했으며 베이징 대학교, 상하이 등 많은 대학과 협력했습니다. Jiao Tong University, 중국과학원, Zhejiang University의 연구 기관과의 협력을 통해 관련 결과가 업계와 학계의 광범위한 관심과 후속 조치를 받았습니다. 산업.
딥러닝에 비해 의사결정지능은 산업계나 학계에서 그다지 주목을 받지 못했는데, 매우 흥미롭고 유망한 이 분야에 대해 이번 기회를 통해 더 많이 알려드리고 싶습니다. 위 내용은 의사결정 지능에 대한 Alimama의 생각과 작업입니다. 업계 및 학계의 친구들과 공유하고 미래에 이에 대해 더 많이 논의하고 의사결정 지능에 대한 이론적 연구에서 획기적인 발전을 이루기 위해 노력할 수 있기를 바랍니다. 업계의 실제 응용.
위 내용은 디지털 인텔리전스 사업 분야는 의사결정 인텔리전스 기술의 과제에 어떻게 대응합니까? 세 명의 전문가의 답변의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 Microsoft Work Trend Index 2025는 작업장 용량 변형을 보여줍니다Apr 24, 2025 am 11:19 AM
Microsoft Work Trend Index 2025는 작업장 용량 변형을 보여줍니다Apr 24, 2025 am 11:19 AMAI의 빠른 통합으로 악화 된 직장의 급성장 용량 위기는 점진적인 조정을 넘어 전략적 변화를 요구합니다. 이것은 WTI의 발견에 의해 강조됩니다. 직원의 68%가 작업량으로 어려움을 겪고 BUR로 이어
 AI가 이해할 수 있습니까? 중국의 객실 논쟁은 아니오라고 말하지만 맞습니까?Apr 24, 2025 am 11:18 AM
AI가 이해할 수 있습니까? 중국의 객실 논쟁은 아니오라고 말하지만 맞습니까?Apr 24, 2025 am 11:18 AMJohn Searle의 중국 방 주장 : AI 이해에 대한 도전 Searle의 사고 실험은 인공 지능이 진정으로 언어를 이해할 수 있는지 또는 진정한 의식을 가질 수 있는지 직접 의문을 제기합니다. Chines를 무시하는 사람을 상상해보십시오
 중국의 '스마트'AI 조수는 Microsoft Recall의 개인 정보 결함을 반향합니다Apr 24, 2025 am 11:17 AM
중국의 '스마트'AI 조수는 Microsoft Recall의 개인 정보 결함을 반향합니다Apr 24, 2025 am 11:17 AM중국의 기술 거대 기업은 서부에 비해 AI 개발 과정에서 다른 과정을 차트하고 있습니다. 기술 벤치 마크 및 API 통합에만 초점을 맞추는 대신 "스크린 인식"AI 비서 우선 순위를 정합니다.
 Docker는 AI 모델 및 MCP 도구에 친숙한 컨테이너 워크 플로를 제공합니다.Apr 24, 2025 am 11:16 AM
Docker는 AI 모델 및 MCP 도구에 친숙한 컨테이너 워크 플로를 제공합니다.Apr 24, 2025 am 11:16 AMMCP : AI 시스템이 외부 도구에 액세스 할 수 있도록 권한을 부여합니다 MCP (Model Context Protocol)를 사용하면 AI 애플리케이션이 표준화 된 인터페이스를 통해 외부 도구 및 데이터 소스와 상호 작용할 수 있습니다. MCP를 통해 MCP는 인류에 의해 개발되고 주요 AI 제공 업체가 지원하는 언어 모델 및 에이전트가 사용 가능한 도구를 발견하고 적절한 매개 변수로 전화 할 수 있습니다. 그러나 환경 충돌, 보안 취약점 및 일관되지 않은 교차 플랫폼 동작을 포함하여 MCP 서버 구현에는 몇 가지 과제가 있습니다. Forbes 기사 "Anthropic의 모델 컨텍스트 프로토콜은 AI 에이전트 개발의 큰 단계입니다."저자 : Janakiram MSVDocker는 컨테이너화를 통해 이러한 문제를 해결합니다. Docker Hub Infrastructure를 구축했습니다
 6 억 달러 규모의 스타트 업을 구축하기 위해 6 개의 AI Street-Smart 전략 사용Apr 24, 2025 am 11:15 AM
6 억 달러 규모의 스타트 업을 구축하기 위해 6 개의 AI Street-Smart 전략 사용Apr 24, 2025 am 11:15 AM최첨단 기술을 활용하고 비즈니스 통제력을 발휘하여 통제력을 유지하면서 수익성이 높고 확장 가능한 회사를 창출하는 비전 기업가가 사용하는 6 가지 전략. 이 안내서는
 Google 사진 업데이트 모든 사진에 대한 멋진 Ultra HDR 잠금 해제Apr 24, 2025 am 11:14 AM
Google 사진 업데이트 모든 사진에 대한 멋진 Ultra HDR 잠금 해제Apr 24, 2025 am 11:14 AMGoogle 사진의 새로운 Ultra HDR 도구 : 이미지 향상을위한 게임 체인저 Google Photos는 강력한 Ultra HDR 변환 도구를 도입하여 표준 사진을 활기차고 높은 동기 범위 이미지로 변환했습니다. 이 향상은 사진가 a
 Descope는 AI 에이전트 통합을위한 인증 프레임 워크를 구축합니다Apr 24, 2025 am 11:13 AM
Descope는 AI 에이전트 통합을위한 인증 프레임 워크를 구축합니다Apr 24, 2025 am 11:13 AM기술 아키텍처는 새로운 인증 문제를 해결합니다 에이전트 Identity Hub는 문제를 해결합니다. 많은 조직이 AI 에이전트 구현을 시작한 후에 만 기존 인증 방법이 기계 용으로 설계되지 않았다는 것을 발견 한 후에 만 발견합니다.
 Google Cloud 다음 2025 및 현대 작업의 연결된 미래Apr 24, 2025 am 11:12 AM
Google Cloud 다음 2025 및 현대 작업의 연결된 미래Apr 24, 2025 am 11:12 AM(참고 : Google은 회사 인 Moor Insights & Strategy의 자문 고객입니다.) AI : 실험에서 Enterprise Foundation까지 Google Cloud Next 2025는 실험 기능에서 엔터프라이즈 기술의 핵심 구성 요소까지 AI의 진화를 보여주었습니다.


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

Atom Editor Mac 버전 다운로드
가장 인기 있는 오픈 소스 편집기

MinGW - Windows용 미니멀리스트 GNU
이 프로젝트는 osdn.net/projects/mingw로 마이그레이션되는 중입니다. 계속해서 그곳에서 우리를 팔로우할 수 있습니다. MinGW: GCC(GNU Compiler Collection)의 기본 Windows 포트로, 기본 Windows 애플리케이션을 구축하기 위한 무료 배포 가능 가져오기 라이브러리 및 헤더 파일로 C99 기능을 지원하는 MSVC 런타임에 대한 확장이 포함되어 있습니다. 모든 MinGW 소프트웨어는 64비트 Windows 플랫폼에서 실행될 수 있습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

WebStorm Mac 버전
유용한 JavaScript 개발 도구







