그래프 머신러닝은 어디에나 있으며 Transformer를 사용하여 GNN 제한을 완화합니다.

오늘날 우리 생활에서 그래프의 예로는 Twitter, Mastodon과 같은 소셜 네트워크와 논문과 저자를 연결하는 모든 인용 네트워크, 분자, UML 다이어그램과 같은 지식 그래프, 백과사전, 하이퍼링크가 있는 웹사이트, 표현 등이 있습니다. 구문 트리를 3D 그리드에 연결하면 그래프가 어디에나 있다고 말할 수 있습니다.

최근 Hugging Face 연구 과학자인 Clémentine Fourrier는 "그래프 머신러닝 소개"라는 기사에서 오늘날의 유비쿼터스 그래프 머신러닝을 소개했습니다. 그래픽이란 무엇입니까? 그래프를 사용하는 이유는 무엇입니까? 그래프를 가장 잘 표현하는 방법은 무엇입니까? 사람들은 그래프를 통해 어떻게 학습하나요? 클레멘틴 푸리에(Clémentine Fourrier)는 그래프가 관계로 연결된 항목에 대한 설명이라고 지적했습니다. 그 중 사전 신경망 방법부터 그래프 신경망까지 여전히 그래프에 대한 학습 방법이 널리 사용됩니다.

또한 최근 일부 연구자들은 Transformer를 그래프에 적용하는 것을 고려하기 시작했습니다. Transformer는 확장성이 좋고 GNN의 한계를 일부 완화할 수 있으며 전망은 매우 밝습니다.

1 다이어그램은 관계로 연결된 항목에 대한 설명입니다.

기본적으로 다이어그램은 관계로 연결된 항목에 대한 설명입니다. 그래프(또는 네트워크)의 항목은 노드(또는 정점)라고 하며 가장자리(또는 링크)로 연결됩니다. 예를 들어 소셜 네트워크에서 노드는 사용자이고 가장자리는 사용자 간의 분자 연결이고 노드는 원자이며 가장자리는 분자 결합입니다.

• 유형화된 노드 또는 유형화된 가장자리가 있는 그래프를 이종 그래프라고 합니다. 예를 들어 인용 네트워크의 항목은 유형화된 노드가 있는 논문 또는 저자일 수 있지만 XML 그래프의 관계는 유형화된 가장자리를 나타낼 수 없습니다. 토폴로지만으로도 추가 정보가 필요합니다.
• 그래프는 방향이 지정될 수도 있습니다(예: 팔로어 네트워크, A가 B를 따른다고 해서 B가 A를 따른다는 의미는 아님). 방향이 지정되지 않을 수도 있습니다(예: 분자, 원자 간의 관계는 양방향임). Edge는 서로 다른 노드 또는 노드를 자신과 연결할 수 있지만(Self-Edge) 모든 노드를 연결할 필요는 없습니다

보시다시피 데이터를 사용할 때 먼저 동종/이종을 포함한 최적의 표현을 고려해야 합니다. , 방향성/무방향성 등

그래프 수준에서 주요 작업은 다음과 같습니다.

• 그래프 생성, 새로운 합리적 분자를 생성하기 위한 약물 발견
• 그래프 진화, 즉 어떻게 변화할지 예측하기 위한 그래프 제공 물리학에서 시스템의 진화를 예측하는 데 사용할 수 있는 시간 진화
• 분자의 독성 예측과 같은 그래프 수준의 예측, 분류 또는 회귀 작업

일반적으로 노드 계층이 예측입니다. Alphafold와 같은 노드 속성의 노드 속성 예측을 사용하여 분자의 전체 그래프를 바탕으로 원자의 3D 좌표를 예측하고 이에 따라 분자가 3D 공간에서 접히는 방식을 예측하는 것은 어려운 생화학 문제입니다.

Edge 예측에는 Edge 속성 예측과 누락 Edge 예측이 포함됩니다. 가장자리 속성 예측은 약물 쌍의 부작용을 고려하여 약물 부작용을 예측하는 데 도움이 됩니다. 누락된 가장자리 예측은 그래프의 두 노드가 관련되어 있는지 예측하는 추천 시스템에 사용됩니다.

하위 그래프 수준에서는 커뮤니티 탐지 또는 하위 그래프 속성 예측을 수행할 수 있습니다. 소셜 네트워크는 커뮤니티 감지를 사용하여 사람들이 어떻게 연결되어 있는지 확인할 수 있습니다. 하위 그래프 속성 예측은 예상 도착 시간을 예측하는 데 사용할 수 있는 Google 지도와 같은 여행 일정 시스템에서 자주 사용됩니다.

특정 그래프의 발전을 예측하는 경우 학습, 검증, 테스트를 포함한 변환 설정의 모든 작업을 동일한 그래프에서 수행할 수 있습니다. 그러나 단일 그래프에서 학습, 평가 또는 테스트 데이터 세트를 생성하는 것은 쉽지 않으며, 유도 설정이라고 하는 서로 다른 그래프(별도의 학습/평가/테스트 분할)를 사용하여 많은 작업이 수행됩니다.

그래프 처리 및 작업을 표현하는 두 가지 일반적인 방법이 있습니다. 모든 모서리 집합(모든 노드 집합으로 보완될 수 있음) 또는 모든 노드 간의 인접 행렬입니다. 그 중 인접행렬은 어떤 노드가 다른 노드에 직접 연결되어 있는지를 나타내는 정사각행렬(노드크기×노드크기)이다. 희소 인접 행렬을 사용하면 대부분의 그래프가 조밀하게 연결되지 않기 때문에 계산이 더 어려워집니다.

그래프는 "시퀀스"(예: 텍스트 및 오디오) 또는 "정렬된 그리드"(예: 이미지 및 비디오)보다 더 복잡한 토폴로지로 인해 ML에서 사용되는 일반적인 개체와 매우 다릅니다. 비록 목록으로 표현될 수 있지만 또는 행렬이지만 이 표현은 정렬된 개체로 간주될 수 없습니다. 즉, 문장의 단어를 뒤섞으면 새 문장이 만들어지고, 이미지를 뒤섞고 열을 재배열하면 새 이미지가 만들어집니다.

그림: Hugging Face 로고와 중단된 Hugging Face 로고는 완전히 다른 새 이미지입니다

그러나 그림의 경우는 그렇지 않습니다. 그림의 가장자리 목록을 씻어 내면 또는 인접 행렬의 열에도 여전히 동일한 그래프입니다.

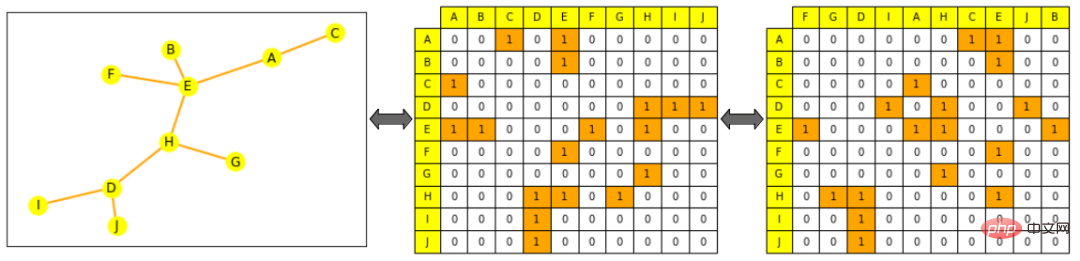
그림 참고: 왼쪽은 작은 그림이고, 노란색은 노드를 나타내고, 주황색은 가장자리를 나타냅니다. 중앙 그림의 인접 행렬, 열과 행은 노드 알파벳 순서로 정렬됩니다. 노드 A의 행 (첫 번째 행) E와 C에 연결되어 있음을 알 수 있습니다. 오른쪽 그림은 인접 행렬을 방해합니다(열은 더 이상 알파벳 순서가 아님). 이는 여전히 그래프의 유효한 표현입니다.

2 ML의 그래프 표현으로

기계 학습을 사용하여 그래프로 작업하는 일반적인 프로세스는 먼저 노드, 에지 또는 프로젝트에 대한 의미 있는 표현을 생성하는 것입니다. 전체 그래프는 특정 작업 요구 사항에 따라 달라지며 대상 작업에 대한 예측기를 교육합니다. 다른 패턴과 마찬가지로 객체의 수학적 표현을 제한하여 유사한 객체와 수학적으로 유사하도록 할 수 있습니다. 그러나 이 내에서는 그래프 ML에서 유사성을 엄격하게 정의하기가 어렵습니다. 예를 들어 두 노드가 동일한 레이블을 가질 때 또는 동일한 이웃을 가질 때 더 유사한가요?

아래에 표시된 것처럼 이 기사에서는 노드 표현 생성에 중점을 둡니다. 노드 수준 표현이 있으면 에지 또는 그래프 수준 정보를 얻을 수 있습니다. 에지 수준 정보의 경우 노드 쌍을 연결하거나 그래프 수준 정보의 경우 점 곱셈을 수행할 수 있으며, 평균화, 합계 등을 포함하여 모든 노드 수준으로 표시되는 연결된 텐서에 대해 전역 풀링을 수행할 수 있습니다. 그러나 여전히 전체 그래프에 대한 정보가 부드러워지고 손실됩니다. 재귀 계층적 컬렉션이 더 적합하거나 그래프의 다른 모든 노드에 연결된 더미 노드를 추가하고 이를 전체 그래프 표현으로 나타낼 수 있습니다.

사전 신경 방법

단순히 엔지니어링 기능 사용

신경망 이전에는 그래프와 관심 항목이 기능의 조합으로 작업별 방식으로 표현될 수 있었습니다. 오늘날 이러한 기능은 여전히 ​​데이터 증대 및 준지도 학습에 사용되며, 보다 정교한 기능 생성 방법이 존재하지만 작업에 따라 이러한 기능을 네트워크에 제공하는 가장 좋은 방법을 찾는 것이 중요합니다.

노드 수준 기능은 구조 기반 정보뿐만 아니라 중요도에 대한 정보도 제공하고 결합할 수 있습니다.

노드 중심성은 그래프에서 노드의 중요도를 측정하는 데 사용할 수 있으며, 수렴할 때까지 각 노드의 이웃 중심성을 합산하여 재귀적으로 계산하거나 노드 사이의 최단 거리를 측정하여 재귀적으로 계산할 수 있으며 노드 정도는 해당 숫자입니다. 직접 이웃의 클러스터링 계수는 노드의 이웃이 어떻게 연결되어 있는지 측정합니다. Graphlets 정도 벡터 계산은 주어진 노드에 루트가 있는 서로 다른 그래프의 수를 계산합니다. 여기서 그래프는 지정된 수의 연결된 노드를 사용하여 생성될 수 있습니다.

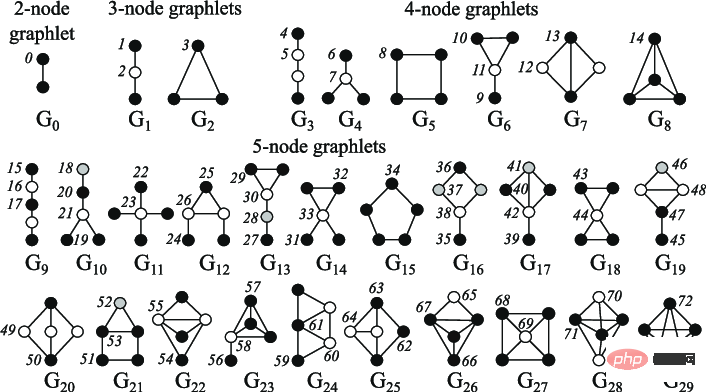
그림 참고: 2~5노드 작은 그래프

에지 수준 기능은 두 노드 간의 최단 거리, 공통 이웃 및 Katz를 포함하여 노드 연결에 대한 자세한 정보로 보완됩니다. 인덱스(두 노드 사이의 특정 길이의 가능한 경로 수 - 인접 행렬에서 직접 계산할 수 있음)

그래프 수준 기능에는 그래프 유사성과 특이성에 대한 상위 수준 정보가 포함되어 있습니다. 여기서 하위 그래프 수는 계산 비용이 많이 들지만 하위 그래프 모양에 대한 정보를 제공합니다. 핵심 방법은 다양한 "bag-of-nodes" 방법(bag-of-words와 유사)을 통해 그래프 간의 유사성을 측정합니다.

Walk 기반 방법

Walk 기반 방법은 무작위 보행으로 노드 i에서 노드 j를 방문할 확률을 사용하여 유사성 측정을 정의합니다. 이러한 방법은 로컬 정보와 전역 정보를 결합합니다. 예를 들어, 이전에 Node2Vec은 임베딩을 계산하기 위해 문장에서 단어를 수행하는 것처럼 건너뛰기 그램을 사용하여 이러한 보행을 처리하여 그래프 노드 간의 무작위 보행을 시뮬레이션했습니다.

이러한 방법은 PageRank 방법의 계산 속도를 높이는 데도 사용할 수 있습니다. 이 방법은 각 노드에 다른 노드와의 연결을 기반으로 중요도 점수를 할당합니다(예: 액세스 빈도를 평가하기 위한 무작위 이동). 그러나 위의 방법에도 특정 제한 사항이 있습니다. 새로운 노드를 삽입할 수 없고 노드 간의 구조적 유사성을 잘 포착할 수 없으며 추가된 기능을 사용할 수 없습니다.

3 그래프 신경망은 그래프를 어떻게 처리하나요?

신경망은 보이지 않는 데이터로 일반화할 수 있습니다. 앞서 언급한 표현 제약 조건을 고려할 때 좋은 신경망은 그래프를 어떻게 처리해야 할까요?

두 가지 방법이 아래에 나와 있습니다.

• 은 순열 불변입니다.

• 방정식: f(P(G))=f(G)f(P(G))= f(G ), 여기서 f는 네트워크, P는 순열 함수, G는 그래프
• 설명: 네트워크를 통과한 후 그래프의 표현과 배열은 동일해야 합니다

• 은 순열 등변량

• 방정식: P(f(G))=f(P(G))P(f(G))=f(P(G)), 여기서 f는 네트워크이고 P는 순열입니다. 함수이고 G는 그래프입니다

• 설명: 노드를 네트워크에 전달하기 전에 노드를 순열하는 것은 해당 표현을 순열하는 것과 동일해야 합니다

일반적인 신경망은 RNN 또는 CNN과 같은 순열 불변이 아닙니다. 그래서 새로운 아키텍처 — —그래프 신경망이 도입되었습니다(처음에는 상태 기반 기계로).

A GNN은 연속적인 레이어로 구성됩니다. GNN 레이어는 이전 레이어(메시지 전달)의 이웃과 자체 표현의 조합으로 노드를 나타내며, 종종 일부 비선형성을 추가하기 위해 활성화가 추가됩니다. 다른 모델과 비교하여 CNN은 고정된 이웃 크기(슬라이딩 윈도우를 통해) 및 순서(비순열 등분산)를 갖는 GNN으로 간주될 수 있는 반면 위치 임베딩이 없는 Transformer는 완전히 연결된 입력 그래프에서 GNN으로 간주될 수 있습니다.

집계 및 메시징

합산 및 평균화와 같은 이전의 유사한 클러스터링 방법에는 다음이 포함됩니다.

• 노드 이웃에 대한 그래프 컨볼루션 네트워크 정규화된 표현 평균화
• Graph Isomorphism Networks, 노드 이웃 표현의 합에 MLP를 적용하여 집계 표현.
• 집계 선택: 일부 집계 기술(특히 평균/최대 세트)은 유사한 노드의 서로 다른 노드 이웃 표현을 구별하는 세분화된 표현을 생성하는 데 실패합니다. 예를 들어 평균 세트를 사용하면 이웃이 있습니다. 4개 노드 중 1개 노드는 1, 1, -1, -1로 표시되고 평균은 0으로 -1, 0, 1로 표시되는 3개 노드만 있는 이웃과 별반 다르지 않습니다.

• GNN 모양 및 과도하게 평활화 문제

  각 새 레이어에서 노드 표현에는 점점 더 많은 노드가 포함됩니다. 노드는 직접적인 이웃의 집합인 첫 번째 계층을 통과합니다. 두 번째 레이어를 통해 여전히 인접한 이웃의 집합이지만 이제 표현에는 첫 번째 레이어의 이웃도 포함됩니다. n 수준 이후 모든 노드의 표현은 거리 n에 있는 모든 이웃의 집합이 되며, 따라서 직경이 n보다 작으면 전체 그래프의 집합이 됩니다.

  네트워크 레이어가 너무 많으면 각 노드가 전체 그래프의 집합이 될 위험이 있습니다(그리고 노드 표현이 모든 노드에 대해 동일한 표현으로 수렴됩니다). 이를 과잉 평활화 문제라고 하며, 해결 방법:

  • GNN을 각 노드가 전체 네트워크로 근사되지 않도록 충분히 작은 수의 레이어로 확장합니다(먼저 그래프의 직경과 모양을 분석하여)
  • 복잡성을 높입니다.
  • 메시지를 처리하기 위해 메시지가 아닌 전달 레이어를 추가합니다(예: 간단한 MLP)
  • 건너뛰기 연결 추가

  과도하게 평활화하는 문제는 그래프 ML의 중요한 연구 영역입니다. 이는 Transformers가 다른 모델에서 입증된 것처럼 GNN이 확장되는 것을 방지합니다.

  Graph Transformers

  위치 인코딩 레이어가 없는 Transformer는 순열 불변이며 Transformer도 확장성도 좋아 최근 연구자들은 Transformer를 그래프에 적용하는 것을 고려하기 시작했습니다. 대부분의 방법은 최고의 특징과 그래프를 표현하는 가장 좋은 방법을 찾고, 이 새로운 데이터에 적응하도록 주의를 바꾸는 데 중점을 둡니다.

  아래는 스탠포드 대학의 오픈 그래프 벤치마크에서 최고 수준 또는 근접한 결과를 달성하는 몇 가지 방법을 보여줍니다.

  • 그래프 대 시퀀스 학습을 위한 그래프 변환기는 노드가 다음과 같은 그래프 변환기를 소개합니다. 임베딩과 위치 임베딩의 연결로 표현되며 노드 관계는 둘 사이의 최단 경로를 나타내며 둘을 하나의 관계로 결합하여 자기 집중을 향상시킵니다.
  • SAN(Spectral Attention Networks)을 도입하여 Spectral Attention을 사용하여 그래프 변환기를 다시 생각합니다. 이러한 노드 기능은 키 및 쿼리로 사용되는 학습된 위치 인코딩(라플라시안 기능 벡터/값에서 계산)과 결합되며, Attention 값은 에지 기능입니다.
  • GRPE: Relative Positional Encoding for Graph Transformer는 그래프 레벨 위치 인코딩과 노드 정보, 에지 레벨 위치 인코딩과 노드 정보를 결합한 그래프 상대 위치 인코딩 Transformer를 소개하며, 두 가지를 주목적으로 결합한 중간은 다이어그램.
  • Graph Convolution을 대체하는 Global Self-Attention은 노드와 에지를 별도로 내장하고 수정된 Attention으로 집계하는 아키텍처인 Edge Augmented Transformer를 도입합니다.
  • Do Transformers는 OGB에서 1위를 차지했던 Microsoft의 Graphormer를 소개합니다. 아키텍처는 노드 기능을 어텐션의 쿼리/키/값으로 사용하고 어텐션 메커니즘의 중심성, 공간 및 에지 인코딩과 표현을 결합합니다.

  최근 연구 "Pure Transformers are Powerful Graph Learners"는 TokenGT 방법을 도입하여 입력 그래프를 일련의 노드 및 에지 임베딩으로 표현합니다. 즉, 직교 노드 식별자와 훈련 가능한 유형 식별자를 사용하여 위치 임베딩 없이 증강을 수행합니다. 이 시퀀스를 Transformer에 입력으로 제공합니다. 이 접근 방식은 매우 간단하면서도 동시에 매우 효율적입니다.

  

  논문 주소: https://arxiv.org/pdf/2207.02505.pdf

  또한 "Recipe for a General, Powerful, Scalable Graph Transformer" 연구에서 다른 방법 차이점은 모델이 아니라 메시지 전달 네트워크를 선형(원격) 변환기와 결합하여 하이브리드 네트워크를 쉽게 만들 수 있는 GraphGPS라는 프레임워크를 도입한다는 것입니다. 프레임워크에는 위치 및 구조적 인코딩(노드, 그래프, 에지 수준), 기능 확대, 랜덤 워크 등을 계산하기 위한 여러 도구도 포함되어 있습니다.

  

  논문 주소: https://arxiv.org/abs/2205.12454

  트랜스포머를 그래프에 사용하는 것은 아직 초기 단계이지만 현재로서는 전망이 매우 밝습니다. 더 크거나 밀도가 높은 그래프로 확장하거나 과도하게 평활화하지 않고 모델 크기를 늘리는 등 GNN의 일부 제한 사항을 완화할 수 있습니다.

위 내용은 그래프 머신러닝은 어디에나 있으며 Transformer를 사용하여 GNN 제한을 완화합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!