Java에서 이진 트리의 가장 가까운 공통 조상을 찾는 방법

아이디어 1: 먼저 이 트리가 이진 검색 트리라고 가정합니다

우선 이진 검색 트리가 무엇인지에 대한 보충 설명을 추가해 보겠습니다.

이진 검색 트리에서 각 노드의 왼쪽 하위 트리 값 in은 모두 그보다 작고, 오른쪽 하위 트리의 값은 모두 그보다 큽니다. 따라서 이진 검색 트리의 순차 순회는 순서가 지정된 데이터 집합입니다.

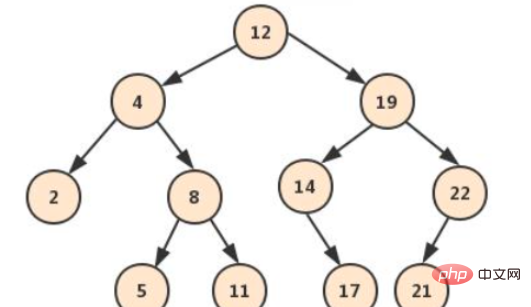
위 트리의 경우 p q의 가장 최근 공통 조상이 필요하다고 가정합니다.

다음 상황은 다음과 같습니다.

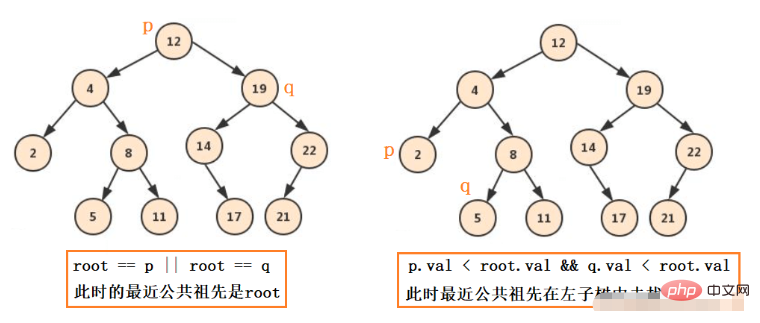
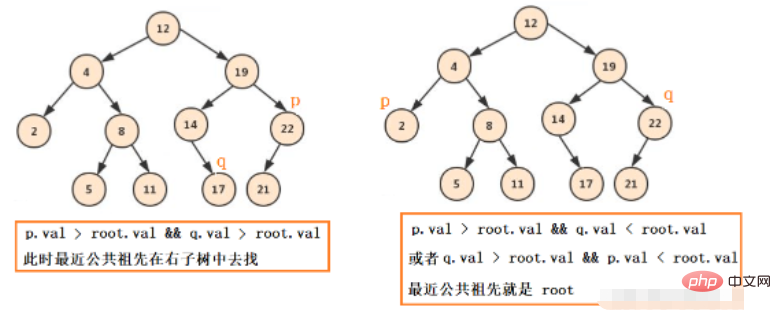
일반적인 이진 트리의 경우 다음과 같은 상황에 지나지 않습니다. pq는 왼쪽에, pq는 오른쪽에, pq는 왼쪽에, 1은 위에 있습니다. 오른쪽, pq에는 루트 노드가 있습니다.

그래서 왼쪽 하위 트리와 오른쪽 하위 트리로 재귀적으로 이동하여 p q 노드의 공통 조상을 찾으면 노드를 찾지 못하면 빈 값을 반환합니다.

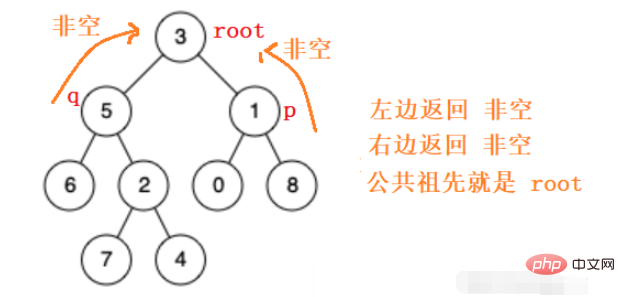
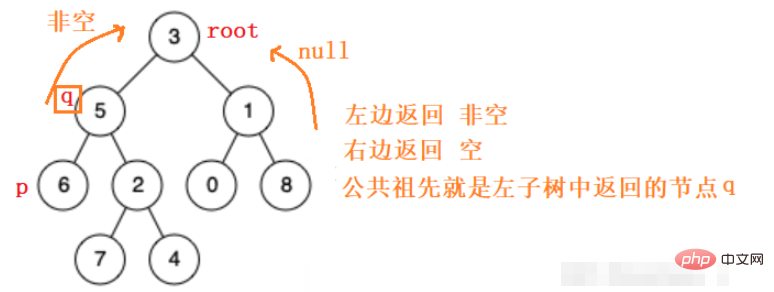
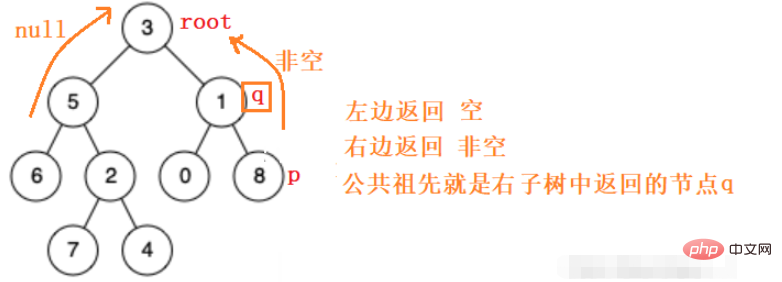
위의 아이디어에 따르면, 우리는 쉽게 코드를 작성할 수 있습니다

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if(root == null) return null;

    // p 为当前树的根节点
    if(p == root) return p;
    // q 为当前树的根节点
    if(q == root) return q;
    
    // 去左子树中找
    TreeNode left = lowestCommonAncestor(root.left,p,q);
    // 去右子树中找
    TreeNode right = lowestCommonAncestor(root.right,p,q);

    // 左边右边都找到了
    if(left != null && right != null) {
        return root;
    }
    // 左边找到了，右边没找到
    if(left != null) {
        return left;
    }
    if(right != null) {
        return right;
    }
    return null;
}

아이디어 2: 트리가 자식 부모 표현으로 표현된다고 가정

각 노드는 아버지의 주소를 저장합니다 노드를 사용하면 공통 조상인 두 연결 목록의 첫 번째 교차점을 찾을 때까지 레이어별로 온라인 레이어를 검색할 수 있습니다.

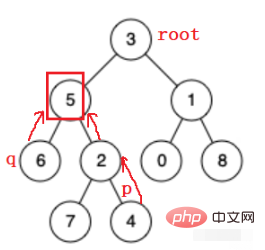
일반 이진 트리의 경우 위쪽이 아닌 레이어별로 아래쪽으로만 검색할 수 있으므로 두 경로 중 마지막 동일한 노드까지 두 노드의 경로를 유지해야 합니다. 여기서는 스택을 사용하여 두 노드의 경로를 유지합니다.

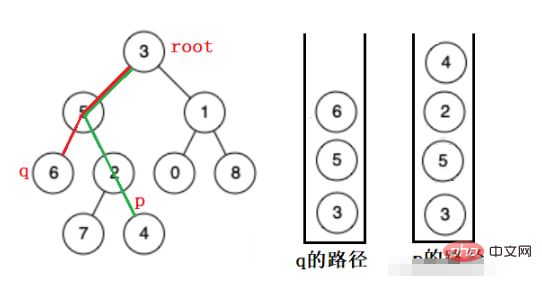
먼저 더 많은 요소가 포함된 스택의 요소를 팝한 다음, 팝할 노드가 같아질 때까지 두 스택을 함께 팝합니다. 이는 가장 가까운 공통 조상입니다.

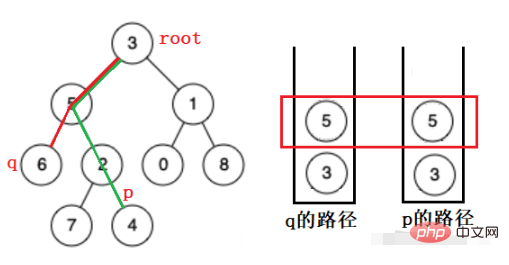
그럼 여기서 가장 큰 어려움은 보관 경로입니다.

여기서 스택은 경로를 저장하는 데 사용됩니다. 노드를 순회하면 노드가 스택에 들어간 다음 노드의 왼쪽 및 오른쪽 트리를 재귀적으로 검색하여 경로를 찾습니다. 유지되며, 발견되지 않으면 팝됩니다.

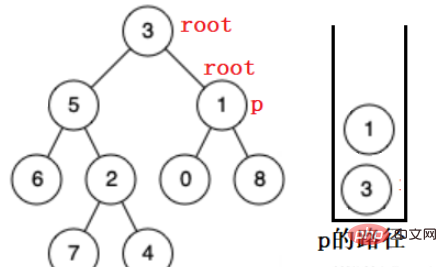
아래 그림에서 p를 찾고 있다고 가정해 보겠습니다.

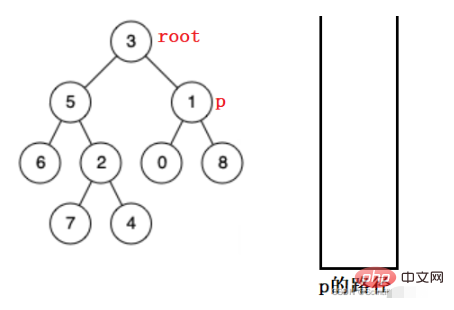
먼저 루트 노드를 스택에 넣고, 루트 노드의 왼쪽 하위 트리에서 재귀적으로 검색하고, 찾을 수 없으면 팝업하여 오른쪽에서 검색합니다. 하위 트리.

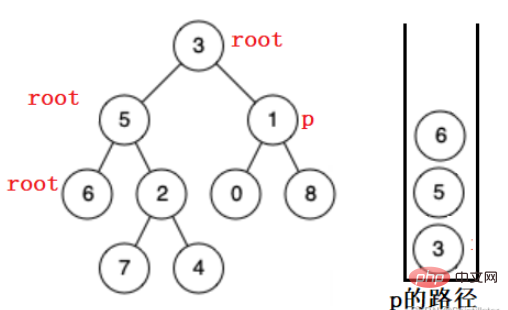
루트가 6에 도달하면 노드의 왼쪽과 오른쪽이 비어 있는 것을 발견합니다. 이는 하위 트리에서 대상 노드를 찾을 수 없음을 나타냅니다. 6이 팝업되어 5의 오른쪽 하위 트리에서 계속 검색됩니다. .

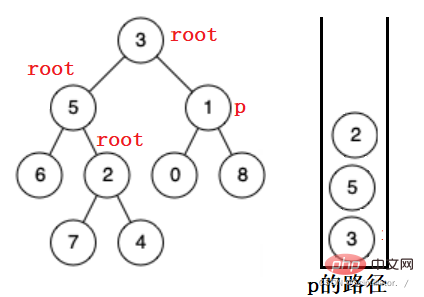
마찬가지로 5의 오른쪽 하위 트리에서는 찾을 수 없습니다. 1을 찾기 위해 3의 오른쪽 하위 트리로 갈 때까지 팝업됩니다. 발견됩니다.

rreee

위 내용은 Java에서 이진 트리의 가장 가까운 공통 조상을 찾는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!