볼록 집합 투영(POCS)을 기반으로 하는 클러스터링 알고리즘

POCS: 볼록 세트에 대한 투영. 수학에서 볼록 집합은 두 점 사이의 선분이 집합 내에 있는 집합입니다. 투영은 한 점을 다른 공간의 하위 공간에 매핑하는 작업입니다. 볼록 집합과 점이 주어지면 점의 볼록 집합에 대한 투영을 찾아 연산할 수 있습니다. 투영은 점에 가장 가까운 볼록 집합의 점이며 이 점과 볼록 집합의 다른 점 사이의 거리를 최소화하여 계산할 수 있습니다. 투영이기 때문에 특징을 다른 공간의 볼록한 집합에 매핑할 수 있으므로 클러스터링이나 차원 축소와 같은 작업을 수행할 수 있습니다.

이 글에서는 볼록 집합 투영법 기반의 클러스터링 알고리즘, 즉 POCS 기반의 클러스터링 알고리즘을 검토합니다. 원본 논문은 IWIS2022에 게재되었습니다.

볼록 집합

볼록 집합은 데이터 점 집합으로 정의되며, 집합의 두 점 x1과 x2를 연결하는 선분은 이 집합에 완전히 포함됩니다. 볼록 집합의 정의에 따르면 빈 집합 ∅, 단일 집합, 선분, 초평면 및 유클리드 구는 모두 볼록 집합으로 간주됩니다. 데이터 포인트는 싱글톤 세트(단 하나의 요소만 포함하는 세트)이기 때문에 볼록 세트로 간주됩니다. 이는 클러스터링된 데이터 포인트에 POCS 개념을 적용하기 위한 새로운 경로를 열어줍니다.

POCS(볼록 집합 투영)

POCS 방법은 대략 교대형과 병렬형의 두 가지 유형으로 나눌 수 있습니다.

1. 교대 POC

데이터 공간의 임의 지점에서 시작하면 이 지점에서 두 개(또는 그 이상)의 교차하는 볼록 집합으로의 교대 투영은 다음 그림과 같이 집합 교점 내의 한 지점으로 수렴됩니다.

볼록 집합이 분리되면 교대 투영은 투영 순서에 따라 달라지는 욕심 많은 극한 주기로 수렴됩니다.

2. 병렬 POCS

교대 형식과 달리 병렬 POCS 프로젝트는 데이터 포인트에서 모든 볼록 세트까지 동시에 진행되며 각 투영에는 중요도 가중치가 있습니다. 두 개의 비어 있지 않은 교차하는 볼록 세트의 경우 교대 버전과 유사하게 평행 투영은 세트의 교차점에 있는 점으로 수렴됩니다.

볼록 집합이 교차하지 않는 경우 투영은 최소 솔루션으로 수렴됩니다. POC 기반 클러스터링 알고리즘의 주요 아이디어는 이 기능에서 비롯됩니다.

POCS에 대한 자세한 내용은 원본 논문을 참조하세요.

POC 기반 클러스터링 알고리즘

논문 작성자는 병렬 POCS 방법의 융합을 활용하여 매우 간단하지만 효과적인 클러스터링 알고리즘을 제안했습니다. 어느 정도 클래스 알고리즘. 알고리즘은 기존 K-Means 알고리즘과 유사하게 작동하지만 각 데이터 포인트가 처리되는 방식에 차이가 있습니다. K-Means 알고리즘은 각 데이터 포인트의 중요도에 동일한 가중치를 부여하지만 POC 기반 클러스터링 알고리즘은 각 데이터 포인트 중요도에 따라 다르게 가중치가 부여되며 이는 클러스터 프로토타입에서 데이터 포인트까지의 거리에 비례합니다.

알고리즘의 의사 코드는 다음과 같습니다.

실험 결과

저자는 일부 공개 벤치마크 데이터 세트에서 POC 기반 클러스터링 알고리즘의 성능을 테스트했습니다. 아래 표에는 이러한 데이터 세트에 대한 설명이 요약되어 있습니다.

저자는 POC 기반 클러스터링 알고리즘의 성능을 k-평균 및 퍼지 C-평균 알고리즘을 포함한 다른 기존 클러스터링 방법과 비교했습니다. 다음 표에는 실행 시간 및 클러스터링 오류 측면에서 평가가 요약되어 있습니다.

클러스터링 결과는 다음과 같습니다.

예제 코드

우리는 매우 간단한 데이터 세트에 이 알고리즘을 사용합니다. 저자는 애플리케이션에 직접 사용할 수 있는 직접 사용 패키지를 출시했습니다.

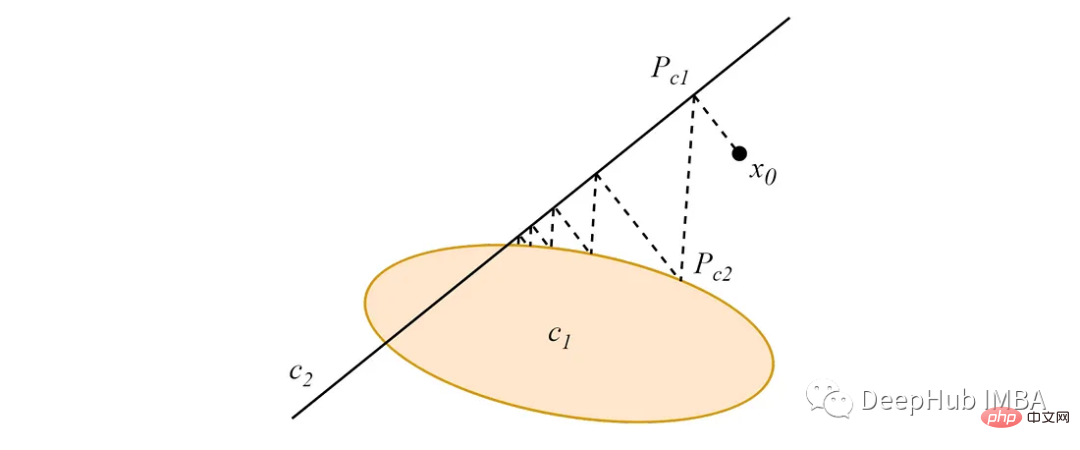
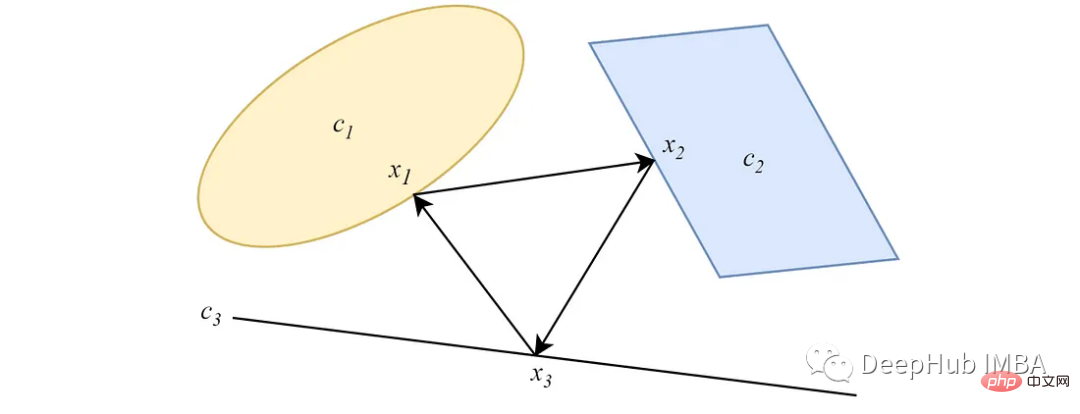
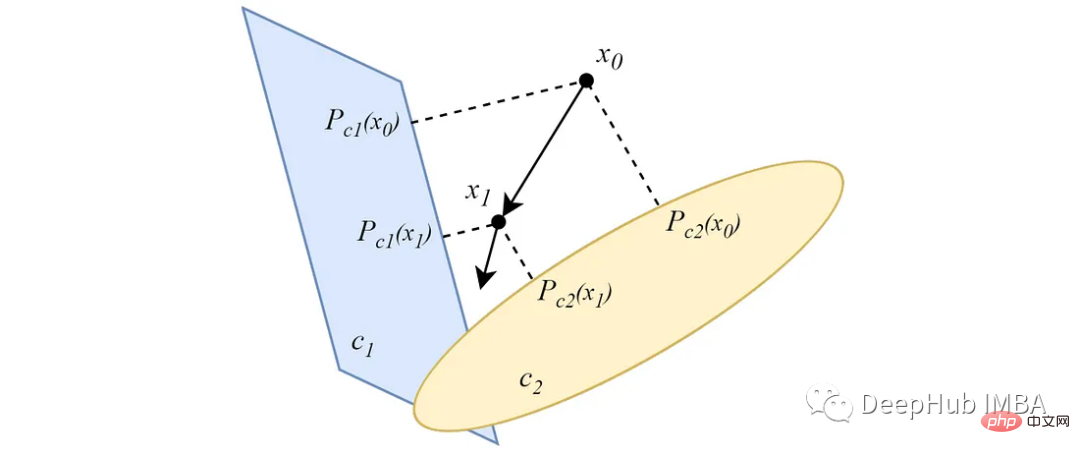
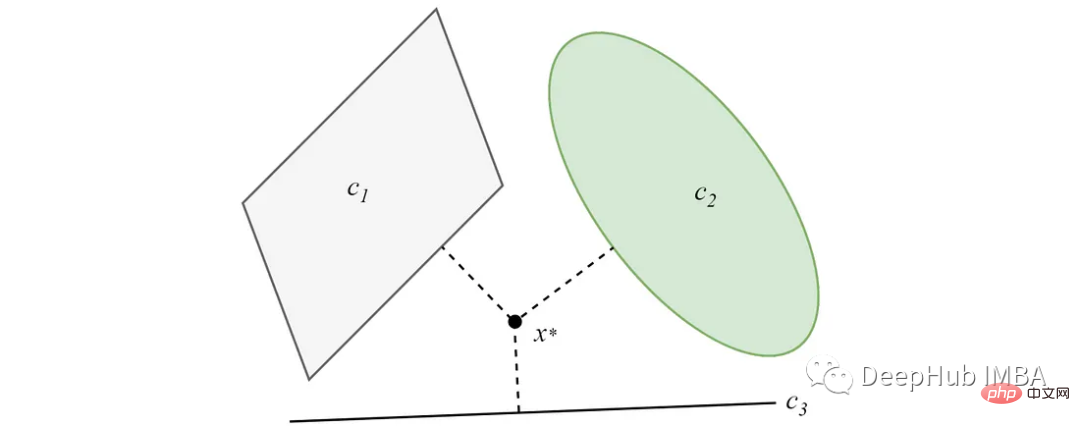
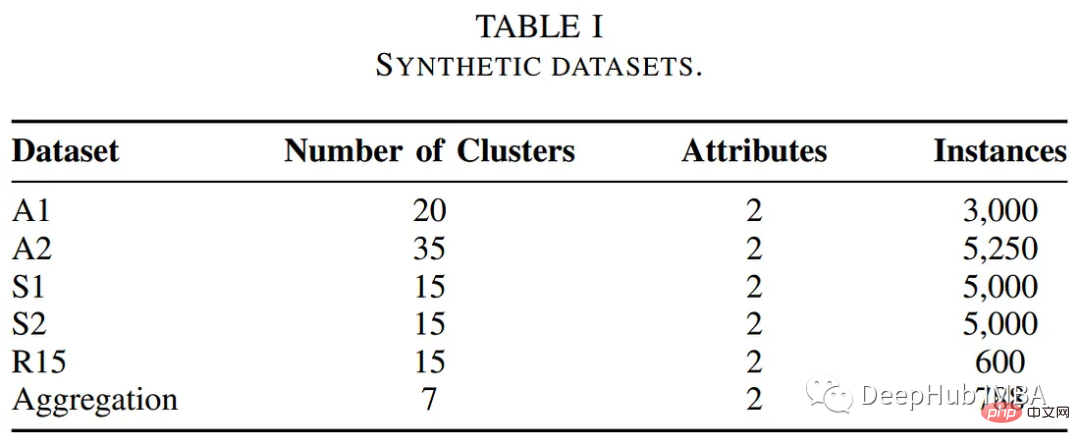
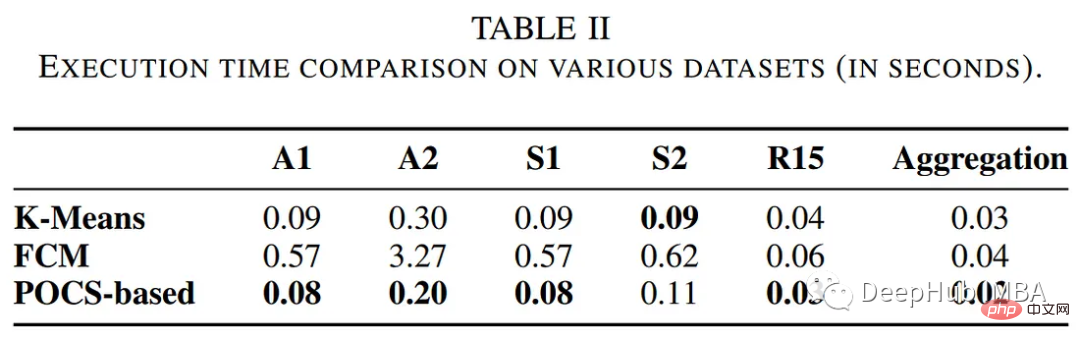
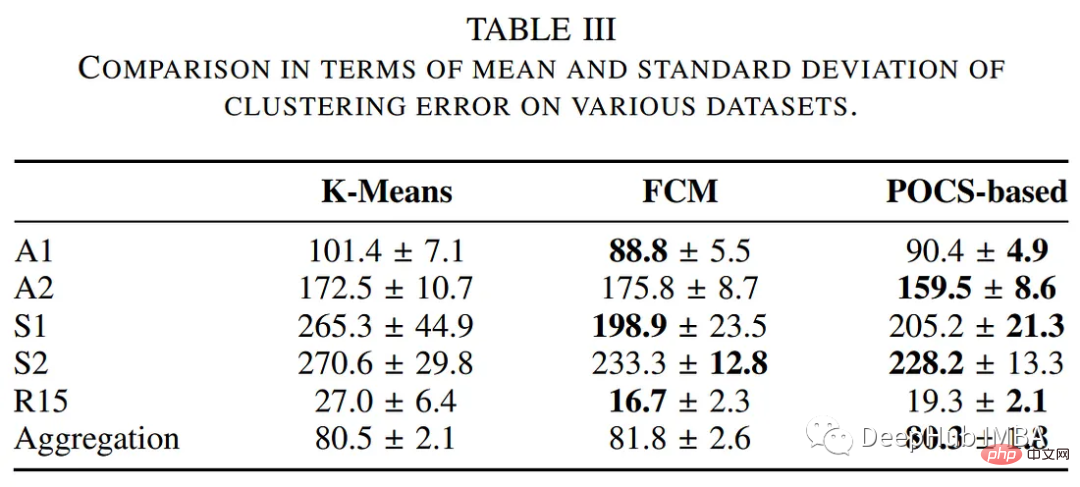
pip install pocs-based-clustering

10개의 클러스터를 중심으로 5000개의 데이터 포인트로 구성된 간단한 데이터 세트 만들기:

# Import packages
 import time
 import matplotlib.pyplot as plt
 
 from sklearn.datasets import make_blobs
 from pocs_based_clustering.tools import clustering
 
 
 # Generate a simple dataset
 num_clusters = 10
 X, y = make_blobs(n_samples=5000, centers=num_clusters, 
 cluster_std=0.5, random_state=0)
 
 plt.figure(figsize=(8,8))
 plt.scatter(X[:, 0], X[:, 1], s=50)
 plt.show()

클러스터링 수행 및 결과 표시:

# POSC-based Clustering Algorithm
 centroids, labels = clustering(X, num_clusters, 100)
 
 # Display results
 plt.figure(figsize=(8,8))
 plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
 plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red')
 plt.show()

总结

我们简要回顾了一种简单而有效的基于投影到凸集(POCS)方法的聚类技术，称为基于POCS的聚类算法。该算法利用POCS的收敛特性应用于聚类任务，并在一定程度上实现了可行的改进。在一些基准数据集上验证了该算法的有效性。

论文的地址如下：https://arxiv.org/abs/2208.08888

作者发布的源代码在这里：https://github.com/tranleanh/pocs-based-clustering

위 내용은 볼록 집합 투영(POCS)을 기반으로 하는 클러스터링 알고리즘의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!