Java에서 절반 삽입 정렬 알고리즘을 구현하는 방법

정렬 알고리즘 소개

정렬 알고리즘은 특정 알고리즘 요소를 통해 미리 결정된 패턴에 따라 하나 이상의 데이터 집합을 재정렬하는 것입니다. 최종 시퀀스는 특정 규칙에 따라 제시됩니다.

정렬 알고리즘에서 안정성과 효율성은 종종 고려해야 할 문제입니다.

안정성: 안정성은 두 개의 동일한 요소가 동시에 시퀀스에 나타날 때 특정 정렬 알고리즘 후에 정렬 전후의 두 요소의 상대적 위치가 변경되지 않음을 의미합니다.

복잡도 분석:

(1) 시간 복잡도: 정렬 알고리즘의 변환, 이동 등의 작업 후 시퀀스의 초기 상태에서 최종 정렬 결과 상태로 변경되는 데 걸리는 시간을 측정한 것입니다.

(2) 공간 복잡도: 시퀀스의 초기 상태부터 정렬 및 최종 상태로의 이동 변환 과정을 거쳐 소비되는 공간 오버헤드입니다.

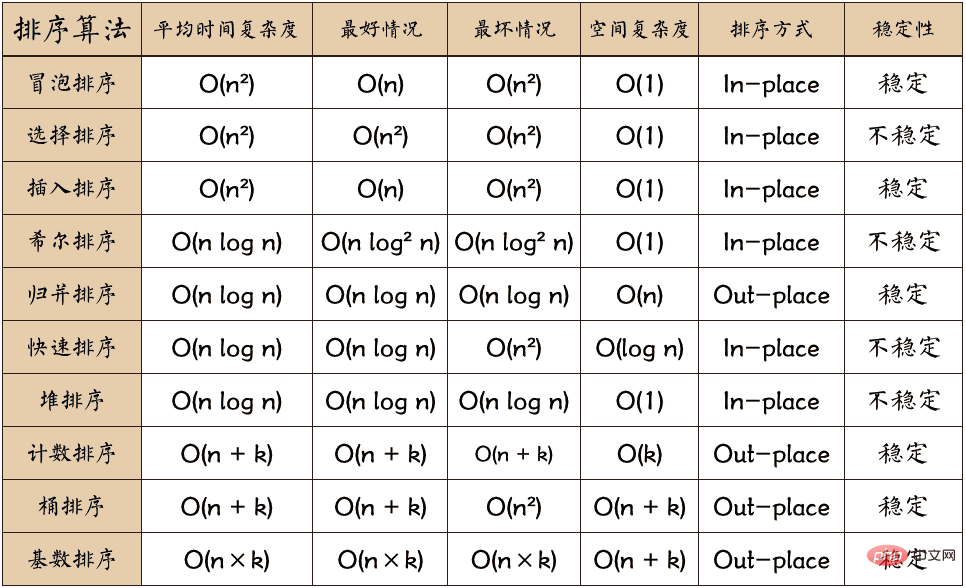
일반적인 정렬 알고리즘은 다음 유형으로 나뉩니다.

이진 삽입 정렬

원리

이진 삽입 정렬은 삽입 정렬 알고리즘을 개선한 것입니다. 이전에 정렬된 시퀀스에 요소를 지속적으로 삽입합니다. 전반부는 정렬된 순서이므로 삽입점을 순서대로 검색할 필요가 없으며 삽입점 검색 속도를 높이기 위해 절반 검색 방법을 사용할 수 있습니다.

코드 구현

정렬된 배열에 새 요소를 삽입하는 과정에서 삽입점을 찾을 때 삽입할 영역의 첫 번째 요소를 a[low]로 마지막 요소를 a[high]로 설정합니다. 그런 다음 각 비교 라운드에서 삽입할 요소는 a[m]과 비교됩니다. 여기서 m = (low+high)/2가 참조 요소보다 작으면 a[low]가 a[입니다. m-1]이 새 영역으로 선택됩니다(예: high=m-1). 그렇지 않으면 a[m+1] ~ a[high]를 새 삽입 영역(예: low=m+1)으로 선택합니다. , low

즉, 정렬된 요소를 활용하고 반 검색 기능을 사용하면 삽입할 위치를 빠르게 찾을 수 있습니다.

    // Binary Insertion Sort method    
    private static void binaryInsertSort(int[] array){
       
        for(int i = 1; i < array.length; i++){
           
            int temp = array[i];            
            int low = 0;            
            int high = i - 1;  
           
            while(low <= high){                
                int mid = (low + high) / 2;                
                if(temp < array[mid]){                    
                    high = mid - 1;                
                }else{                    
                    low = mid + 1;
                }       
            }
           
            for(int j = i; j >= low + 1; j--){            
                array[j] = array[j - 1];                                                      
            }       
           
            array[low] = temp;       
        }   
    }

복잡도 분석

반삽입 정렬 알고리즘은 직접 삽입 알고리즘에 비해 키워드 간 비교 횟수가 현저히 줄어들어 직접 삽입 정렬 알고리즘보다 빠르지만 레코드 이동 횟수가 늘어납니다. 변경되지 않으므로 절반 삽입 정렬 알고리즘의 시간 복잡도는 여전히 O(n^2)이며 이는 직접 삽입 정렬 알고리즘과 동일합니다.

시간 복잡도

최고의 경우: O(n). 요소를 정방향으로 정렬하면 검색이나 이동 없이 처음부터 바로 위치를 찾을 수 있습니다.

최악의 경우: O(n^2). 요소를 역순으로 정렬하면 매번 데이터 조회가 필요합니다.

평균 복잡성: O(n^2).

공간 복잡도: O(1). 핵심 정보 단위를 기록하는 데는 몇 개의 저장 공간만 필요합니다. 즉, 공간 복잡도는 O(1)입니다.

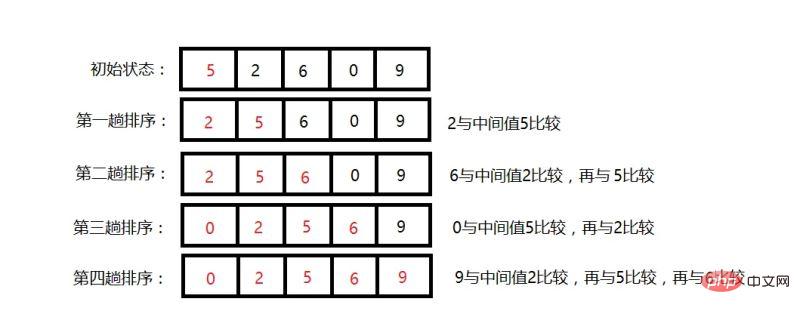
예:

알고리즘 연습

알고리즘의 전반적인 아이디어는 위에 설명되어 있습니다. 예를 사용하여 물을 직접 테스트해 보겠습니다.

반삽입 정렬

문제 설명:

정수 배열 num을 주었습니다. 배열을 오름차순으로 정렬해 주세요.

예 1:

입력: nums = [5,2,3,1]

출력: [1,2,3,5]

예 2:

입력: nums = [5,1,1 ,2,0,0]

출력: [0,0,1,1,2,5]

힌트:

1

-5 * 104 < ;= 숫자[i]

class Solution {
    public int[] sortArray(int[] nums) {
        for(int i = 1; i < nums.length; i++){
           
            int temp = nums[i];            
            int low = 0;            
            int high = i - 1;  
           
            while(low <= high){                
                int mid = (low + high) / 2;                
                if(temp < nums[mid]){                    
                    high = mid - 1;                
                }else{                    
                    low = mid + 1;
                }       
            }
           
            for(int j = i; j >= low + 1; j--){            
                nums[j] = nums[j - 1];                                                      
            }       
           
            nums[low] = temp;       
        }   
        return nums;
    }
}

위 내용은 Java에서 절반 삽입 정렬 알고리즘을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!