Java에서 최소 스패닝 트리를 찾는 방법
- WBOY앞으로
- 2023-04-29 18:58:13750검색
1 최소 스패닝 트리 개요
스패닝 트리: 연결된 그래프의 스패닝 트리는 그래프의 모든 n 꼭지점을 포함하지만 트리를 형성하기에 충분한 n개만 포함하는 연결된 하위 그래프를 나타냅니다. . n개의 정점이 있는 스패닝 트리에는 n-1개의 가장자리만 있습니다. 스패닝 트리에 다른 가장자리가 추가되면 확실히 순환이 형성됩니다.
최소 스패닝 트리: 연결된 그래프의 모든 스패닝 트리 중 모든 간선과 가장 작은 스패닝 트리의 가중치를 최소 스패닝 트리라고 합니다.
생활에서 그래픽 구조가 가장 널리 사용됩니다. 예를 들어, 공통 통신망 구축 경로 선택에서 마을은 정점으로 간주될 수 있으며, 마을 간에 통신 경로가 있는 경우 두 지점 사이의 가장자리 또는 호로 계산될 수 있습니다. 가장자리 또는 호 가중치 값.
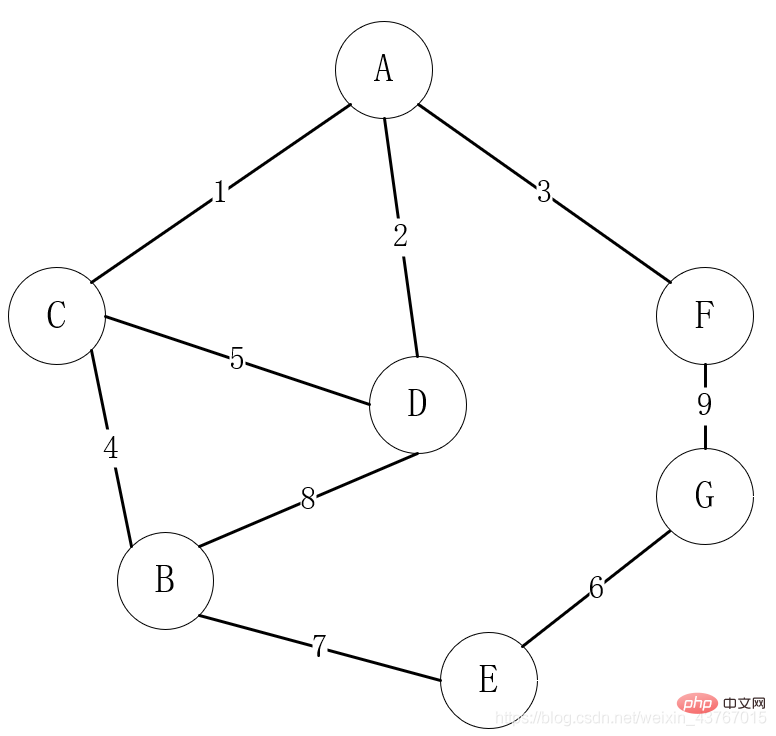
위 그림은 생활 속 통신망 구축 경로의 선택을 그래프 구조로 매핑한 사례입니다. 정점은 마을 역할을 하며, 마을 간에 통신 경로가 있으면 가장자리가 있습니다. 마을 간 통신을 설정하는 데 드는 비용은 가장자리의 무게입니다.
매우 일반적인 요구 사항은 의사소통이 가능한 모든 마을이 의사소통을 해야 한다는 것이고, 통신 구축 비용은 결국 자금이 "한정"되어 자금이 절약된다는 것입니다.
위 문제를 수학적 모델로 변환하면 그래프의 최소 스패닝 트리를 찾는 문제, 즉 연결된 모든 정점을 연결하고 가중치의 합이 가장 작은 경로를 선택하는 문제입니다. 이 문제에 대한 많은 해결책이 있습니다. 가장 고전적인 두 가지 알고리즘은 Prim의 알고리즘과 Kruskal의 알고리즘입니다.
2 프림의 알고리즘(Prim)
2.1 원리
프림의 알고리즘은 모든 꼭지점이 연결되어 있지 않다고 가정하고 특정 꼭지점에서 시작하여 점차적으로 각 꼭지점에서 가장 작은 가중치를 갖는 모서리를 찾아 결합을 연결하는 최소값을 구성합니다. 스패닝 트리. 최소 스패닝 트리를 구축하기 위해 포인트를 목표로 사용합니다.
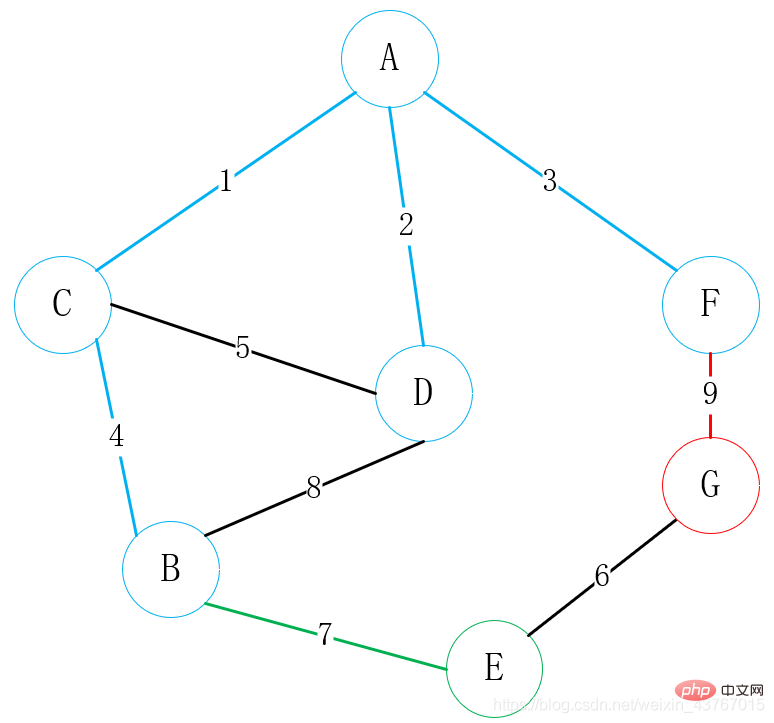
구체적인 단계는 다음과 같습니다. 먼저 정점 a를 무작위로 선택하고 정점 a가 연결할 수 있는 모든 정점을 찾은 다음 연결할 가중치가 낮은 정점을 선택한 다음 이 두 정점에 연결할 수 있는 모든 정점을 찾고 가중치를 선택합니다. 낮은 값을 가진 정점은 정점 중 하나에 연결됩니다. 이는 n-1 번 앞뒤로 이동하며, 매번 연결된 끝 정점에 가장 짧은 정점을 선택하여(첫 번째 정점에 가장 짧은 정점이 아닌) 모든 정점에 연결됩니다. 정점을 연결하여 최소 스패닝 트리를 구성합니다.
2.2 사례 분석
이 사례는 아래 구현 코드의 사례에 해당합니다.
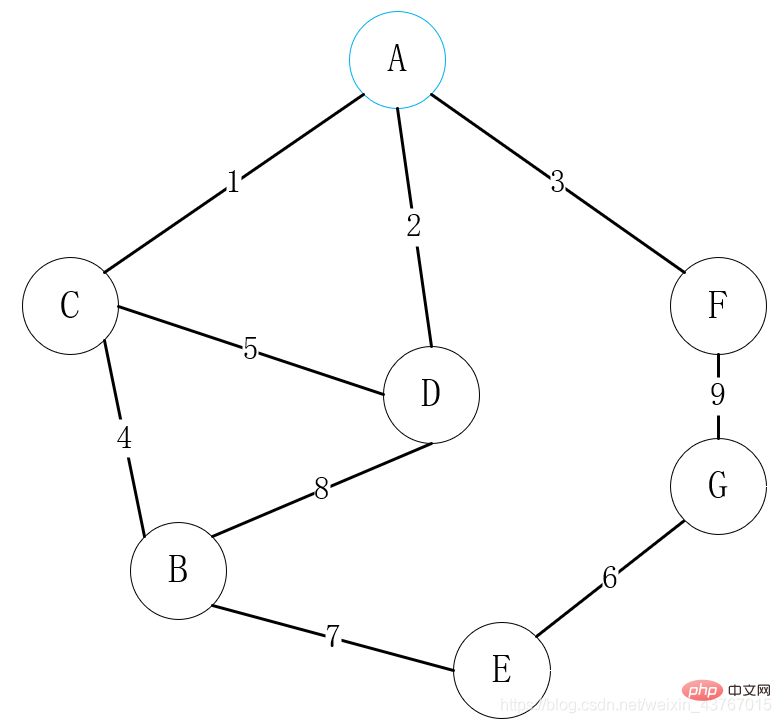
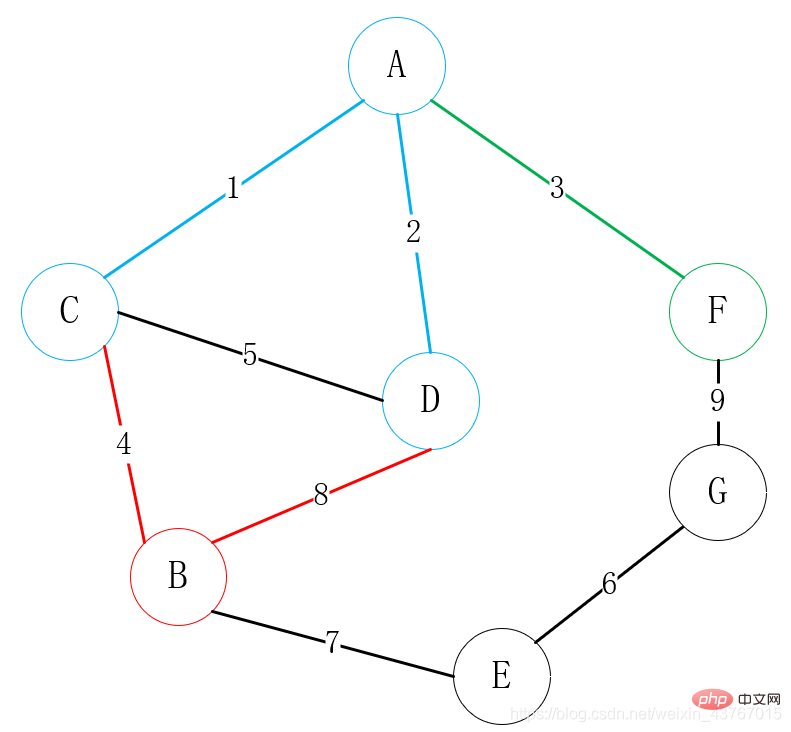
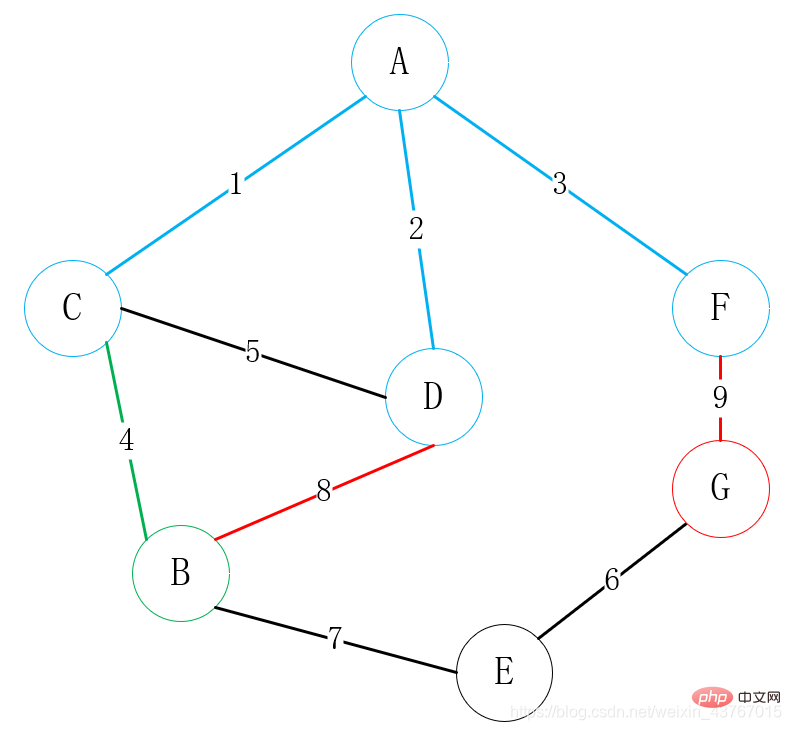
위 그림에서 먼저 정점 A를 연결점으로 선택하고 모든 정점 C, D, F를 연결할 수 있는 정점 A를 찾은 다음 연결할 가중치가 낮은 정점을 선택합니다. 여기서는 A-C를 선택합니다.
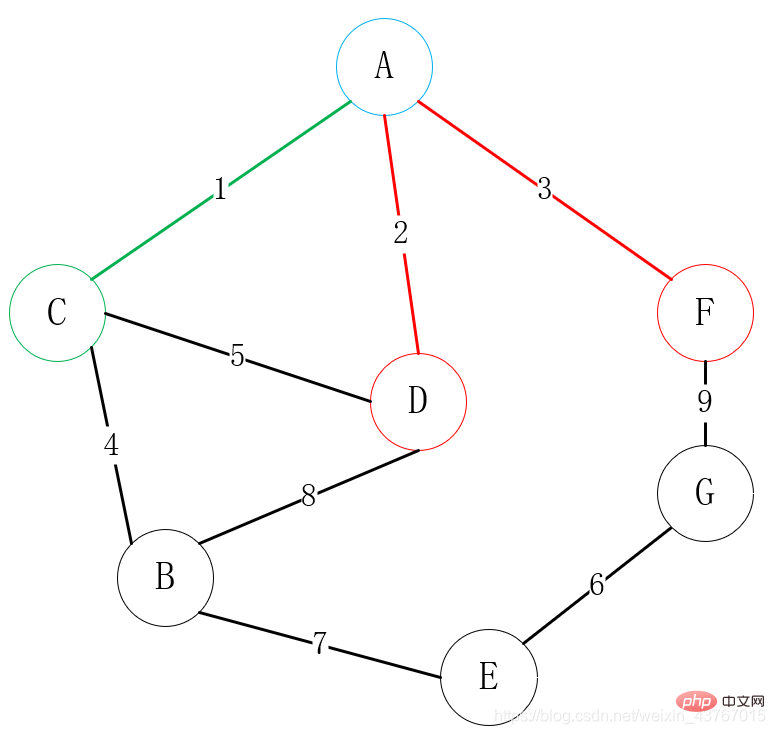
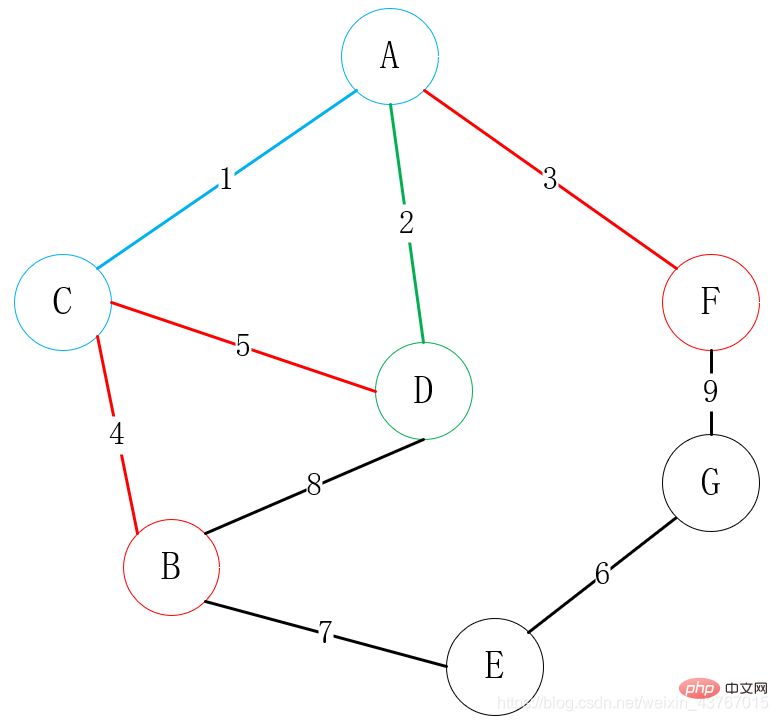
3 크루스칼 알고리즘(Kruskal)
3.1 원리
크루스칼 알고리즘(Kruskal)은 간선 가중치를 기준으로 점차적으로 최소 신장 트리를 구축하고, 간선을 목표로 하여 최소 신장 트리를 구축합니다.
구체적인 단계는 다음과 같습니다. 가중치 그래프의 각 꼭지점을 숲으로 처리한 다음 그래프에서 인접한 각 가장자리의 가중치를 오름차순으로 정렬한 다음 배열된 인접한 가장자리 테이블에서 가장 작은 가중치를 추출합니다. 가장자리에 대해 다음과 같이 작성합니다. Edge의 시작 정점과 끝 정점을 연결하여 숲을 형성한 후, 시작 정점과 끝 정점의 인접한 Edge를 읽고, 작은 가중치로 인접한 Edge에 우선 순위를 부여한 후 계속해서 정점을 연결하여 트리를 형성합니다. 숲을 나무로. 인접 간선을 추가하기 위한 요구 사항은 그래프에 추가된 인접 간선이 순환(링)을 형성하지 않는다는 것입니다. 이는 n-1개의 모서리가 추가될 때까지 반복됩니다. 이 시점에서 최소 스패닝 트리가 구성됩니다.
3.2 사례 분석
이 사례는 아래 구현 코드의 사례에 해당합니다. 전통적인 Kruskal 알고리즘 프로세스는 다음과 같습니다.
먼저 Edge Set 배열을 가져와서 사용하는 가중치에 따라 정렬합니다. 정렬 정렬을 코드에서 직접 수행할 수도 있으며 정렬 후 결과는 다음과 같습니다.
Edge{from=A, to=C, Weight=1}
Edge{from=D , to=A, 가중치=2}
Edge {from=A, to=F, Weight=3}
Edge{from=B, to=C, Weight=4}
Edge{from=C, to=D, 무게=5}
가장자리{from=E, to=G, 무게=6}
가장자리{from=E, to=B, 무게=7}
가장자리{from=D, to=B, 무게=8}
Edge{from=F, to=G, Weight =9}
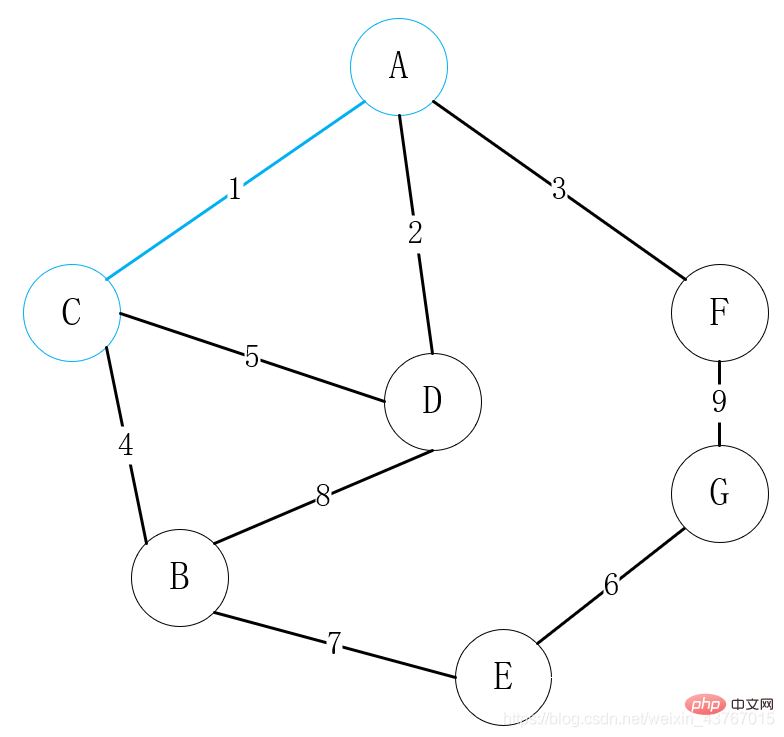
첫 번째 Edge A-C를 반복하고, 발견된 최소 스패닝 트리로 순환을 형성하지 않을 것이라고 판단하고, 총 가중치를 1만큼 늘리고, 계속합니다.
두 번째 가장자리 D-A를 루프 아웃하고, 발견된 최소 스패닝 트리는 사이클을 형성하지 않으며 가중치의 합은 2만큼 증가합니다. 계속
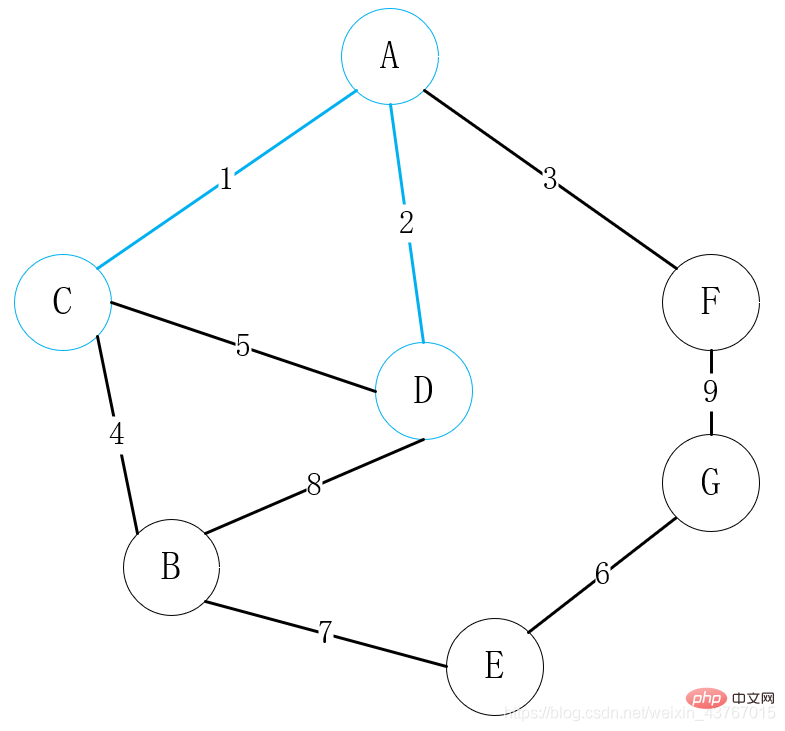세 번째 가장자리 A-F를 루프합니다. 그리고 발견된 최소 스패닝 트리는 사이클을 형성하지 않을 것으로 판단되며, 가중치의 합은 3만큼 증가합니다. 계속해서 4번째 모서리 B-C를 루프 아웃하고, a를 형성하지 않을 것으로 판단합니다. 발견된 최소 스패닝 트리로 순환하면 총 가중치가 4만큼 증가하고 계속
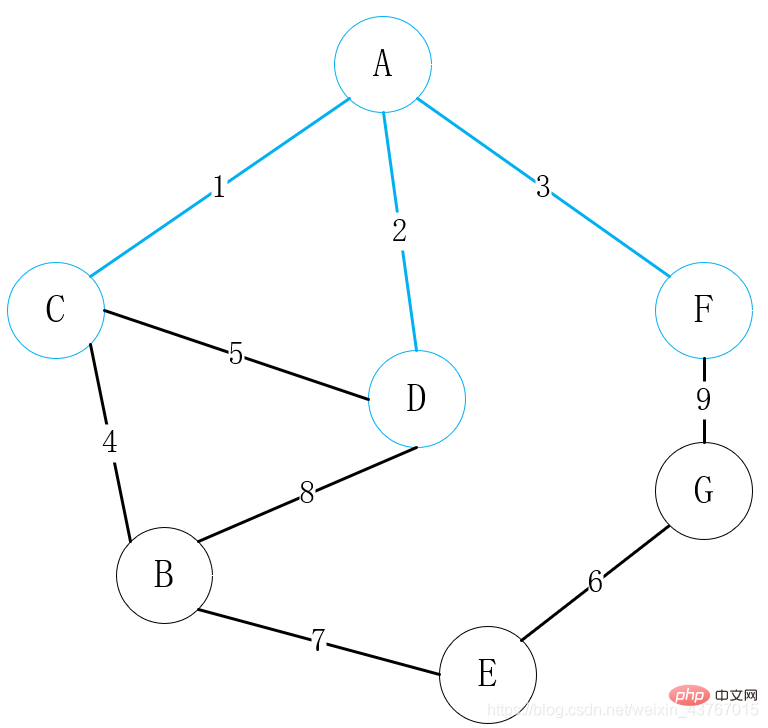5번째 모서리 C-D를 루프아웃하고, 발견된 최소 스패닝 트리로 순환을 형성할 것으로 판단됩니다. , 이 에지를 버리고 계속합니다.
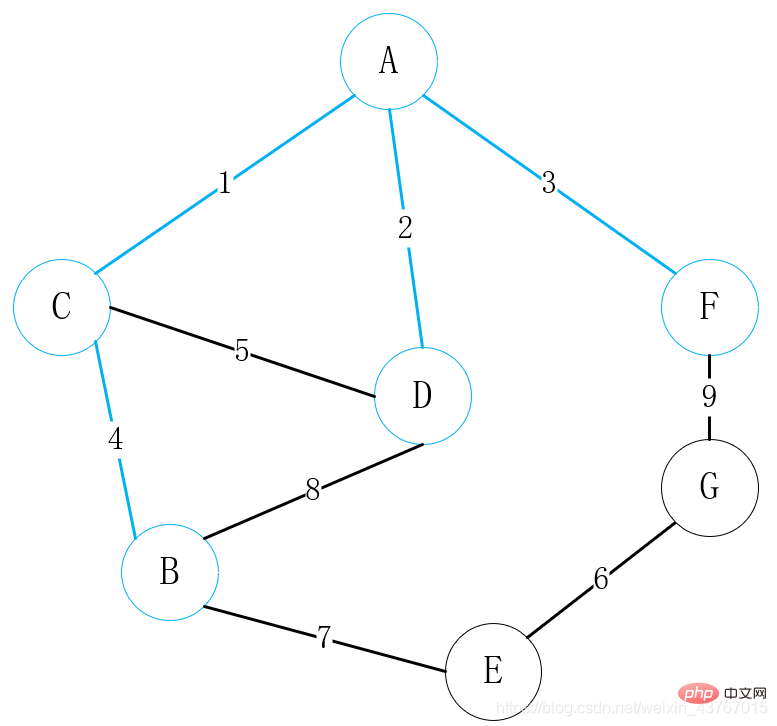6번째 에지 E-G를 루프 아웃합니다. 발견된 최소 스패닝 트리로 사이클을 형성하지 않을 것으로 판단되어 총 가중치가 6만큼 증가합니다. 계속;
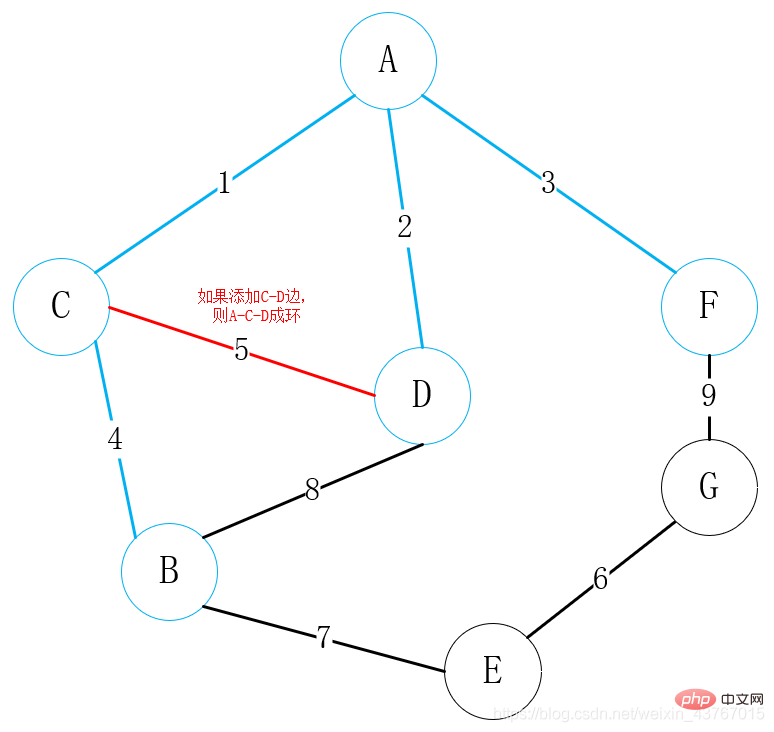7번째 모서리 E-B를 루프 아웃하고, 발견된 최소 스패닝 트리로 사이클을 형성하지 않을 것으로 판단하고, 총 가중치가 7만큼 증가하고, 계속
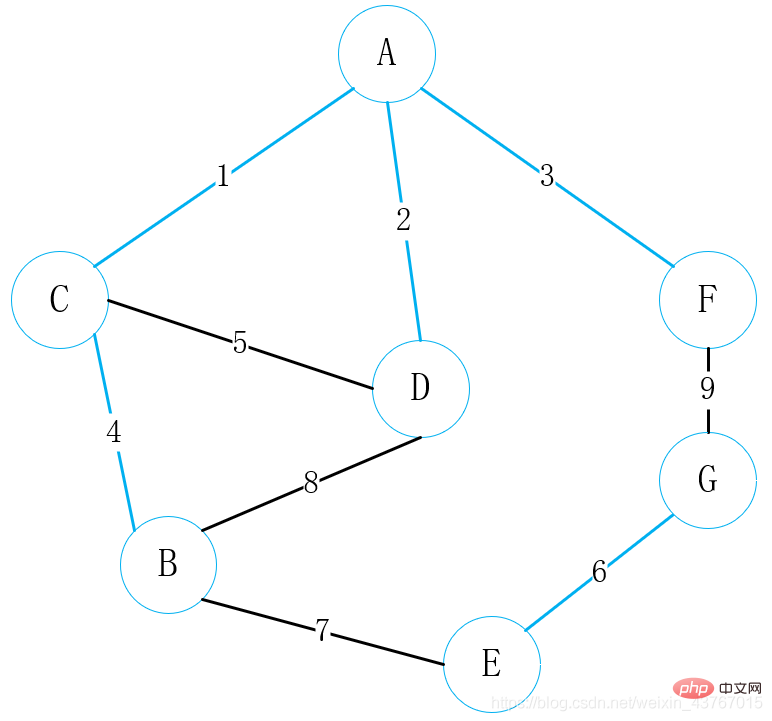8번째 모서리 D-B를 루프 아웃합니다. 발견된 최소 스패닝 트리로 사이클을 형성할 것으로 판단하고, 이 에지를 버리고 계속
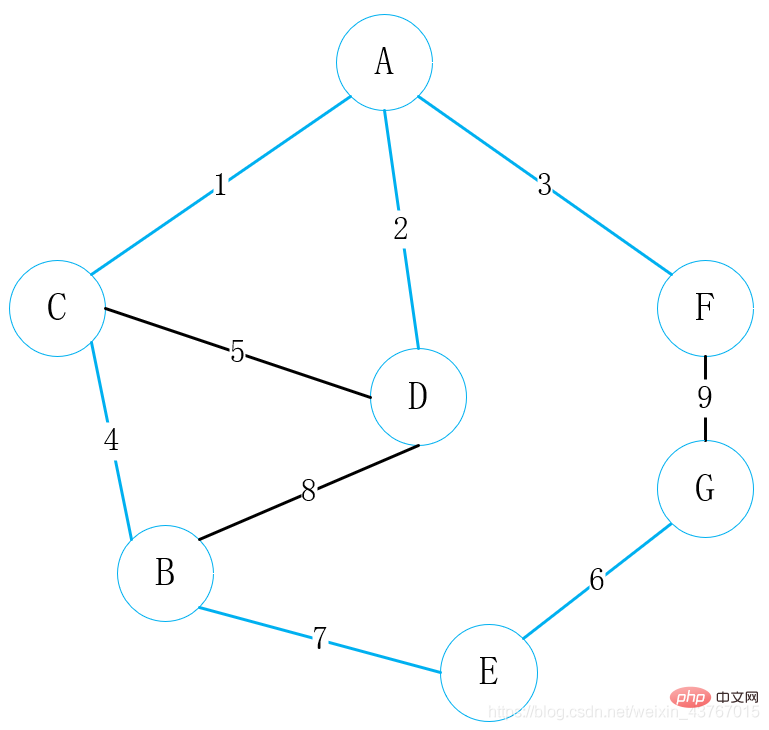9번째 에지 F-G를 루프 아웃하면 최소 스패닝 트리로 사이클을 형성할 것으로 판단됩니다. ;
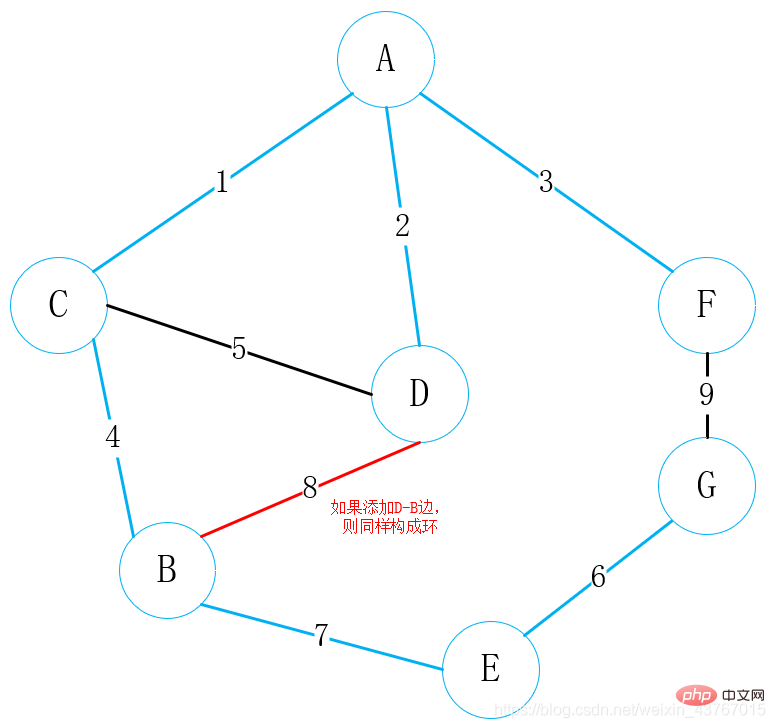이 시점에서 루프가 끝나면 최소 스패닝 트리가 발견되었으며 최소 스패닝 트리의 총 가중치는 23입니다.
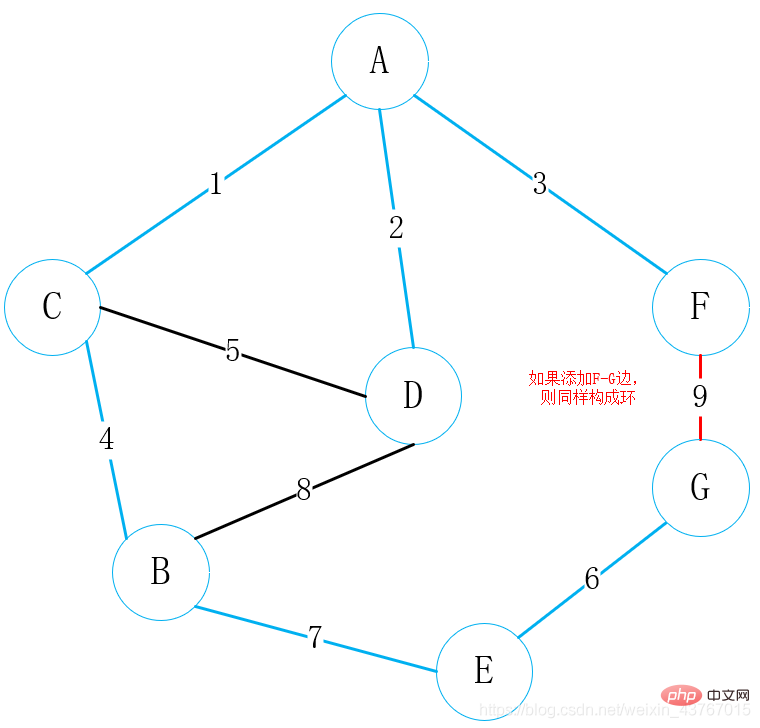위 단계에서 순환이 형성되었는지 확인하는 것이 중요합니다. 일반적인 접근 방식은 발견된 최소 스패닝 트리의 꼭지점을 시작점에서 끝점까지 정렬하는 것입니다. 그런 다음 새 가장자리가 추가될 때마다 새로 추가된 가장자리를 사용합니다. 가장자리의 시작점과 끝점은 최소 이진 트리에서 검색됩니다. 정렬된 끝점이 동일하면 최소 스패닝 트리에 이 가장자리를 더한 것을 의미합니다. 그렇지 않으면 그렇지 않음을 의미하며 정렬된 끝점이 업데이트됩니다.
4 인접 행렬 가중 그래프 구현
여기서의 구현은 인접 행렬을 기반으로 무방향 가중 그래프를 구현하는 클래스를 구성할 수 있으며, 깊이 우선 순회 및 너비 우선 순회를 위한 방법을 제공하고, 가장자리 집합 배열을 얻는 방법을 제공합니다. , 최소 스패닝 트리를 찾는 Prim과 Kruskal의 두 가지 방법을 제공합니다.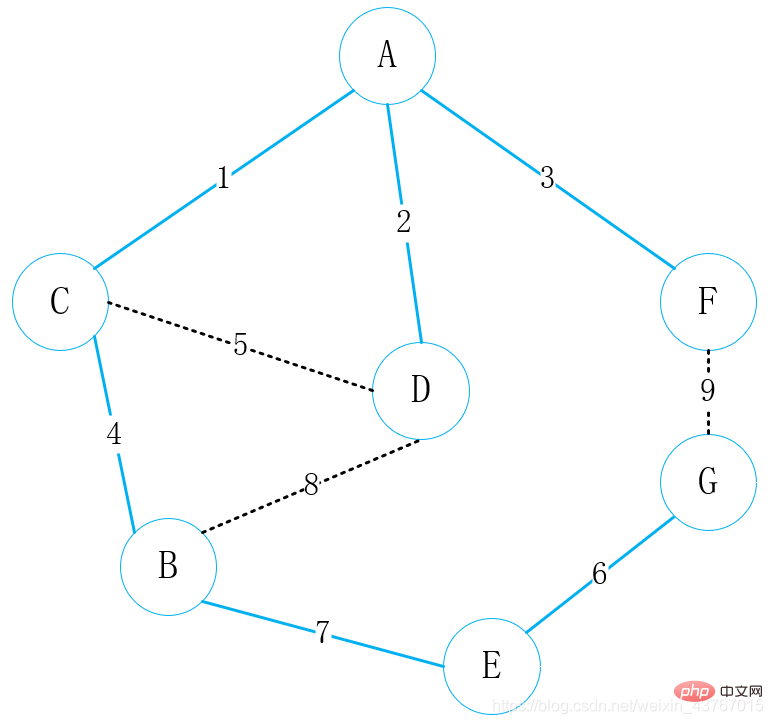 
/**
* 无向加权图邻接矩阵实现
* {@link MatrixPrimAndKruskal#MatrixPrimAndKruskal(E[], Edge[])} 构建无向加权图
* {@link MatrixPrimAndKruskal#DFS()} 深度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#BFS()} 广度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#toString()} 输出无向加权图
* {@link MatrixPrimAndKruskal#prim()} Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskal()} Kruskal算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskalAndPrim()} Kruskal算法结合Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#getEdges()} 获取边集数组
*
* @author lx
* @date 2020/5/14 18:13
*/
public class MatrixPrimAndKruskal<E> {
/**
* 顶点数组
*/
private Object[] vertexs;
/**
* 邻接矩阵
*/
private int[][] matrix;
/**
*
*/
private Edge<E>[] edges;
/**
* 由于是加权图,这里设置一个边的权值上限,任何边的最大权值不能大于等于该值，在实际应用中，该值应该根据实际情况确定
*/
private static final int NO_EDGE = 99;
/**
* 边对象,具有权值,在构建加权无向图时使用
*/
private static class Edge<E> {
private E from;
private E to;
private int weight;
public Edge(E from, E to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
/**
* 创建无向加权图
*
* @param vertexs 顶点数组
* @param edges 边对象数组
*/
public MatrixPrimAndKruskal(Object[] vertexs, Edge<E>[] edges) {
//初始化边数组
this.edges = edges;
// 初始化顶点数组,并添加顶点
this.vertexs = Arrays.copyOf(vertexs, vertexs.length);
// 初始化边矩阵,并预先填充边信息
this.matrix = new int[vertexs.length][vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
if (i == j) {
this.matrix[i][j] = 0;
} else {
this.matrix[i][j] = NO_EDGE;
}
}
}
for (Edge<E> edge : edges) {
// 读取一条边的起始顶点和结束顶点索引值
int p1 = getPosition(edge.from);
int p2 = getPosition(edge.to);
//对称的两个点位都置为edge.weight,无向图可以看作相互可达的有向图
this.matrix[p1][p2] = edge.weight;
this.matrix[p2][p1] = edge.weight;
}
}
/**
* 获取某条边的某个顶点所在顶点数组的索引位置
*
* @param e 顶点的值
* @return 所在顶点数组的索引位置, 或者-1 - 表示不存在
*/
private int getPosition(E e) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == e) {
return i;
}
}
return -1;
}
/**
* 深度优先搜索遍历图,类似于树的前序遍历,
*/
public void DFS() {
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
//初始化所有顶点都没有被访问
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("DFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
DFS(i, visited);
}
}
System.out.println();
}
/**
* 深度优先搜索遍历图的递归实现,类似于树的先序遍历
* 因此模仿树的先序遍历,同样借用栈结构,这里使用的是方法的递归,隐式的借用栈
*
* @param i 顶点索引
* @param visited 访问标志数组
*/
private void DFS(int i, boolean[] visited) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
// 遍历该顶点的所有邻接点。若该邻接点是没有访问过，那么继续递归遍历领接点
for (int w = firstVertex(i); w >= 0; w = nextVertex(i, w)) {
if (!visited[w]) {
DFS(w, visited);
}
}
}
/**
* 广度优先搜索图,类似于树的层序遍历
* 因此模仿树的层序遍历,同样借用队列结构
*/
public void BFS() {
// 辅组队列
Queue<Integer> indexLinkedList = new LinkedList<>();
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("BFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
indexLinkedList.add(i);
}
if (!indexLinkedList.isEmpty()) {
//j索引出队列
Integer j = indexLinkedList.poll();
//继续访问j的邻接点
for (int k = firstVertex(j); k >= 0; k = nextVertex(j, k)) {
if (!visited[k]) {
visited[k] = true;
System.out.print(vertexs[k] + " ");
//继续入队列
indexLinkedList.add(k);
}
}
}
}
System.out.println();
}
/**
* 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*
* @param v 顶点v在数组中的索引
* @return 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*/
private int firstVertex(int v) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 从i=0开始*/
for (int i = 0; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*
* @param v 顶点索引
* @param w 第一个邻接点索引
* @return 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*/
private int nextVertex(int v, int w) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1) || w < 0 || w > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 由于邻接点w的索引已经获取了,所以从i=w+1开始寻找*/
for (int i = w + 1; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 输出图
*
* @return 输出图字符串
*/
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
stringBuilder.append(matrix[i][j]).append("\t");
}
stringBuilder.append("\n");
}
return stringBuilder.toString();
}
/**
* Prim算法求最小生成树
*/
public void prim() {
System.out.println("prim: ");
//对应节点应该被连接的前驱节点,用来输出
//默认为0,即前驱结点为第一个节点
int[] mid = new int[matrix.length];
//如果某顶点作为末端顶点被连接，对应位置应该为true
//第一个顶点默认被连接
boolean[] connected = new boolean[matrix.length];
connected[0] = true;
//存储未连接顶点到已连接顶点的最短距离(最小权)
int[] dis = new int[matrix.length];
//首先将矩阵第一行即其他顶点到0索引顶点的权值拷贝进去
System.arraycopy(matrix[0], 0, dis, 0, matrix.length);
//存储路径长度
int sum = 0;
//最小权值
int min;
/*默认第一个顶点已经找到了,因此最多还要需要大循环n-1次*/
for (int k = 1; k < matrix.length; k++) {
min = NO_EDGE;
//最小权值的顶点的索引
int minIndex = 0;
/*寻找权值最小的且未被连接的顶点索引*/
for (int i = 1; i < matrix.length; i++) {
//排除已连接的顶点,排除权值等于0的值,这里权值等于0表示已生成的最小生成树的顶点都未能与该顶点连接
if (!connected[i] && dis[i] != 0 && dis[i] < min) {
min = dis[i];
minIndex = i;
}
}
//如果没找到,那么该图可能不是连通图,直接返回了,此时最小生成树没啥意义
if (minIndex == 0) {
return;
}
//权值和增加
sum += min;
//该新连接顶点对应的索引值变成true,表示已被连接,后续判断时跳过该顶点
connected[minIndex] = true;
//输出对应的前驱顶点到该最小顶点的权值
System.out.println(vertexs[mid[minIndex]] + " ---> " + vertexs[minIndex] + " 权值:" + min);
/*在新顶点minIndex加入之前的其他所有顶点到连接顶点最小的权值已经计算过了
因此只需要更新其他未连接顶点到新连接顶点minIndex是否还有更短的权值,有的话就更新找到距离已连接的顶点权最小的顶点*/
for (int i = 1; i < matrix.length; i++) {
//如果该顶点未连接
if (!connected[i]) {
/*如果新顶点到未连接顶点i的权值不为0,并且比原始顶点到未连接顶点i的权值还要小,那么更新对应位置的最小权值*/
if (matrix[minIndex][i] != 0 && dis[i] > matrix[minIndex][i]) {
//更新最小权值
dis[i] = matrix[minIndex][i];
//更新前驱节点索引为新加入节点索引
mid[i] = minIndex;
}
}
}
}
System.out.println("sum: " + sum);
}
/**
* Kruskal算法求最小生成树传统实现,要求知道边集数组,和顶点数组
*/
public void kruskal() {
System.out.println("Kruskal: ");
//由于创建图的时候保存了边集数组,这里直接使用就行了
//Edge[] edges = getEdges();
//this.edges=edges;
//对边集数组进行排序
Arrays.sort(this.edges, Comparator.comparingInt(o -> o.weight));
// 用于保存已有最小生成树中每个顶点在该最小树中的最终终点的索引
int[] vends = new int[this.edges.length];
//能够知道终点索引范围是[0,this.edges.length-1],因此填充edges.length表示没有终点
Arrays.fill(vends, this.edges.length);
int sum = 0;
for (Edge<E> edge : this.edges) {
// 获取第i条边的起点索引from
int from = getPosition(edge.from);
// 获取第i条边的终点索引to
int to = getPosition(edge.to);
// 获取顶点from在"已有的最小生成树"中的终点
int m = getEndIndex(vends, from);
// 获取顶点to在"已有的最小生成树"中的终点
int n = getEndIndex(vends, to);
// 如果m!=n，意味着没有形成环路,则可以添加,否则直接跳过,进行下一条边的判断
if (m != n) {
//添加设置原始终点索引m在已有的最小生成树中的终点为n
vends[m] = n;
System.out.println(vertexs[from] + " ---> " + vertexs[to] + " 权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("sum: " + sum);
//System.out.println(Arrays.toString(this.edges));
}
/**
* 获取顶点索引i的终点如果没有终点则返回顶点索引本身
*
* @param vends 顶点在最小生成树中的终点
* @param i 顶点索引
* @return 顶点索引i的终点如果没有终点则返回顶点索引本身
*/
private int getEndIndex(int[] vends, int i) {
//这里使用循环查找的逻辑,寻找的是最终的终点
while (vends[i] != this.edges.length) {
i = vends[i];
}
return i;
}
/**
* 如果没有现成的边集数组，那么根据邻接矩阵结构获取图中的边集数组
*
* @return 图的边集数组
*/
private Edge[] getEdges() {
List<Edge> edges = new ArrayList<>();
/*遍历矩阵数组 只需要遍历一半就行了*/
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
//如果存在边
if (matrix[i][j] != NO_EDGE && matrix[i][j] != 0) {
edges.add(new Edge<>(vertexs[i], vertexs[j], matrix[i][j]));
//edges[index++] = new Edge(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges.toArray(new Edge[0]);
}
/**
* Kruskal结合Prim算法.不需要知道边集,只需要矩阵数组,和顶点数组
* 同样是求最小权值的边,但是有一个默认起点顶点,该起点可以是要求[0,顶点数量-1]之间的任意值，同时查找最小权的边。
* 可能会有Bug,目前未发现
*/
public void kruskalAndPrim() {
System.out.println("kruskalAndPrim: ");
//已经找到的边携带的顶点对应的索引将变为true,其余未找到边对应的顶点将是false
boolean[] connected = new boolean[matrix.length];
//这里选择第一个顶点为起点,表示以该顶点开始寻找包含该顶点的最小边
connected[0] = true;
int sum = 0, n1 = 0, n2 = 0;
//最小权值
int min;
while (true) {
min = NO_EDGE;
/*找出所有带有已找到顶点的边中,最小权值的边,只需要寻找对称矩阵的一半即可*/
//第一维
for (int i = 0; i < matrix.length; i++) {
//第二维
for (int j = i + 1; j < matrix.length; j++) {
//排除等于0的,排除两个顶点都找到了的,这里实际上已经隐含了排除环的逻辑,如果某条边的两个顶点都找到了,那么如果算上该条边,肯定会形成环
//寻找剩下的最小的权值的边
if (matrix[i][j] != 0 && connected[i] != connected[j] && matrix[i][j] < min) {
min = matrix[i][j];
n1 = i;
n2 = j;
}
}
}
//如果没找到最小权值,该图可能不是连通图,或者已经寻找完毕,直接返回
if (min == NO_EDGE) {
System.out.println(" sum:" + sum);
return;
}
//已经找到的边对应的两个顶点都置为true
connected[n1] = true;
connected[n2] = true;
//输出找到的边和最小权值
System.out.println(vertexs[n1] + " ---> " + vertexs[n2] + " 权值:" + min);
sum += min;
}
}
public static void main(String[] args) {
//顶点数组
Character[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//边数组,加权值
Edge[] edges = {
new Edge<>('A', 'C', 1),
new Edge<>('D', 'A', 2),
new Edge<>('A', 'F', 3),
new Edge<>('B', 'C', 4),
new Edge<>('C', 'D', 5),
new Edge<>('E', 'G', 6),
new Edge<>('E', 'B', 7),
new Edge<>('D', 'B', 8),
new Edge<>('F', 'G', 9)};
//构建图
MatrixPrimAndKruskal<Character> matrixPrimAndKruskal = new MatrixPrimAndKruskal<Character>(vexs, edges);
//输出图
System.out.println(matrixPrimAndKruskal);
//深度优先遍历
matrixPrimAndKruskal.DFS();
//广度优先遍历
matrixPrimAndKruskal.BFS();
//Prim算法输出最小生成树
matrixPrimAndKruskal.prim();
//Kruskal算法输出最小生成树
matrixPrimAndKruskal.kruskal();
//Kruskal算法结合Prim算法输出最小生成树,可能会有Bug,目前未发现
matrixPrimAndKruskal.kruskalAndPrim();
//获取边集数组
Edge[] edges1 = matrixPrimAndKruskal.getEdges();
System.out.println(Arrays.toString(edges1));
}
}5 인접 목록 가중치 그래프 구현여기서의 구현은 인접 목록을 기반으로 무방향 가중치 그래프를 구현하는 클래스를 구성할 수 있으며 깊이 우선 탐색 및 너비 우선 탐색을 위한 메서드를 제공하고 가장자리 집합을 얻는 메서드를 제공합니다. 배열을 제공하며 Prim과 Kruskal은 최소 스패닝 트리를 찾는 두 가지 방법입니다. 아아아아
위 내용은 Java에서 최소 스패닝 트리를 찾는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!