Python의 내장 힙을 구현하는 방법

1. 소개

우선순위 큐라고도 알려진 힙은 완전한 이진 트리이며 각 상위 노드의 값은 (의 값)보다 작거나 같습니다. 모든 하위 노드. 이 작업을 수행하기 위해 배열을 사용합니다. 0부터 계산하면 모든 k에 대해 heap[k] 가 있습니다. 비교를 위해 존재하지 않는 요소는 무한한 것으로 간주됩니다. 힙의 가장 흥미로운 특징은 가장 작은 요소가 항상 루트 노드인 heap[0]에 있다는 것입니다.

Python의 힙은 일반적으로 최소 힙으로, 대부분의 교과서에서는 최대 힙을 사용하므로 힙은 위에서 아래로, 왼쪽에서 오른쪽으로 표현되므로 목록과 매우 유사합니다. , 힙을 생성하려면 목록을 사용하여 []로 초기화하거나 heapify() 함수를 사용하여 목록을 힙으로 변환할 수 있습니다. 다음은 Python의 힙 관련 작업입니다. Python이 실제로 힙을 목록으로 처리한다는 것을 알 수 있습니다.

2. 힙 관련 작업

heapq.heappush(heap, item)

힙의 불변성을 유지하기 위해 항목의 값을 힙에 추가합니다. Python의 최소 힙 기능에 따라 관련 요소를 자동으로 교환하므로 힙의 루트 노드 요소가 하위 노드 요소보다 크지 않습니다.

원본 데이터는 힙

import heapq

h = [1, 2, 3, 5, 7]
heapq.heappush(h, 2)
print(h)
#输出
[1, 2, 2, 5, 7, 3]

작업 과정은 다음과 같습니다.

1. 2개의 요소를 추가한 후

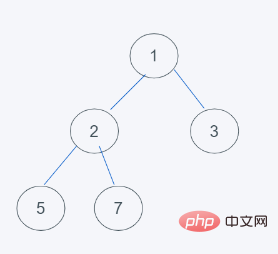
3. 최소 힙 특성을 충족하지 않으므로 3

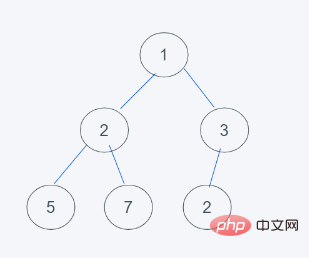
4로 교환합니다. 최소 힙 특성에 맞춰 교환이 종료되므로 결과는 [1, 2, 3, 5, 7, 3]

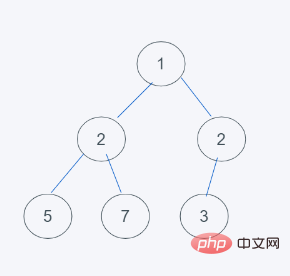원본 데이터는 힙이 아닙니다

import heapq

h = [5, 2, 1, 4, 7]
heapq.heappush(h, 2)
print(h)
#输出
[5, 2, 1, 4, 7, 2]

push 연산을 수행할 때 해당 요소가 힙이 아닌 경우 목록의 추가 방식에 따라 기본적으로 해당 요소가 추가되는 것을 알 수 있습니다.

heapq.heappop(heap)

힙의 가장 작은 요소를 팝하고 반환하여 힙 불변성을 유지합니다. 힙이 비어 있으면 IndexError를 발생시킵니다. heap[0] 을 사용하면 팝하지 않고 가장 작은 요소에만 액세스할 수 있습니다.

원본 데이터는 힙입니다

import heapq

h = [1, 2, 3, 5, 7]
heapq.heappop(h)
print(h)
#输出
[2, 5, 3, 7]

작업 과정은 다음과 같습니다.

1. 초기 상태

2.힙의 최상위 요소가 삭제되고 마지막 요소가 이동됩니다. 힙의 맨 위로

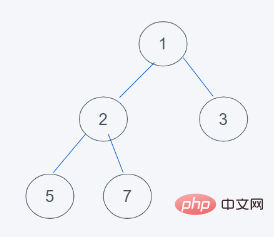
3. Basis Python의 최소 힙 특성에 따라 요소를 교환합니다. 7>2이므로 7과 2를 교환합니다

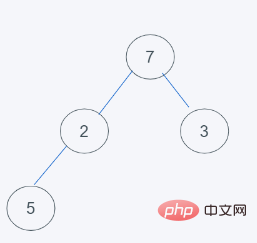
4. 힙이기 때문에 7과 5를 교환합니다

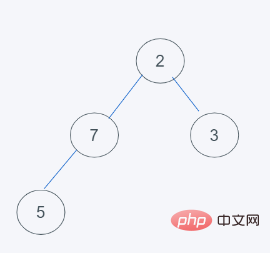
5 힙의 요구 사항을 충족합니다. 즉, 결과는 [2, 5, 3, 7]

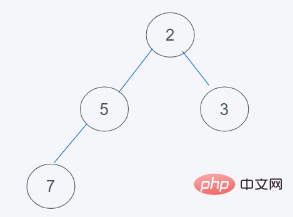원본 데이터가 힙이 아닙니다.

import heapq

h = [5, 2, 1, 4, 7]
heapq.heappop(h)
print(h)

[1, 2, 7, 4]

작업 프로세스는 다음과 같습니다.

1. 초기 상태는 분명히 힙의 속성을 충족하지 않습니다.

2. 최상위 요소(첫 번째 요소)를 제거하고 나머지 요소를 재정렬합니다. 힙에서

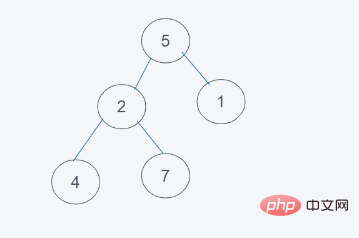
3. Python의 최소 힙 특성에 따라 2>1은 2와 1

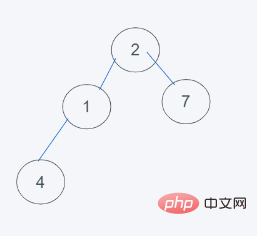
4을 교환하며 결과는 [1, 2, 7, 4]

heapq.heappushpop(heap, item)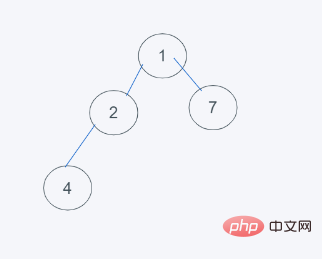

항목을 힙에 넣은 다음 팝업하고 힙 요소의 최소값을 반환합니다. 이 결합된 작업은 heappush()를 먼저 호출한 다음 heappop()을 호출하는 것보다 더 효율적으로 실행됩니다. 팝된 요소는 힙의 맨 위 또는 끝에 있어야 합니다. 즉, 요소가 삽입되고 가장 작은 요소가 비교되면 삽입된 요소가 항상 비교됩니다. 가 힙의 최상위 요소보다 크거나 같으면 힙은 변경되지 않습니다. 삽입된 요소가 힙의 최상위 요소보다 작으면 힙은 Python 힙의 최소 힙 특성에 따라 처리됩니다.

원본 데이터는 힙입니다

import heapq

h = [1, 2, 3, 5, 7]
min_data = heapq.heappushpop(h, 2)
print(min_data)
print(h)
#输出
1
[2, 2, 3, 5, 7]

작업 과정은 다음과 같습니다

1. 초기 상태

2.2번째 요소를 삽입합니다.

3.删除最小元素，刚好是堆顶元素1，并使用末尾元素2代替

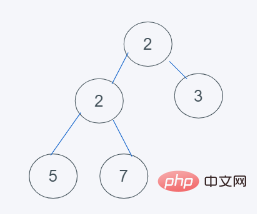
4.符合要求，即结果为[2, 2, 3, 5, 7]

原有数据不是堆

h = [5, 2, 1, 4, 7]
min_data = heapq.heappushpop(h, 2)
print(min_data)
print(h)
min_data = heapq.heappushpop(h, 6)
print(min_data)
print(h)

#输出
2
[5, 2, 1, 4, 7]
5
[1, 2, 6, 4, 7]

对于插入元素6的操作过程如下

1.初始状态

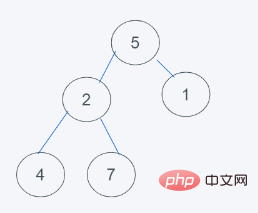
2.插入元素6之后

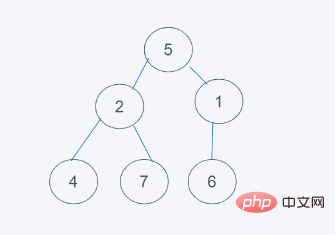
3.发现元素6大于堆顶元素5，弹出堆顶元素5，由堆尾元素6替换

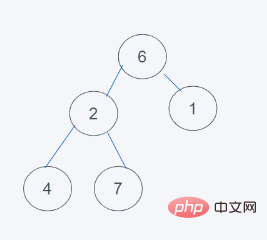
4.依据python的最小堆特性，元素6>元素1且元素6>元素2，但元素2>元素1， 交换6与1

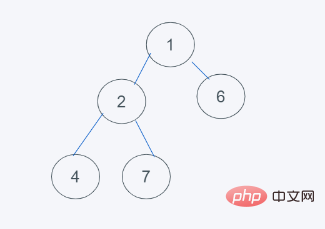
5.符合要求，则结果为[1, 2, 6, 4, 7]

由结果可以看出，当插入元素小于堆顶元素时，则堆不会发生改变，当插入元素大于堆顶元素时，则堆依据python堆的最小堆特性处理。

heapq.heapify(x)

将列表转换为堆。

h = [1, 2, 3, 5, 7]
heapq.heapify(h)
print(h)
h = [5, 2, 1, 4, 7]
heapq.heapify(h)
print(h)
#输出
[1, 2, 3, 5, 7]
[1, 2, 5, 4, 7]

会自动将列表依据python最小堆特性进行重新排列。

heapq.heapreplace(heap, item)

弹出并返回最小的元素，并且添加一个新元素item，这个单步骤操作比heappop()加heappush() 更高效。适用于堆元素数量固定的情况。

返回的值可能会比添加的 item 更大。 如果不希望如此，可考虑改用heappushpop()。 它的 push/pop 组合会返回两个值中较小的一个，将较大的值留在堆中。

import heapq

h = [1, 2, 3, 5, 7]
heapq.heapreplace(h, 6)
print(h)
h = [5, 2, 1, 4, 7]
heapq.heapreplace(h, 6)
print(h)
#输出
[2, 5, 3, 6, 7]
[1, 2, 6, 4, 7]

原有数据是堆

对于插入元素6的操作过程如下：

1.初始状态

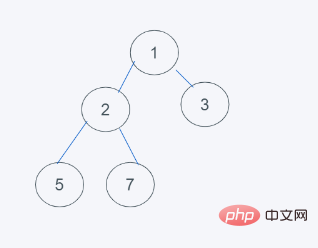
2.弹出最小元素，只能弹出堆顶或者堆尾的元素，很明显，最小元素是1，弹出1，插入元素是6，代替堆顶元素

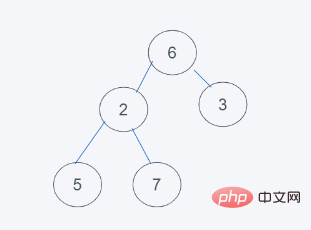
3.依据python堆的最小堆特性，6>2,交换6与2

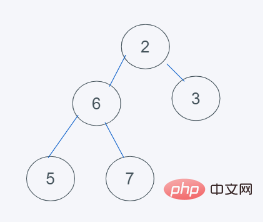
4.依据python堆的最小堆特性，6>5,交换6与5

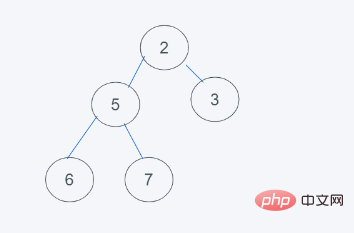
5.符合要求，则结果为[2, 5, 3, 6 ,7]

原有数据不是堆

对于插入元素6的操作过程如下：

1.初始状态

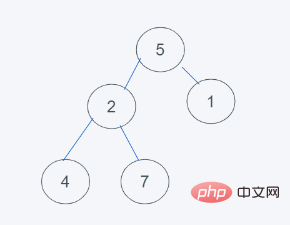
2.对于数据不为堆的情况下，默认移除第一个元素，这里就是元素5，然后插入元素6到堆顶

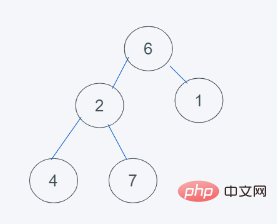
3.依据python的最小堆特性，元素6>1,交换元素6与1

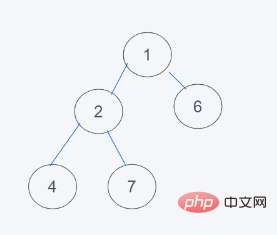
4.符合要求，即结果为[1, 2, 6, 4, 7

heapq.merge(*iterables, key=None, reverse=False)

将多个已排序的输入合并为一个已排序的输出（例如，合并来自多个日志文件的带时间戳的条目）。 返回已排序值的 iterator。注意需要是已排序完成的可迭代对象（默认为从小到大排序），当reverse为True时，则为从大到小排序。

heapq.nlargest(n, iterable, key=None)

从 iterable 所定义的数据集中返回前 n 个最大元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。

等价于: sorted(iterable, key=key, reverse=True)[:n]。

import time
import heapq

h = [1, 2, 3, 5, 7]

size = 1000000
start = time.time()
print(heapq.nlargest(3, h))
for i in range(size):
    heapq.nlargest(3, h)
print(time.time() - start)

start = time.time()
print(sorted(h, reverse=True)[:3:])
for i in range(size):
    sorted(h, reverse=True)[:3:]
print(time.time() - start)
#输出
[7, 5, 3]
1.6576552391052246
[7, 5, 3]
0.2772986888885498
[7, 5, 4]

由上述结构可见，heapq.nlargest与sorted(iterable, key=key, reverse=False)[:n]功能是类似的，但是性能方面还是sorted较为快速。

heapq.nsmallest(n, iterable, key=None)

从 iterable 所定义的数据集中返回前 n 个最小元素组成的列表。 如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。 等价于: sorted(iterable, key=key)[:n]。

import time
import heapq

h = [1, 2, 3, 5, 7]

size = 1000000
start = time.time()
print(heapq.nsmallest(3, h))
for i in range(size):
    heapq.nsmallest(2, h)
print(time.time() - start)

start = time.time()
print(sorted(h, reverse=False)[:3:])
for i in range(size):
    sorted(h, reverse=False)[:2:]
print(time.time() - start)
#输出
[1, 2, 3]
1.1738648414611816
[1, 2, 3]
0.2871997356414795

由上述结果可见，sorted的性能比后面两个函数都要好，但如果只是返回最大的或者最小的一个元素，则使用max和min最好。

3.堆排序

由于在python中堆的特性是最小堆，堆顶的元素始终是最小的，可以将序列转换成堆之后，再使用pop弹出堆顶元素来实现从小到大排序。具体实现如下：

from heapq import heappush, heappop, heapify


def heapsort(iterable):
    h = []
    for value in iterable:
        heappush(h, value)
    return [heappop(h) for i in range(len(h))]


def heapsort2(iterable):
    heapify(iterable)
    return [heappop(iterable) for i in range(len(iterable))]


data = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]

print(heapsort(data))
print(heapsort2(data))
#输出
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

4.堆中元素可以是元组形式，主要用于任务优先级

from heapq import heappush, heappop

h = []
heappush(h, (5, 'write code'))
heappush(h, (7, 'release product'))
heappush(h, (1, 'write spec'))
heappush(h, (3, 'create tests'))
print(h)
print(heappop(h))

[(1, 'write spec'), (3, 'create tests'), (5, 'write code'), (7, 'release product')]
(1, 'write spec')

上述操作流程如下：

1.当进行第一次push(5, ‘write code’)时

2.当进行第二次push(7, ‘release product’)时，符合堆的要求

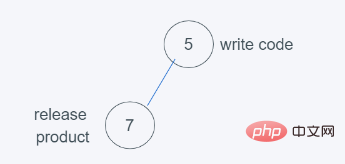
3.当进行第三次push(1, ‘write spec’)时，

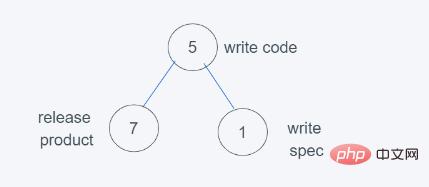
4.依据python的堆的最小堆特性，5>1 ，交换5和1

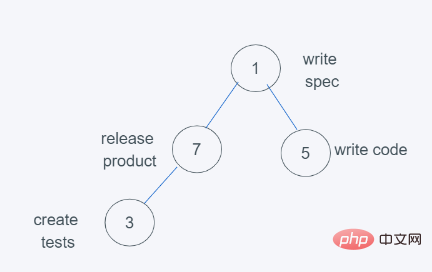
5.当进行最后依次push(3, ‘create tests’)时

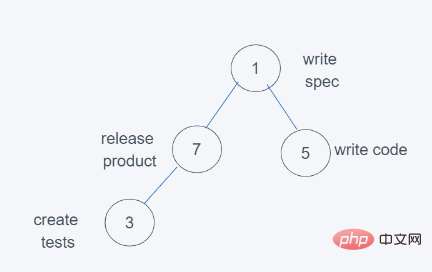
6.依据python堆的最小堆特性，7>3，交换7与3

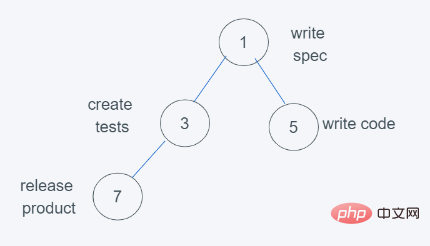
7.符合要求，因此结果为[(1, ‘write spec’), (3, ‘create tests’), (5, ‘write code’), (7, ‘release product’)],弹出元素则是堆顶元素，数字越小，优先级越大。

위 내용은 Python의 내장 힙을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!