Java 바이너리 검색 트리 추가, 삽입, 삭제 및 생성 예제에 대한 자세한 설명

①개념

이진 검색 트리는 이진 정렬 트리라고도 합니다. 이는 빈 트리**이거나 다음 속성을 가진 이진 트리입니다.

왼쪽 하위 트리가 비어 있지 않으면 값은 ​​왼쪽 하위 트리에 있는 모든 노드의 값이 루트 노드의 값보다 작습니다

오른쪽 하위 트리가 비어 있지 않으면 오른쪽 하위 트리에 있는 모든 노드의 값이 루트 노드의 값보다 큽니다

왼쪽 및 오른쪽 하위 트리도 각각 이진 검색 트리

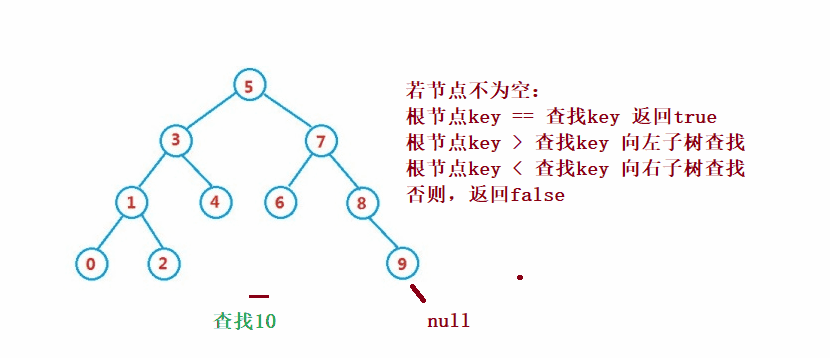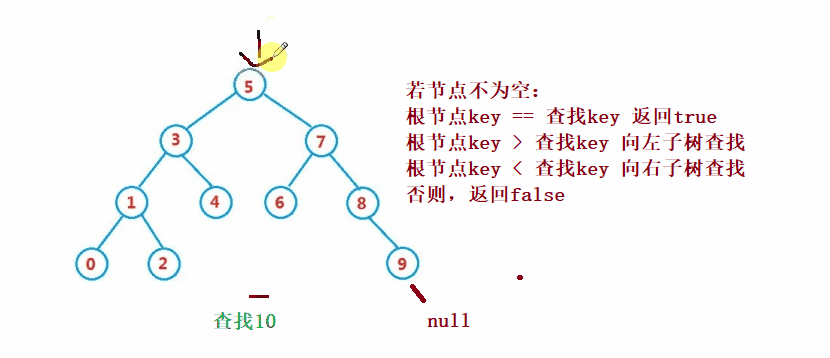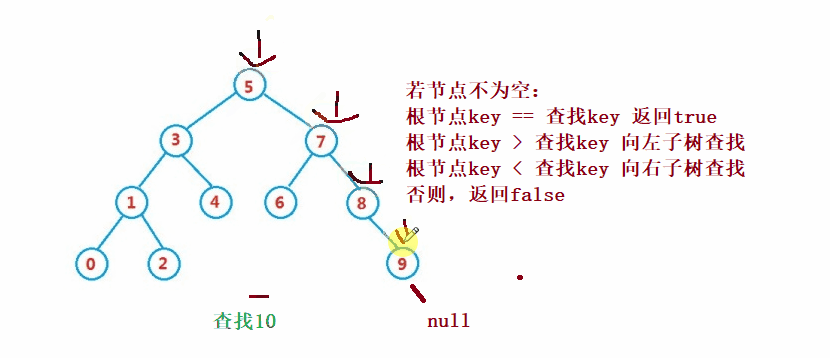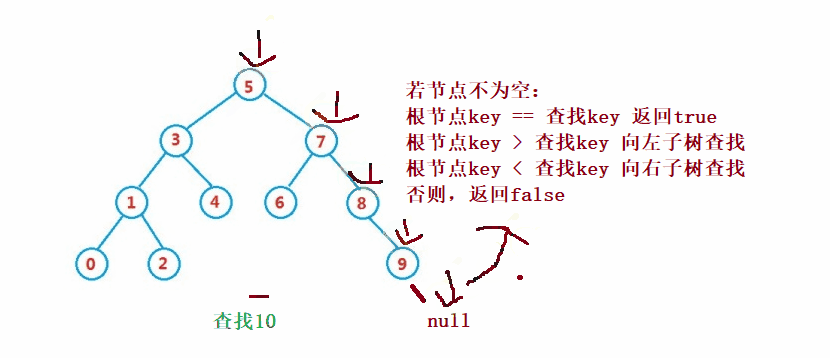
② 작업 - 찾기

이진 검색 트리의 검색은 이진 검색

public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

3과 유사합니다. 연산 - 삽입

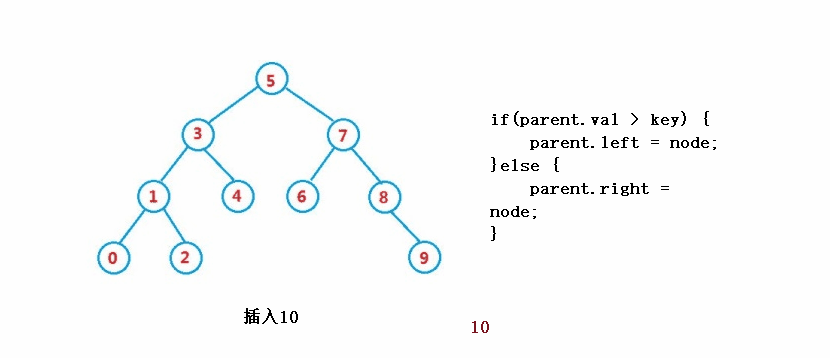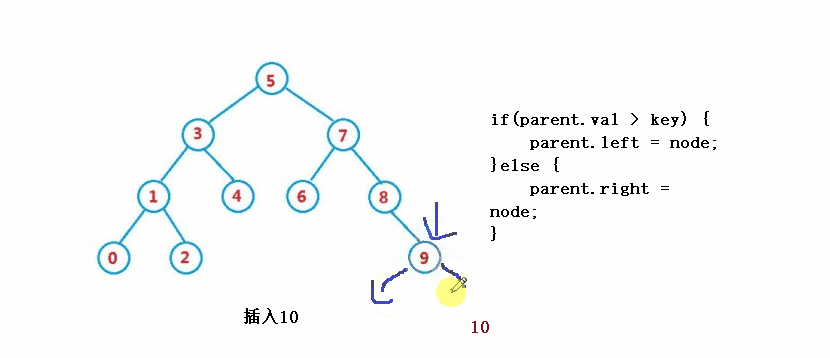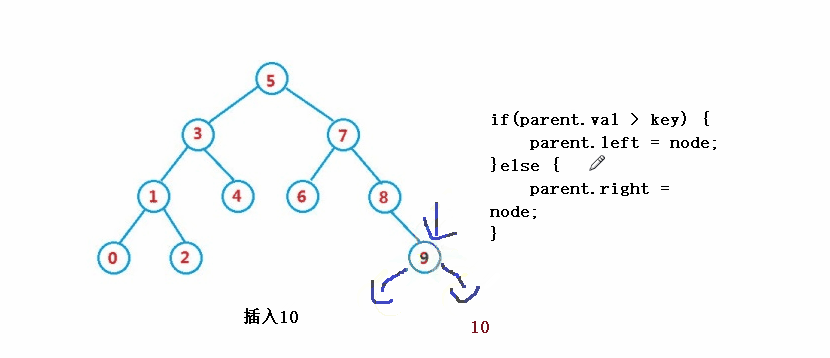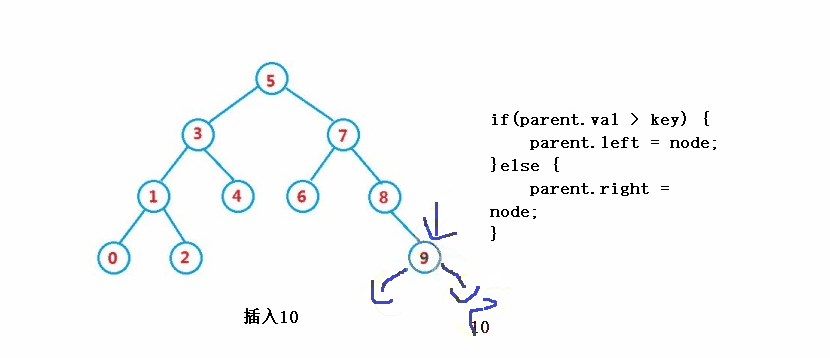
  public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }

④Operation-Delete

삭제 연산은 좀 더 복잡하지만 원리는 비교적 이해하기 쉽습니다

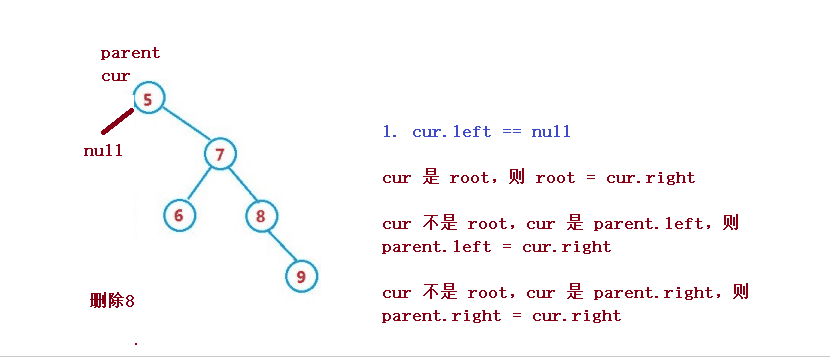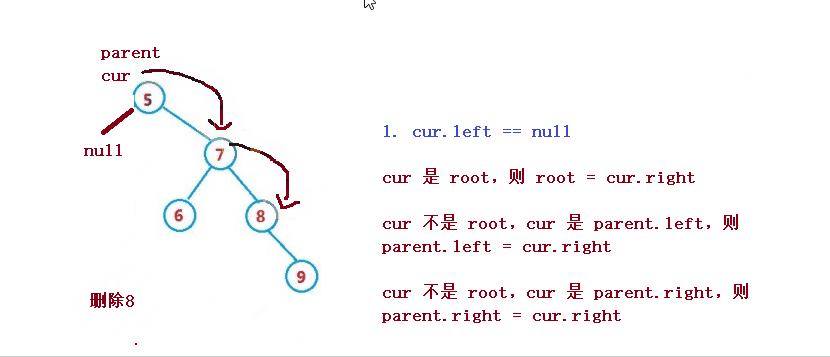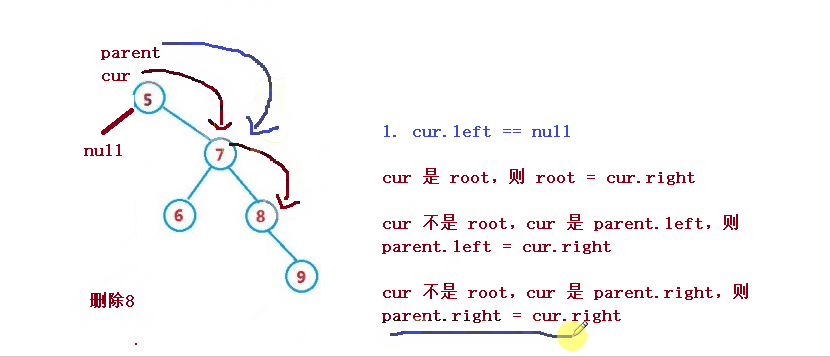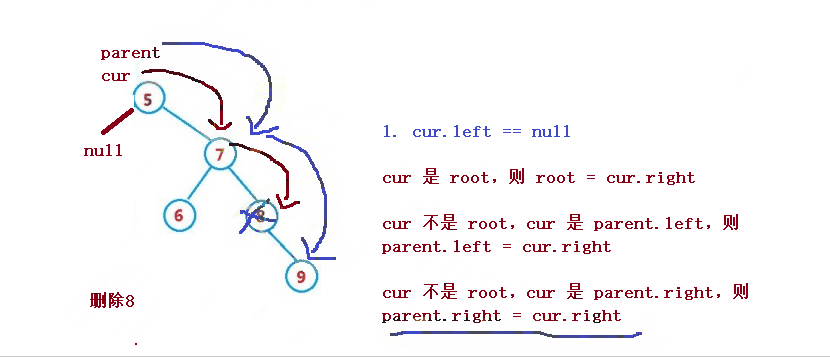
삭제할 노드가 cur라고 가정하면, 삭제될 노드의 상위 노드는 parent

1. cur.left == null

1. cur는 루트이고, root = cur.right

2. cur은 루트가 아니며, cur는 parent.left입니다. , parent.left = cur.right

3. cur는 루트가 아니며, cur는 parent.right이고, parent.right = cur.right

2. right == null

1. cur는 루트이고, root = cur .left

2. cur는 루트가 아니며, cur는 parent.left이고, parent.left = cur.left

3. cur는 parent.right이고 parent.right = cur.left

Second 이 상황은 반대 방향을 제외하면 첫 번째 상황과 동일합니다. 여기서는 더 이상 그릴 필요가 없습니다

3. cur.left != null && cur. right != null

삭제하려면 대체 방법을 사용해야 합니다. 즉, 오른쪽 하위 트리에서 중간 순서의 첫 번째 노드(가장 작은 키 코드)를 찾아 해당 값을 삭제된 노드에 채운 다음 노드의 삭제 문제를 처리합니다

왼쪽 또는 오른쪽 하위 트리가 모두 비어 있는 상황에서 노드를 삭제하면 트리 구조가 파괴되므로 희생양 방법을 사용하여 해결합니다. 실제 삭제 프로세스는 여전히 위의 두 가지 상황입니다. 여기서는 검색 바이너리 트리의 속성이 여전히 사용됩니다

public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
  public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

⑤성능 분석

먼저 검색해야 합니다. 검색 효율성은 이진 검색 트리의 각 작업 성능을 나타냅니다.

n개 노드가 있는 이진 검색 트리의 경우 각 요소를 검색할 확률이 동일하면 이진 검색 트리의 평균 검색 길이는 이진 검색 트리의 노드 깊이에 대한 함수입니다. 즉, 노드가 깊을수록 더 많은 비교가 발생합니다.

그러나 동일한 키 코드 세트에 대해 각 키 코드의 삽입 순서가 다르면 구조가 다른 이진 검색 트리를 얻을 수 있습니다.

최적의 경우 이진 검색 트리는 완전한 이진 트리이고, 평균 비교 횟수는

최악의 경우 이진 검색 트리는 단일 가지 트리로 변질되며 평균 비교 횟수는

⑥完整代码

public class TextDemo {
 
    public static class Node {
        public int val;
        public Node left;
        public Node right;
 
        public Node (int val) {
            this.val = val;
        }
    }
 
 
    public Node root;
 
    /**
     * 查找
     * @param key
     */
    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }
 
    /**
     *
     * @param key
     * @return
     */
    public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }
 
    public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
    public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
 
}

위 내용은 Java 바이너리 검색 트리 추가, 삽입, 삭제 및 생성 예제에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!