 기술 주변기기
기술 주변기기 일체 포함
일체 포함 새로운 연구는 한계를 극복하는 데 있어 신경망을 능가하는 양자 몬테카를로의 잠재력을 밝혔으며, Nature 하위 이슈에서는 최신 진행 상황을 자세히 설명합니다.
새로운 연구는 한계를 극복하는 데 있어 신경망을 능가하는 양자 몬테카를로의 잠재력을 밝혔으며, Nature 하위 이슈에서는 최신 진행 상황을 자세히 설명합니다.새로운 연구는 한계를 극복하는 데 있어 신경망을 능가하는 양자 몬테카를로의 잠재력을 밝혔으며, Nature 하위 이슈에서는 최신 진행 상황을 자세히 설명합니다.
4개월 후, ByteDance Research와 Peking University 물리학과 Chen Ji 연구 그룹의 또 다른 공동 작업이 최고의 국제 간행물에 게재되었습니다. Nature Communications: "Towards the ground state of Molecular via Diffusion Monte Carlo"라는 논문 on Neural Networks 》신경망과 확산 몬테카를로 방법을 결합하면 양자화학 관련 작업에서 신경망 방법의 계산 정확도, 효율성 및 시스템 규모가 크게 향상되어 최신 SOTA가 됩니다.

- 문서 링크:
https://www.nature.com/articles/s41467-023-37609-3 - 코드 주소:
https://github.com/bytedance/jaqmc
저자는 고정 노드 표면의 확산 몬테카를로 방법에 신경망 기반 시험 파동 함수를 적용합니다. (Diffusion Monte Carlo 또는 DMC)는 다양한 전자 특성을 가진 원자 및 분자 시스템을 정확하게 계산하는 데 사용됩니다.
확산 몬테카를로법은 분자와 물질의 바닥 상태 에너지를 정확하게 계산하기 위해 양자화학 분야에서 일반적으로 사용되는 방법 중 하나입니다. 저자들은 이를 확산 몬테카를로 방법과 결합하여 양자화학에서 신경망 SOTA 방법의 계산 정확도와 효율성을 크게 향상시켰습니다. 또한 저자는 경험적 선형 관계를 기반으로 한 외삽법도 제안했는데, 이는 분자 결합 에너지 계산을 크게 향상시켰습니다. 전반적으로, 이 계산 프레임워크는 양자 다체 문제를 해결하기 위한 고정밀 방법 역할을 하며, 화학 분자의 특성을 심층적으로 이해할 수 있는 보다 강력한 도구를 제공합니다.
신경망 기반 양자 몬테카를로 방법
2018년부터 여러 연구 그룹에서 변형 몬테카를로 방법(Variational Monte Carlo, 또는 VMC)에 신경망을 적용했습니다[1,2,3]. 신경망의 강력한 표현 능력의 도움으로 보다 정확한 분자 기저 상태 에너지를 얻을 수 있습니다. 본 연구가 2022년에 발표되었을 당시, 신경망 기반의 Variational Monte Carlo 방식의 SOTA 작업은 2019년 DeepMind가 제안한 FermiNet[2]으로, 더 작은 규모의 시스템에서도 매우 정확한 결과를 얻을 수 있었습니다. 그러나 변형 몬테카를로 방법의 정확성은 신경망의 표현 능력에 의해 제한되며, 대규모 시스템을 다룰 때 점점 더 명백한 정확성 문제가 발생할 것입니다. 또한 이러한 유형의 방법은 대규모 시스템을 처리할 때 매우 느리게 수렴되므로 컴퓨팅 리소스에 큰 문제를 야기합니다.
양자화학 분야의 고전적인 고정밀 알고리즘 중 하나로 확산 몬테카를로법은 높은 정확성, 우수한 병렬성 등의 좋은 특성을 가지며 대규모 계산에 적합합니다. 또한 확산 몬테카를로(Diffusion Monte Carlo)는 신경망 표현 능력의 한계를 극복하고 투영 알고리즘을 사용하여 변이 몬테카를로 방법의 정확도를 뛰어넘을 수 있습니다.
이 작업에서 저자는 SOTA의 신경망(FermiNet)을 시험 파동 함수로 확산 몬테 카를로 방법과 결합합니다. 새로운 계산 방법은 FermiNet에 비해 정확도를 크게 향상시키고 필요한 계산 단계 수를 줄입니다. 이 작업에서 설계 및 구현된 확산 몬테카를로 소프트웨어는 신경망 친화적, GPU 친화적, 병렬 친화적입니다. 광범위한 신경망 파동 기능과 결합하여 정확도와 효율성을 자동으로 향상시킬 수 있습니다.
계산 결과1. Atoms
대규모 분자계에서 양자 몬테카를로 계산을 하기 위해 신경망을 사용하는 경우, 컴퓨팅 파워의 한계로 인해 신경망의 표현 능력이 사용도 제한됩니다. 특정 제한사항. 이 시나리오를 시뮬레이션하기 위해 저자는 두 개의 신경망 계층만 사용하여 두 번째와 세 번째 행의 원자를 연구했습니다. 계산 결과는 시스템이 커질수록 변형 몬테카를로 방법의 정확도가 점점 더 나빠지는 반면, 확산 몬테카를로 방법에 의한 정확도 향상은 점점 더 분명해짐을 보여줍니다.

2. 분자
저자는 또한 질소 분자, 시클로부타디엔, 이중 물 분자를 포함한 일련의 분자 시스템에서 신경망 기반 확산 몬테카를로 방법의 유효성을 검증했습니다. 테스트한 모든 시스템에서 계산 정확도가 크게 향상되었습니다.
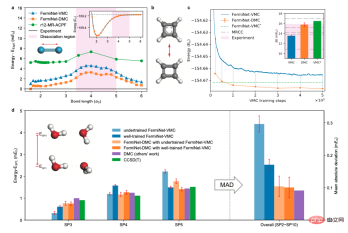
3. 벤젠 고리와 디페닐 고리
이 작품이 출판되기 전에는 양자화학 분야에서 변이형 몬테카를로를 기반으로 한 신경망 파동 함수 방법은 30개 정도만 다루었습니다. 전자 이하 소분자. 이 연구는 처음으로 42~84개의 전자를 가진 시스템, 즉 벤젠 고리와 비페닐 고리에 신경망 파동 함수 방법을 적용했습니다. 계산 결과는 확산 몬테카를로 방법이 변형 몬테카를로 방법보다 정확도가 훨씬 우수하며, 한 자릿수 더 적은 계산 단계로 동일하거나 더 나은 정확도를 달성할 수 있음을 보여줍니다.
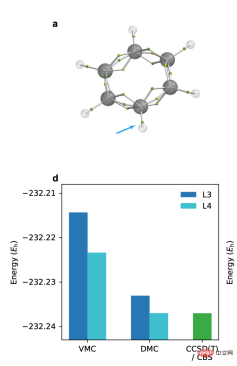

4. 선형 관계 및 외삽 방법
저자가 신경망의 다양한 훈련 단계에 해당하는 에너지를 조사한 결과 여러 시스템에서 변형이 발견되었습니다. 몬테카를로와 확산의 결과 몬테카를로에는 경험적인 선형 관계가 있습니다(아래 왼쪽 그림). 이 선형 관계를 사용하여 비페닐 고리의 해리 에너지 계산을 추정하면 계산 정확도가 크게 향상되고 화학 실험과 일치하는 결과를 얻을 수 있습니다(아래 오른쪽 그림).

결론 및 전망
이 연구는 신경망을 기반으로 한 확산 몬테카를로 방법이 변형 몬테카를로 방법보다 정확성과 효율성 모두에서 우수하다는 것을 보여줍니다. 저자의 오픈 소스 확산 몬테 카를로 코드는 양자 화학 분야의 끊임없이 혁신적인 신경망[4,5]과 빠르게 결합되어 연구 커뮤니티에 힘을 실어줄 수 있습니다. 또한, 확산 몬테 카를로 방법은 실제 고체를 다루는 주기 신경망[6] 및 유사 전위 신경망[7]과 같은 일련의 방법과 결합하여 해당 작업에 대한 컴퓨팅 효과를 향상시킬 수도 있습니다.
위 내용은 새로운 연구는 한계를 극복하는 데 있어 신경망을 능가하는 양자 몬테카를로의 잠재력을 밝혔으며, Nature 하위 이슈에서는 최신 진행 상황을 자세히 설명합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM
Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM과학자들은 C. el 그러나 중요한 질문이 발생합니다. 새로운 AI S와 함께 효과적으로 작동하도록 우리 자신의 신경망을 어떻게 조정합니까?
 새로운 Google 유출은 Gemini AI의 구독 변경을 보여줍니다Apr 27, 2025 am 11:08 AM
새로운 Google 유출은 Gemini AI의 구독 변경을 보여줍니다Apr 27, 2025 am 11:08 AMGoogle의 Gemini Advanced : 수평선의 새로운 가입 계층 현재 Gemini Advanced에 액세스하려면 $ 19.99/월 Google One AI Premium Plan이 필요합니다. 그러나 Android Authority 보고서는 다가오는 변경 사항을 암시합니다. 최신 Google p. 내 코드
 데이터 분석 가속이 AI의 숨겨진 병목 현상을 해결하는 방법Apr 27, 2025 am 11:07 AM
데이터 분석 가속이 AI의 숨겨진 병목 현상을 해결하는 방법Apr 27, 2025 am 11:07 AM고급 AI 기능을 둘러싼 과대 광고에도 불구하고 Enterprise AI 배포 내에서 상당한 도전 과제 : 데이터 처리 병목 현상. CEO는 AI 발전을 축하하는 동안 엔지니어는 느린 쿼리 시간, 과부하 파이프 라인,
 Markitdown MCP는 모든 문서를 Markdowns로 변환 할 수 있습니다!Apr 27, 2025 am 09:47 AM
Markitdown MCP는 모든 문서를 Markdowns로 변환 할 수 있습니다!Apr 27, 2025 am 09:47 AM문서 처리는 더 이상 AI 프로젝트에서 파일을 여는 것이 아니라 혼돈을 명확하게 전환하는 것입니다. PDF, PowerPoint 및 Word와 같은 문서는 모든 모양과 크기로 워크 플로우를 범람합니다. 구조화 된 검색
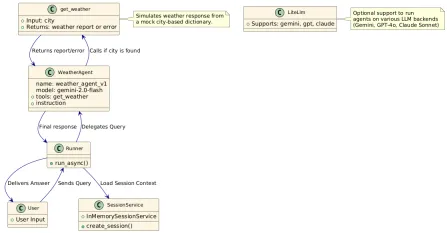 빌딩 에이전트에 Google ADK를 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:42 AM
빌딩 에이전트에 Google ADK를 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:42 AMGoogle의 에이전트 개발 키트 (ADK)의 전력을 활용하여 실제 기능을 갖춘 지능형 에이전트를 만듭니다! 이 튜토리얼은 Gemini 및 GPT와 같은 다양한 언어 모델을 지원하는 ADK를 사용하여 대화 에이전트를 구축하는 것을 안내합니다. w
 효과적인 문제 해결을 위해 LLM을 통해 SLM 사용 - 분석 VidhyaApr 27, 2025 am 09:27 AM
효과적인 문제 해결을 위해 LLM을 통해 SLM 사용 - 분석 VidhyaApr 27, 2025 am 09:27 AM요약: SLM (Small Language Model)은 효율성을 위해 설계되었습니다. 자원 결핍, 실시간 및 개인 정보 보호 환경에서 LLM (Large Language Model)보다 낫습니다. 초점 기반 작업, 특히 도메인 특이성, 제어 성 및 해석 성이 일반적인 지식이나 창의성보다 더 중요합니다. SLM은 LLM을 대체하지는 않지만 정밀, 속도 및 비용 효율성이 중요 할 때 이상적입니다. 기술은 더 적은 자원으로 더 많은 것을 달성하는 데 도움이됩니다. 그것은 항상 운전자가 아니라 프로모터였습니다. 증기 엔진 시대부터 인터넷 버블 시대에 이르기까지 기술의 힘은 문제를 해결하는 데 도움이되는 정도입니다. 인공 지능 (AI) 및보다 최근에 생성 AI가 예외는 아닙니다.
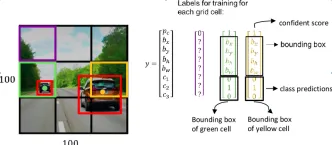 컴퓨터 비전 작업에 Google Gemini 모델을 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:26 AM
컴퓨터 비전 작업에 Google Gemini 모델을 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:26 AM컴퓨터 비전을위한 Google Gemini의 힘을 활용 : 포괄적 인 가이드 주요 AI 챗봇 인 Google Gemini는 강력한 컴퓨터 비전 기능을 포괄하기 위해 대화를 넘어서 기능을 확장합니다. 이 안내서는 사용 방법에 대해 자세히 설명합니다
 Gemini 2.0 Flash vs O4-Mini : Google은 OpenAi보다 더 잘할 수 있습니까?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini : Google은 OpenAi보다 더 잘할 수 있습니까?Apr 27, 2025 am 09:20 AM2025 년의 AI 환경은 Google의 Gemini 2.0 Flash와 Openai의 O4-Mini가 도착하면서 전기가 전환됩니다. 이 최첨단 모델은 몇 주 간격으로 발사되어 비슷한 고급 기능과 인상적인 벤치 마크 점수를 자랑합니다. 이 심층적 인 비교


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

SecList
SecLists는 최고의 보안 테스터의 동반자입니다. 보안 평가 시 자주 사용되는 다양한 유형의 목록을 한 곳에 모아 놓은 것입니다. SecLists는 보안 테스터에게 필요할 수 있는 모든 목록을 편리하게 제공하여 보안 테스트를 더욱 효율적이고 생산적으로 만드는 데 도움이 됩니다. 목록 유형에는 사용자 이름, 비밀번호, URL, 퍼징 페이로드, 민감한 데이터 패턴, 웹 셸 등이 포함됩니다. 테스터는 이 저장소를 새로운 테스트 시스템으로 간단히 가져올 수 있으며 필요한 모든 유형의 목록에 액세스할 수 있습니다.

mPDF
mPDF는 UTF-8로 인코딩된 HTML에서 PDF 파일을 생성할 수 있는 PHP 라이브러리입니다. 원저자인 Ian Back은 자신의 웹 사이트에서 "즉시" PDF 파일을 출력하고 다양한 언어를 처리하기 위해 mPDF를 작성했습니다. HTML2FPDF와 같은 원본 스크립트보다 유니코드 글꼴을 사용할 때 속도가 느리고 더 큰 파일을 생성하지만 CSS 스타일 등을 지원하고 많은 개선 사항이 있습니다. RTL(아랍어, 히브리어), CJK(중국어, 일본어, 한국어)를 포함한 거의 모든 언어를 지원합니다. 중첩된 블록 수준 요소(예: P, DIV)를 지원합니다.

WebStorm Mac 버전
유용한 JavaScript 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경






