Java에서 무방향 그래프를 구현하는 방법은 무엇입니까?

기본 개념

그래프 정의

A 그래프는 VV A 바이너리의 순서 없는 요소 쌍으로 구성된 점 집합 V={v_i}과 집합 E={e_k}으로 구성됩니다. 그룹, G=(V,E)로 기록되며, V의 v_i 요소를 정점이라고 하며 E의 요소 e_k를 모서리라고 합니다.

V의 두 점 u, v에 대해 모서리(u, v)가 E에 속하면 두 점 u와 v는 인접하다고 하며 u와 v를 모서리(u, v)의 끝점이라고 합니다. V).

m(G)=|E|를 사용하여 그래프 G의 모서리 수를 나타내고 n(G)=|V|를 사용하여 그래프 G의 정점 수를 나타낼 수 있습니다.

무방향 그래프의 정의

E에 있는 임의의 간선(vi, vj)에 대해 간선(vi, vj)의 끝점이 순서가 없으면 무방향 간선입니다. 이때 그래프 G를 무방향 간선이라고 합니다. 그래프. 무방향 그래프는 가장 단순한 그래프 모델입니다. 다음 그림은 동일한 무방향 그래프를 보여줍니다. 정점은 원으로 표시되고 모서리는 화살표 없이 정점 간의 연결입니다("알고리즘 4판"의 그림). 무방향 그래프 API

무방향 그래프의 경우 정점 수, 가장자리 수, 각 정점의 인접한 정점 및 가장자리 추가 작업에 관심이 있으므로 인터페이스는 다음과 같습니다.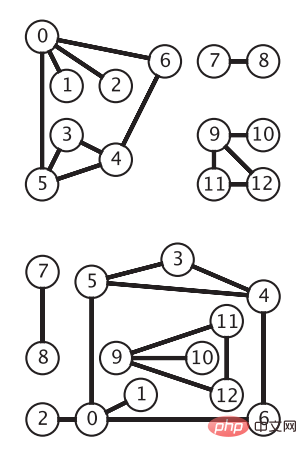

package com.zhiyiyo.graph;

/**
 * 无向图
 */
public interface Graph {
    /**
     * 返回图中的顶点数
     */
    int V();

    /**
     * 返回图中的边数
     */
    int E();

    /**
     * 向图中添加一条边
     * @param v 顶点 v
     * @param w 顶点 w
     */
    void addEdge(int v, int w);

    /**
     * 返回所有相邻顶点
     * @param v 顶点 v
     * @return 所有相邻顶点
     */
    Iterable<Integer> adj(int v);
}

무방향 그래프 구현 graph

인접 행렬

그래프를 표현하기 위해 행렬을 사용하는 것은 그래프의 속성과 응용을 연구하는 데 더 편리합니다. 가중치 행렬, ​​인접 행렬 등 다양한 그래프 표현이 있습니다. 인접 행렬.

그래프 G=(V,E), |V|=n에 대해 행렬 A=(a

ij

)

n×n

을 구성합니다. 여기서:

이 호출됩니다. 행렬 A는 그래프 G의 인접 행렬입니다.

A[i][j] = true일 때 2차원 부울 배열 A를 사용하여 인접 행렬을 구현할 수 있다는 것을 정의에서 볼 수 있습니다. , 이는 정점 i와 j가 인접해 있음을 나타냅니다.

n개의 정점이 있는 그래프 G의 경우 인접 행렬이 소비하는 공간은 ​​n² 부울 값이며, 이는 희소 그래프의 경우 많은 낭비를 초래합니다. , 소비되는 공간은 천문학적 수치가 될 것입니다. 동시에 그래프가 특별하고 자체 루프와 평행 모서리를 갖는 경우 인접 행렬 표현은 무력합니다. "알고리즘"은 다음 두 가지 상황을 보여줍니다.

A 来实现邻接矩阵，当 A[i][j] = true 时说明顶点 i 和 j 相邻。

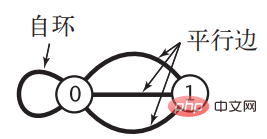
对于 n个顶点的图 G，邻接矩阵需要消耗的空间为 n²个布尔值的大小，对于稀疏图来说会造成很大的浪费，当顶点数很大时所消耗的空间会是个天文数字。同时当图比较特殊，存在自环以及平行边时，邻接矩阵的表示方式是无能为力的。《算法》中给出了存在这两种情况的图：

边的数组

对于无向图，我们可以实现一个类 Edge，里面只用两个实例变量用来存储两个顶点 u和 v，接着在一个数组里面保存所有 EdgeArray of edge

무방향 그래프의 경우 두 개의 인스턴스 변수만 사용하여 두 개의 정점 u와 v를 저장한 다음 모두 저장하는 Edge 클래스를 구현할 수 있습니다. 배열의 Edge. 여기에는 큰 문제가 있습니다. 즉, 정점 v의 모든 인접한 정점을 얻으려면 전체 배열을 순회해야 합니다. 인접한 정점을 얻는 것은 매우 일반적인 작업이므로 시간 복잡도는 O(|E|)입니다. , 이런 표현도 안 돼요.

인접 목록 배열

꼭지점을 값 범위 0∼|V|−1의 정수로 표현하면 길이가 |V|인 배열의 인덱스를 사용하여 각 꼭지점을 나타낼 수 있습니다. 배열 요소는 인덱스로 표시되는 꼭지점에 인접한 다른 꼭지점을 보유하는 연결 목록으로 설정됩니다. 그림 1의 무방향 그래프는 아래 그림과 같은 인접 리스트 배열로 표현할 수 있다.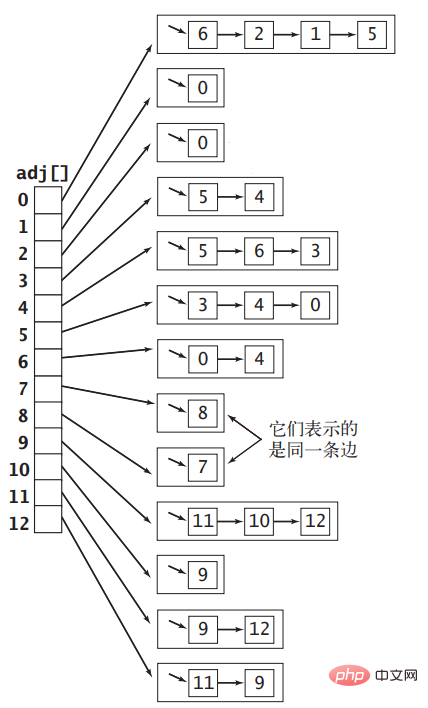

인접 리스트를 이용하여 무방향 그래프를 구현하는 코드는 다음과 같다. 인접 리스트의 각 연결 리스트는 다음과 같다. 배열은 정점에 인접한 정점을 저장하므로 그래프에 가장자리를 추가할 때 배열의 두 연결 목록에 노드를 추가해야 합니다.

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;

/**
 * 使用邻接表实现的无向图
 */
public class LinkGraph implements Graph {
    private final int V;
    private int E;
    private LinkStack<Integer>[] adj;

    public LinkGraph(int V) {
        this.V = V;
        adj = (LinkStack<Integer>[]) new LinkStack[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new LinkStack<>();
        }
    }

    @Override
    public int V() {
        return V;
    }

    @Override
    public int E() {
        return E;
    }

    @Override
    public void addEdge(int v, int w) {
        adj[v].push(w);
        adj[w].push(v);
        E++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

여기서 사용된 스택 코드는 스택의 구현입니다. 이 블로그의 일부가 아닙니다. 핵심 사항이므로 여기서는 너무 많이 설명하지 않겠습니다.

package com.zhiyiyo.collection.stack;

import java.util.EmptyStackException;
import java.util.Iterator;

/**
 * 使用链表实现的堆栈
 */
public class LinkStack<T> {
    private int N;
    private Node first;

    public void push(T item) {
        first = new Node(item, first);
        N++;
    }

    public T pop() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        N--;
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    public Iterator<T> iterator() {
        return new ReverseIterator();
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }


    private class ReverseIterator implements Iterator<T> {
        private Node node = first;

        @Override
        public boolean hasNext() {
            return node != null;
        }

        @Override
        public T next() {
            T item = node.item;
            node = node.next;
            return item;
        }

        @Override
        public void remove() {
        }
    }
}

Traversal of undirected graph

다음 그림이 주어지면 이제 각 정점에서 정점 0까지의 경로를 찾아야 합니다. 방법 이것을 달성? 또는 간단히 말해서 정점 0과 4가 주어지면 정점 0에서 시작하여 정점 4에 도달할 수 있는지 여부를 결정해야 합니다. 이를 달성하는 방법은 무엇입니까? 이를 위해서는 깊이 우선 검색과 너비 우선 검색이라는 두 가지 그래프 순회 방법을 사용해야 합니다.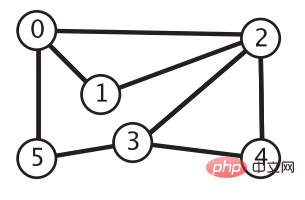

🎜이 두 가지 순회 방법을 소개하기 전에 먼저 위의 문제를 해결하기 위해 구현해야 하는 API를 제공하겠습니다. 🎜

package com.zhiyiyo.graph;

public interface Search {
    /**
     * 起点 s 和 顶点 v 之间是否连通
     * @param v 顶点 v
     * @return 是否连通
     */
    boolean connected(int v);

    /**
     * 返回与顶点 s 相连通的顶点个数（包括 s）
     */
    int count();

    /**
     * 是否存在从起点 s 到顶点 v 的路径
     * @param v 顶点 v
     * @return 是否存在路径
     */
    boolean hasPathTo(int v);

    /**
     * 从起点 s 到顶点 v 的路径，不存在则返回 null
     * @param v 顶点 v
     * @return 路径
     */
    Iterable<Integer> pathTo(int v);
}

深度优先搜索

深度优先搜索的思想类似树的先序遍历。我们从顶点 0 开始，将它的相邻顶点 2、1、5 加到栈中。接着弹出栈顶的顶点 2，将它相邻的顶点 0、1、3、4 添加到栈中，但是写到这你就会发现一个问题：顶点 0 和 1明明已经在栈中了，如果还把他们加到栈中，那这个栈岂不是永远不会变回空。所以还需要维护一个数组 boolean[] marked，当我们将一个顶点 i 添加到栈中时，就将 marked[i] 置为 true，这样下次要想将顶点 i 加入栈中时，就得先检查一个 marked[i] 是否为 true，如果为 true 就不用再添加了。重复栈顶节点的弹出和节点相邻节点的入栈操作，直到栈为空，我们就完成了顶点 0 可达的所有顶点的遍历。

为了记录每个顶点到顶点 0 的路径，我们还需要一个数组 int[] edgeTo。每当我们访问到顶点 u 并将其一个相邻顶点 i 压入栈中时，就将 edgeTo[i] 设置为 u，说明要想从顶点i 到达顶点 0，需要先回退顶点 u，接着再从顶点 edgeTo[u] 处获取下一步要回退的顶点直至找到顶点 0。

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;


public class DepthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public DepthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        dfs();
    }

    /**
     * 递归实现的深度优先搜索
     *
     * @param v 顶点 v
     */
    private void dfs(int v) {
        marked[v] = true;
        N++;
        for (int i : graph.adj(v)) {
            if (!marked[i]) {
                edgeTo[i] = v;
                dfs(i);
            }
        }
    }

    /**
     * 堆栈实现的深度优先搜索
     */
    private void dfs() {
        Stack<Integer> vertexes = new LinkStack<>();
        vertexes.push(s);
        marked[s] = true;

        while (!vertexes.isEmpty()) {
            Integer v = vertexes.pop();
            N++;

            // 将所有相邻顶点加到堆栈中
            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    vertexes.push(i);
                }
            }
        }
    }

    @Override
    public boolean connected(int v) {
        return marked[v];
    }

    @Override
    public int count() {
        return N;
    }

    @Override
    public boolean hasPathTo(int v) {
        return connected(v);
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new LinkStack<>();

        int vertex = v;
        while (vertex != s) {
            path.push(vertex);
            vertex = edgeTo[vertex];
        }

        path.push(s);
        return path;
    }
}

广度优先搜索

广度优先搜索的思想类似树的层序遍历。与深度优先搜索不同，从顶点 0 出发，广度优先搜索会先处理完所有与顶点 0 相邻的顶点 2、1、5 后，才会接着处理顶点 2、1、5 的相邻顶点。这个搜索过程就是一圈一圈往外扩展、越走越远的过程，所以可以用来获取顶点 0 到其他节点的最短路径。只要将深度优先搜索中的堆换成队列，就能实现广度优先搜索：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;

public class BreadthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public BreadthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        bfs();
    }

    private void bfs() {
        LinkQueue<Integer> queue = new LinkQueue<>();
        marked[s] = true;
        queue.enqueue(s);

        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            N++;

            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    queue.enqueue(i);
                }
            }
        }
    }
}

队列的实现代码如下：

package com.zhiyiyo.collection.queue;


import java.util.EmptyStackException;


public class LinkQueue<T> {
    private int N;
    private Node first;
    private Node last;

    public void enqueue(T item) {
        Node node = new Node(item, null);
        if (++N == 1) {
            first = node;
        } else {
            last.next = node;
        }
        last = node;
    }

    public T dequeue() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        if (--N == 0) {
            last = null;
        }
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

위 내용은 Java에서 무방향 그래프를 구현하는 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!